
。1 如果t-1期末,发生了上述第二种情况,即Y的 值小于其均衡值,则期末Y的变化往往会比第 一种情形下Y的变化大一些; ● 反之,如果t-1期末Y的值大于其均衡值,则期 末Y的变化往往会小于第一种情形下的△Yt。 ·可见,如果Yoo+o1X+Ht正确地提示了X与Y 间的长期稳定的“均衡关系”,则意味着Y对 其均衡点的偏离从本质上说是“临时性”的。 一个重要的假设就是:随机扰动项必须是平稳 序列。如果有随机性趋势(上升或下降) 则会导致Y对其均衡点的任何偏离都会被长期 累积下来而不能被消除
• 如果t-1期末,发生了上述第二种情况,即Y的 值小于其均衡值,则t期末Y的变化往往会比第 一种情形下Y的变化大一些; • 反之,如果t-1期末Y的值大于其均衡值,则t期 末Y的变化往往会小于第一种情形下的Yt。 • 可见,如果Yt =0+1Xt+t正确地提示了X与Y 间的长期稳定的“均衡关系” ,则意味着Y对 其均衡点的偏离从本质上说是“临时性”的。 • 一个重要的假设就是:随机扰动项t必须是平稳 序列。如果t有随机性趋势(上升或下降), 则会导致Y对其均衡点的任何偏离都会被长期 累积下来而不能被消除

式Yo+oX+u中的随机扰动项也被称为非均 衡误差(disequilibrium error),它是变量X 与Y的一个线性组合: 4,=Y-a0-CX, ·如果X与Y间的长期均衡关系正确,该式表述的非 均衡误差应是一平稳时间序列,并且具有零期望值, 即是具有0均值的(0)序列。 ·非稳定的时间序列,它们的线性组合也可能成为 平稳的。称变量X与Y是协整的(cointegrated)
• 式Yt =0+1Xt+t中的随机扰动项也被称为非均 衡误差(disequilibrium error),它是变量X 与Y的一个线性组合: t = Yt −0 −1 Xt • 如果X与Y间的长期均衡关系正确,该式表述的非 均衡误差应是一平稳时间序列,并且具有零期望值, 即是具有0均值的I(0)序列。 • 非稳定的时间序列,它们的线性组合也可能成为 平稳的。称变量X与Y是协整的(cointegrated)

3、协整 ·如果序列{X1t,X2t,Xkt}都是d阶单整,存在向量 0=(c1,2,k),使得Z=0XT、I(d-b) 其中,b>0,X=(X1t,X2t,Xk)T,则认为序列 {X1t,X2t,Xkt}是(d,b)阶协整,记为XCI(d,b), a为协整向量(cointegrated vector)。 ·如果两个变量都是单整变量,只有当它们的单整 阶数相同时,才可能协整:如果它们的单整阶数 不相同,就不可能协整
3、协整 • 如果序列{X1t,X2t,.,Xkt}都是d阶单整,存在向量 =(1,2,.,k),使得Zt =X T ~ I(d-b), 其中,b>0,X=(X1t,X2t,.,Xkt) T,则认为序列 {X1t,X2t,.,Xkt}是(d,b)阶协整,记为Xt~CI(d,b), 为协整向量(cointegrated vector)。 • 如果两个变量都是单整变量,只有当它们的单整 阶数相同时,才可能协整;如果它们的单整阶数 不相同,就不可能协整
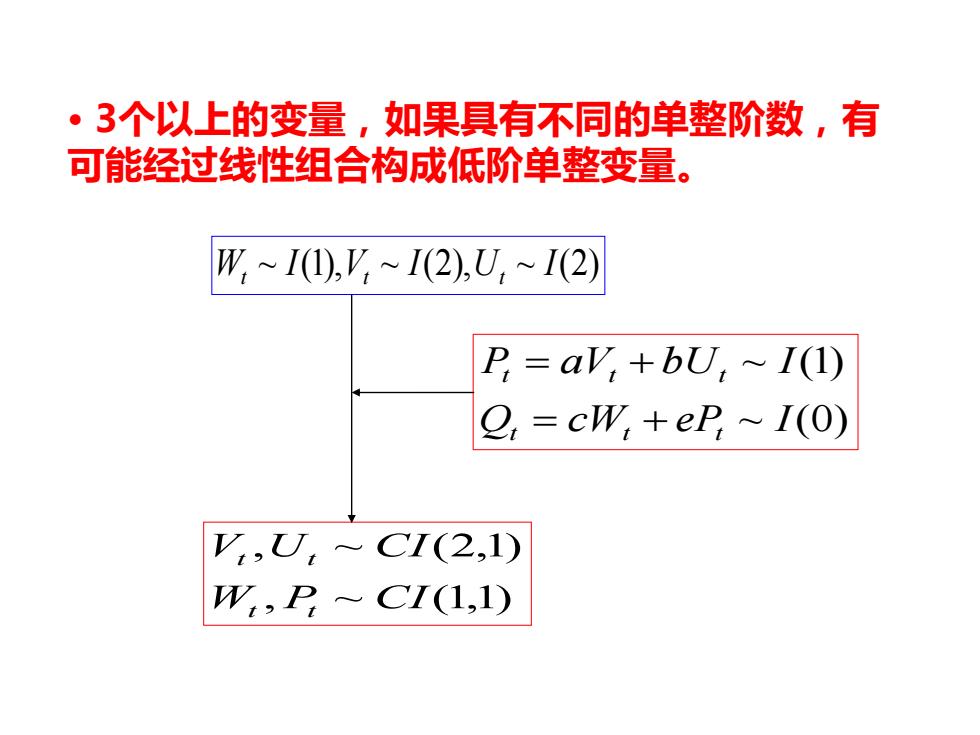
·3个以上的变量,如果具有不同的单整阶数,有 可能经过线性组合构成低阶单整变量。 W,~I(I),V~I(2),U,~1I(2) P=av,+bU ~I(1) 2,=cW,+eP~I(0) V,U,~CI(2,1) W,P~CI(1,1)
• 3个以上的变量,如果具有不同的单整阶数,有 可能经过线性组合构成低阶单整变量。 W ~ I(1),V ~ I(2),U ~ I(2) t t t ~ (0) ~ (1) Q cW eP I P aV bU I t t t t t t = + = + , ~ (1,1) , ~ (2,1) W P CI V U CI t t t t

(d,d)阶协整是一类非常重要的协整关系, 它的经济意义在于:两个变量,虽然它们具有 各自的长期波动规律,但是如果它们是(d,d) 阶协整的,则它们之间存在着一个长期稳定的 比例关系。 例如,中国CPC和GDPPC,它们各自都是2阶单整,如果 它们是(2,2)阶协整,说明它们之间存在着一个长期稳 定的比例关系,从计量经济学模型的意义上讲,建立 如下居民人均消费函数模型是合理的。 CPC do+a GDPPC+ ·尽管两个时间序列是非平稳的,也可以用经典 的回归分析方法建立回归模型
• (d,d)阶协整是一类非常重要的协整关系, 它的经济意义在于:两个变量,虽然它们具有 各自的长期波动规律,但是如果它们是(d,d) 阶协整的,则它们之间存在着一个长期稳定的 比例关系。 • 例如,中国CPC和GDPPC,它们各自都是2阶单整,如果 它们是(2,2)阶协整,说明它们之间存在着一个长期稳 定的比例关系,从计量经济学模型的意义上讲,建立 如下居民人均消费函数模型是合理的。 CPCt =0 +1 GDPPCt + t • 尽管两个时间序列是非平稳的,也可以用经典 的回归分析方法建立回归模型