石所手大学 “回归”的历史渊源 SHIHEZI UNIVERSITY ■ 儿子们身高向着平均身高“回归”,以保持种族的稳 定 185 180 175 170 165 x 160 140 150160 170180 190 200 X 2024/9/22 石河子大学经管学院一一唐勇
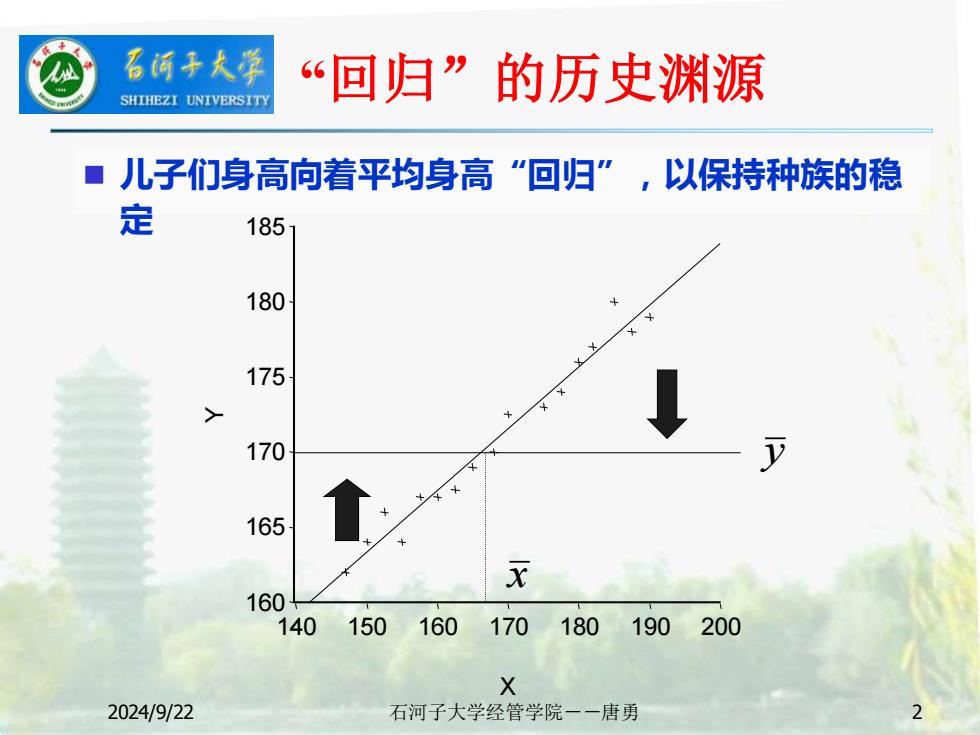
2024/9/22 石河子大学经管学院--唐勇 2 “回归”的历史渊源 ◼ 儿子们身高向着平均身高“回归”,以保持种族的稳 定 y x 160 165 170 175 180 185 140 150 160 170 180 190 200 Y X

名两子大学 回归的现代释义 SHIHEZI UNIVERSITY 回归分析是研究一个因变量对一个或多个自 变量的依赖关系,其用意在于通过后者的已 知或设定值,去估计和(或)预测前者的 (总体)均值。 >例1:给定父辈的身高,找出儿辈平均身高 的变化 >例2:给定年龄,预测平均身高 2024/9/22 石河子大学经管学院一一唐勇
2024/9/22 石河子大学经管学院--唐勇 3 回归的现代释义 ◼ 回归分析是研究一个因变量对一个或多个自 变量的依赖关系,其用意在于通过后者的已 知或设定值,去估计和(或)预测前者的 (总体)均值。 ➢ 例1:给定父辈的身高,找出儿辈平均身高 的变化 ➢ 例2:给定年龄,预测平均身高

石闭手大学 SHIHEZI UNIVERSITY 本章内容 第一节一元线性回归模型的概念 第二节, 模型参数的最小二乘估计 ■第三节最小二乘估计量的统计性质及分布 ■} 第四节一元线性回归模型的统计检验 第五节一元线性回归模型的预测 第六节案例分析 2024/9/22 石河子大学经管学院一一唐勇
2024/9/22 石河子大学经管学院--唐勇 4 本章内容 ◼ 第一节 一元线性回归模型的概念 ◼ 第二节 模型参数的最小二乘估计 ◼ 第三节 最小二乘估计量的统计性质及分布 ◼ 第四节 一元线性回归模型的统计检验 ◼ 第五节 一元线性回归模型的预测 ◼ 第六节 案例分析

第一节一元线性回归模型的概念 ■一、相关关系与回归模型 ■ 各种经济变量之间的关系,可以划分为两 类:确定的函数送系和非确定性的相关关 系 1、 确定的函数关系 ■2、非确定的相关关系 2024/9/22 石河子大学经管学院一一唐勇
2024/9/22 石河子大学经管学院--唐勇 5 第一节 一元线性回归模型的概念 ◼ 一、相关关系与回归模型 ◼ 各种经济变量之间的关系,可以划分为两 类:确定的函数关系和非确定性的相关关 系 ◼ 1、确定的函数关系 ◼ 2、非确定的相关关系

石所多大学 、 相关关系与回归模型 SHIHEZI UNIVERSITY ■3、回归模型 >~回归关系指变量间非确定性的因果关系, 如果变量X、Y具有回归关系,则Y=fX, u)称为回归模型,其中u为随机扰动项 ■4、一元线性回归模型 Y=Bo+BX+u >“一元”是指只有一个自变量X(解释变 量) >“线性” 被解释变量Y是参数的线性函数 2024/9/22 石河子大学经管学院一一唐勇
2024/9/22 石河子大学经管学院--唐勇 6 一、相关关系与回归模型 ◼ 3、回归模型 ➢ 回归关系指变量间非确定性的因果关系, 如果变量X、Y具有回归关系,则Y=f(X, u)称为回归模型,其中u为随机扰动项 ◼ 4、一元线性回归模型 Y=ß0+ ß1X+u ➢ “一元” 是指只有一个自变量X(解释变 量) ➢ “线性” 被解释变量Y是参数的线性函数