注意: 被替代的支路可以是有源 十 的,也可以是无源的(例 如只含有一个电阻)。 N >但不能含有受控源或是受 控源的控制量! 原电路 4为“N中某个受控源的控制量, 替代后u不存在了。 替代定理也称置换定理。电路分析 N 时可简化电路;有些新的等效变换 方法与定理用它导出;实践中,采 用假负载对电路进行测试,或进行 新电路 模拟试验也以此为理论依据。 16
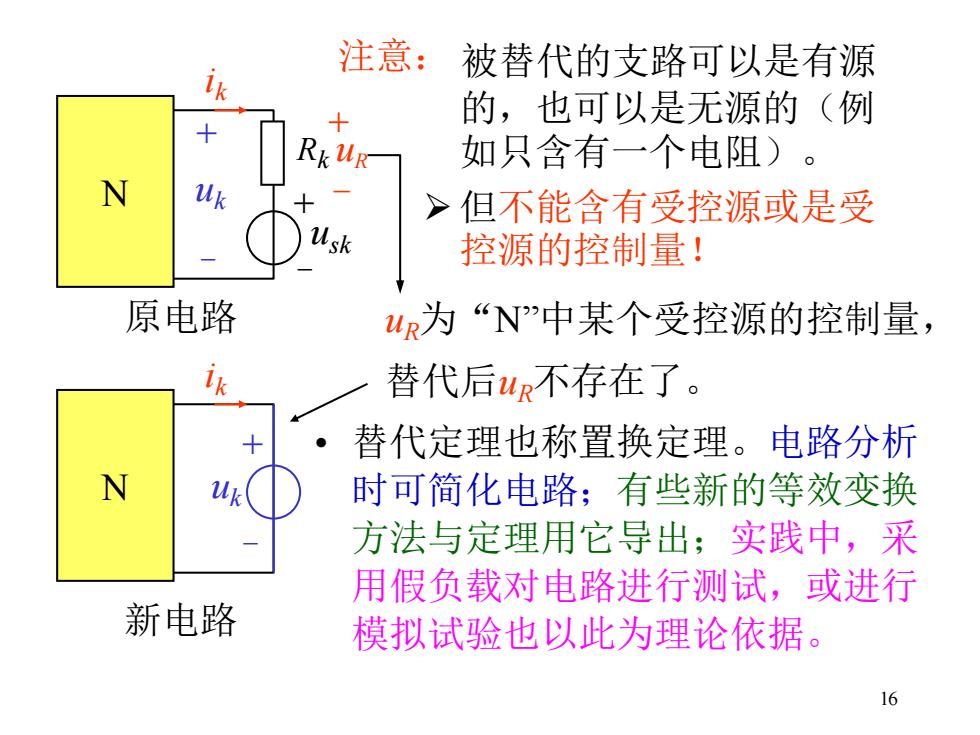
16 注意: 被替代的支路可以是有源 的,也可以是无源的(例 如只含有一个电阻)。 ➢ 但不能含有受控源或是受 控源的控制量! • 替代定理也称置换定理。电路分析 时可简化电路;有些新的等效变换 方法与定理用它导出;实践中,采 用假负载对电路进行测试,或进行 模拟试验也以此为理论依据。 + - uR usk ik N + - Rk + - uk ik N uk + - 原电路 新电路 uR为“N”中某个受控源的控制量, 替代后uR不存在了
应用举例1 己知u3=8V 求i、2、3时可 用替代定理。 =8 =1A 13 用8V 4 20-8=2A 6 电压 源替 i3=i1-i2=1A 代w3 17
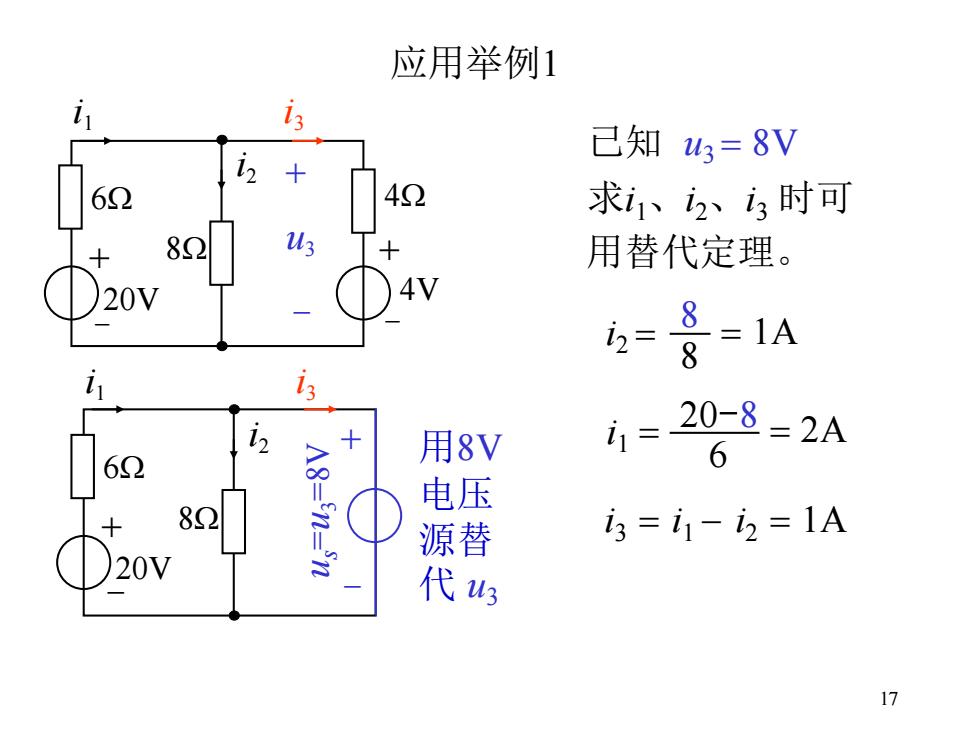
17 应用举例1 已知 u3 = 8V 求i1、i2、i3 时可 + 用替代定理。 - 20V i2 6W i1 8W + - 4V 4W i3 + - u3 + - 20V i2 6W i1 8W i3 + - u s = u 3=8V 用8V 电压 源替 代 u3 i2 = 8 8 = 1A i1 = 20-8 6 = 2A i3 = i1 - i2 = 1A
应用举例2 i ↓3 若己知i3=1A 可用替代定理求1、 8 i2、3 20V i2=i1-1=1A 6i1+8(i1-1)=20 用1A i1=2A 电流 89 源替 w3=8i2=8V 代5 18
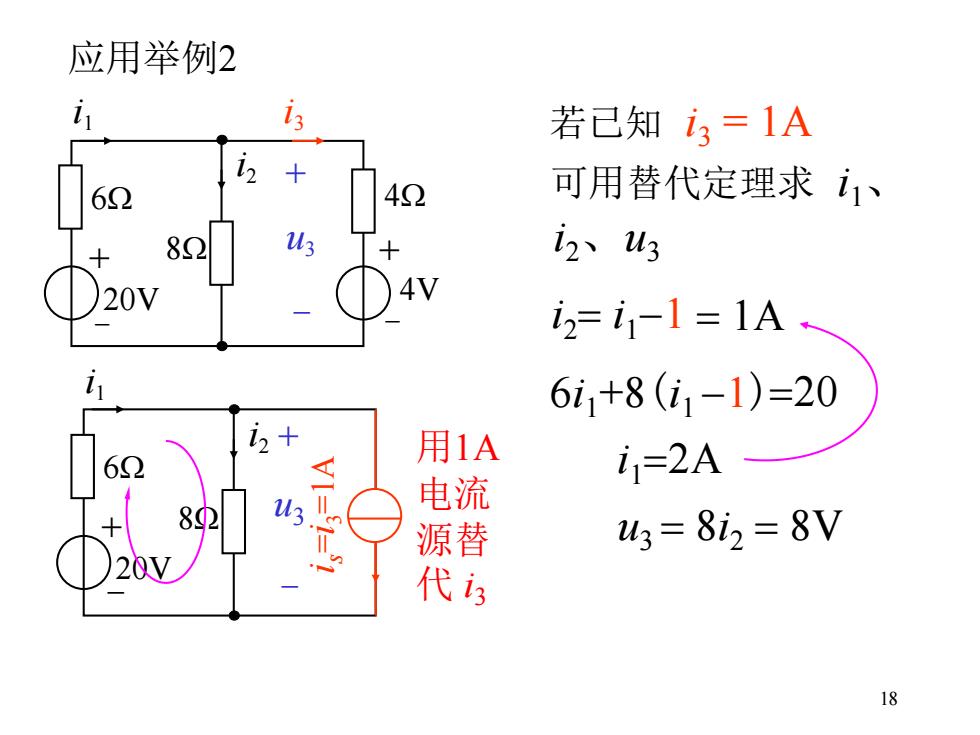
18 应用举例2 若已知 i3 = 1A 可用替代定理求 i1、 i + 2、u3 - 20V i2 6W i1 8W + - 4V 4W i3 + - u3 用1A 电流 源替 代 i3 + - 20V i2 6W i1 8W + - i s = i 3 u3 =1A i2= i1-1 6i1+8(i1 -1)=20 i1=2A = 1A u3 = 8i2 = 8V
补充例题:求1 5 22 82 22 8V 4A 22 8V 1A 4A 22 82 8 4A i= 2+8 ×(4-1)=2.4A 19
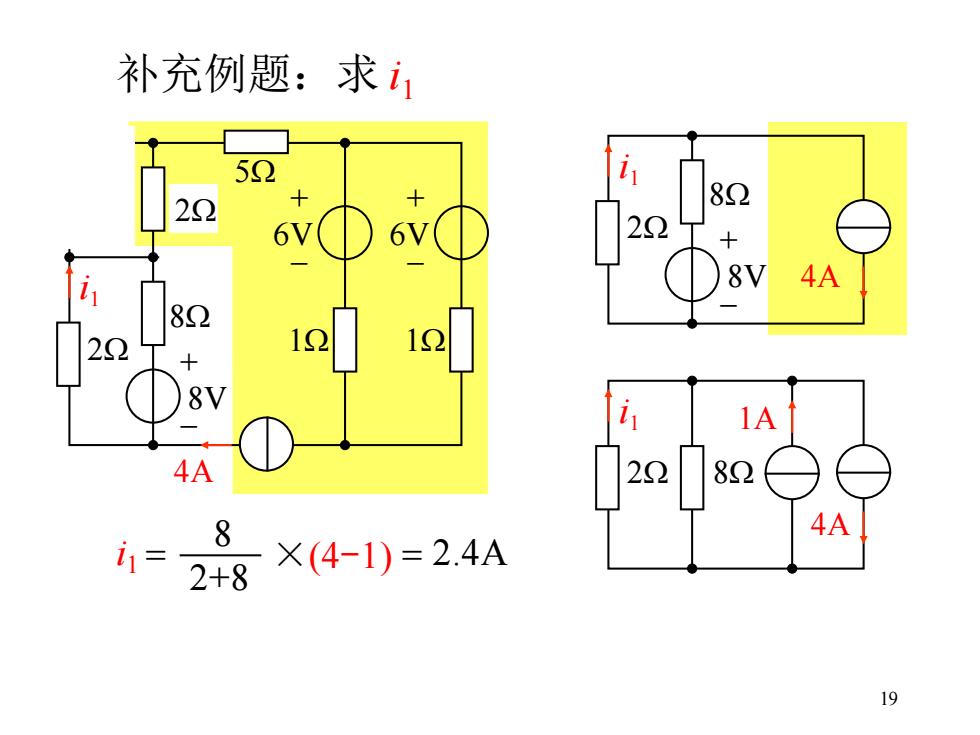
19 补充例题:求 i1 + - i1 8V 3W 6W 5W 8W 2W 4A + - 6V 1W + - 6V 1W 2W + - i1 8V 8W 2W 4A i1 2W 8W 4A 1A i1 = 2+8 8 ×(4-1) = 2.4A
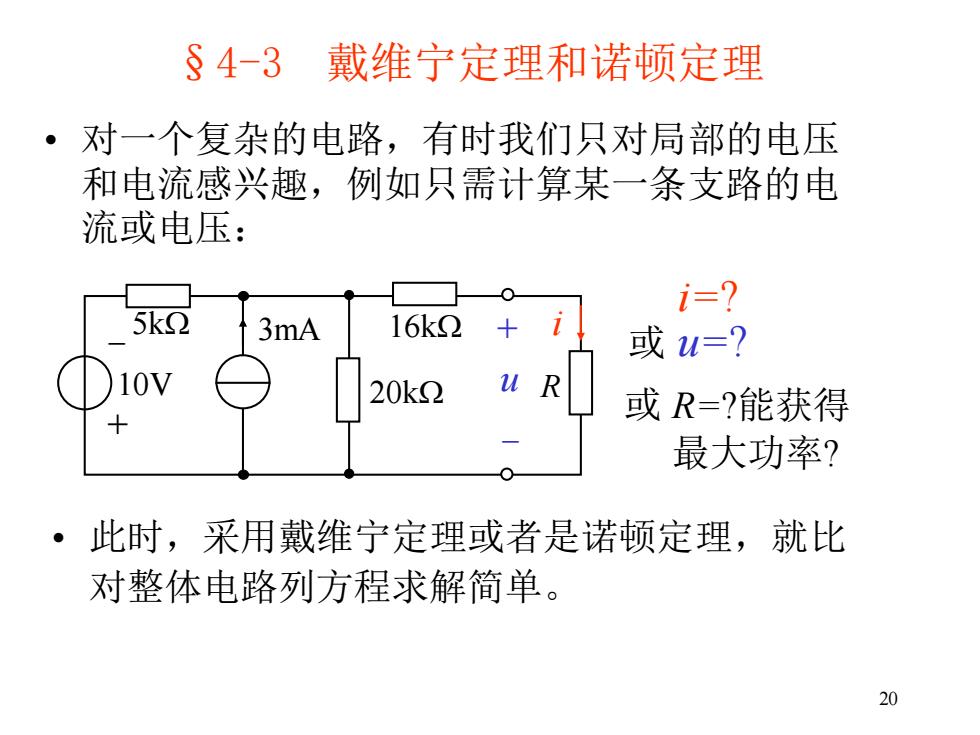
§4-3 戴维宁定理和诺顿定理 ·对一个复杂的电路,有时我们只对局部的电压 和电流感兴趣,例如只需计算某一条支路的电 流或电压: i=? 5kΩ 3mA 16k2 或u=? 10V 20k2 或R=?能获得 最大功率? ·此时,采用戴维宁定理或者是诺顿定理,就比 对整体电路列方程求解简单。 20
20 §4-3 戴维宁定理和诺顿定理 • 对一个复杂的电路,有时我们只对局部的电压 和电流感兴趣,例如只需计算某一条支路的电 流或电压: • 此时,采用戴维宁定理或者是诺顿定理,就比 对整体电路列方程求解简单。 + - 10V R 5kW 3mA i 20kW 16kW + - u i=? 或 u=? 或 R=?能获得 最大功率?