
注意:函数的单调性是一个区间上的性质,要用 导数在这一区间上的符号来判定,而不能用一 点处的导数符号来判别一个区间上的单调性. 二、单调区间求法 问题:如上例,函数在定义区间上不是单调的, 但在各个部分区间上单调 定义:若函数在其定义域的某个区间内是单调 的,则该区间称为函数的单调区间: 导数等于零的点和不可导点,可能是单调区间 的分界点. 方法:用方程f'(x)=0的根及f'(x)不存在的点 来划分函数f(x)的定义区间,然后判断区间内导 数的符号
注意:函数的单调性是一个区间上的性质,要用 导数在这一区间上的符号来判定,而不能用一 点处的导数符号来判别一个区间上的单调性. 二、单调区间求法 问题:如上例,函数在定义区间上不是单调的, 但在各个部分区间上单调. 定义:若函数在其定义域的某个区间内是单调 的,则该区间称为函数的单调区间. 导数等于零的点和不可导点,可能是单调区间 的分界点. 方法: . ( ) , ( ) 0 ( ) 数的符号 来划分函数 的定义区间 然后判断区间内导 用方程 的根及 不存在的点 f x f x = f x
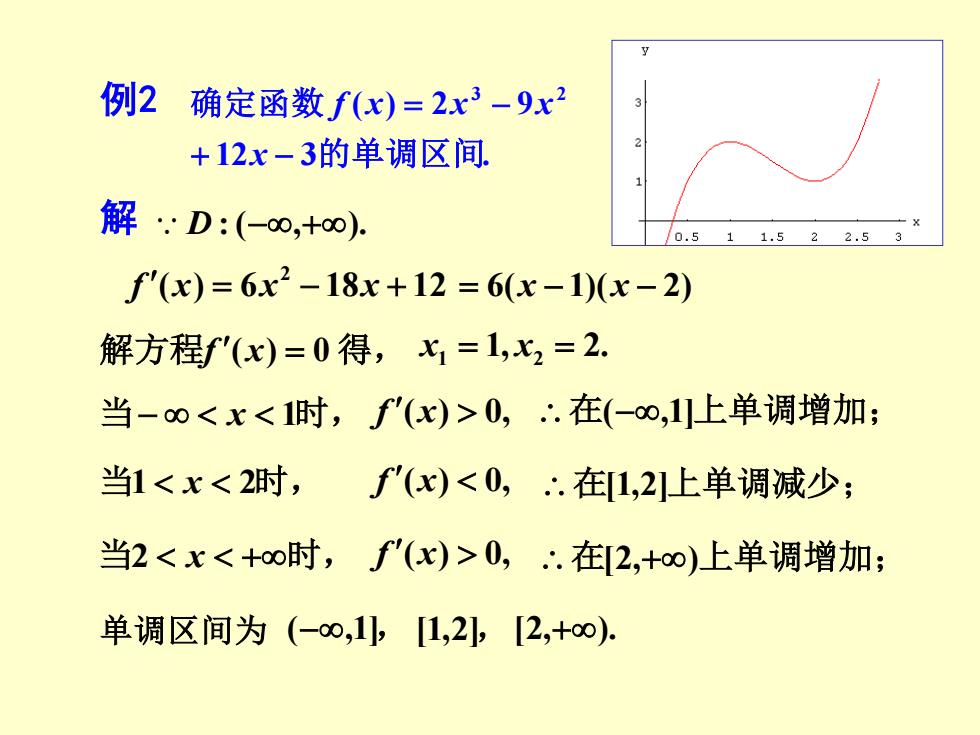
例2确定函数fx)=2x3-9x2 +12x-3的单调区间. 解D:(-o0,+o) 0.511.522.53 f'(x)=6x2-18x+12=6(x-1)(x-2) 解方程f'(x)=0得,1=1,x2=2. 当-oo<x<1时,f'(x)>0,∴.在(-oo,1上单调增加; 当1<x<2时,f'(x)<0,∴.在1,2上单调减少: 当2<x<+oo时,f'(x)>0,∴.在2,+o)上单调增加; 单调区间为(-∞,1,[1,2,[2,+∞)
例2 12 3 . ( ) 2 9 3 2 的单调区间 确定函数 + − = − x f x x x 解 D :(−,+). ( ) 6 18 12 2 f x = x − x + = 6(x − 1)(x − 2) 解方程f (x) = 0 得, 1, 2. x1 = x2 = 当− x 1时, f (x) 0, 在(−,1]上单调增加; 当1 x 2时, f (x) 0, 在[1,2]上单调减少; 当2 x +时, f (x) 0, 在[2,+)上单调增加; 单调区间为 (−,1], [1,2],[2,+)