
例 y=cosx sinx
例
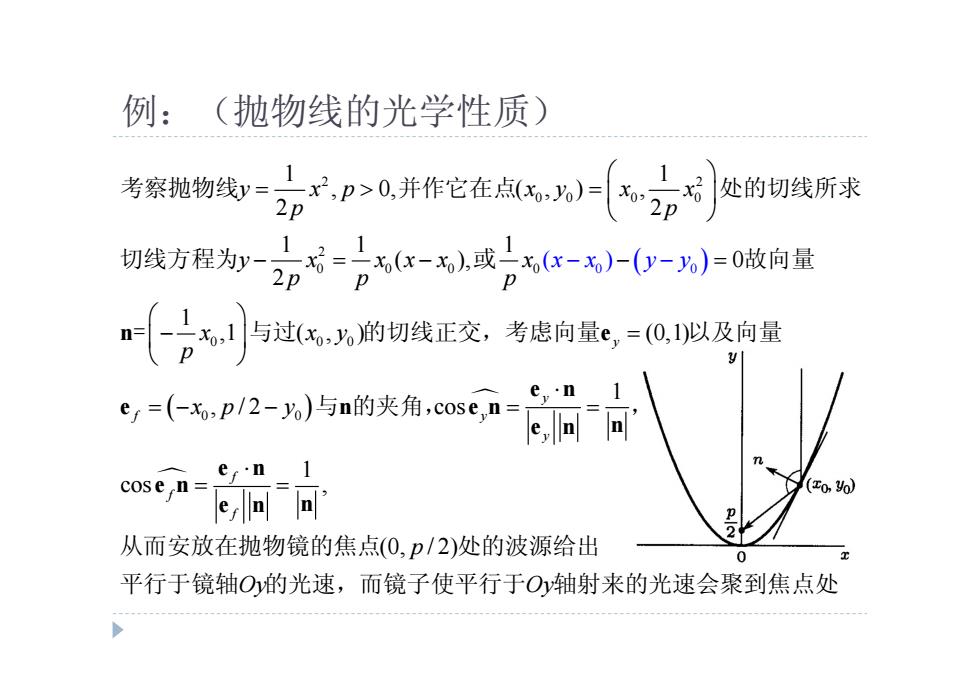
例:(抛物线的光学性质) 老察数划Dp>0并作它在点-(办 处的切线所求 2p 切发方#为郑2式--1或)0-)-0做向量 p 台 与过(x,)的切线正交,考虑向量c,=(0,1)以及向量 ey'n 1 ef=(-x,p/2-yo)与n的夹角,cose,n= cosen= (o.Yo em▣ 从而安放在抛物镜的焦点(0,p/2)处的波源给出 2 0 平行于镜轴O的光速,而镜子使平行于O轴射来的光速会聚到焦点处
2 2 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 1 1 , 0, ( , ) , 2 2 1 1 1 ( ), 0 2 1 ,1 ( , ) (0,1) 1 , / 2 cos , ( 1 cos ) y y f y y f f f y x p x y x x x x y y p p y x x x x x p p p x x y p x p y n e e n e n e n e n n e n e n e n n 考察抛物线 并作它在点 处的切线所求 切线方程为 或 故向量 = 与过 的切线正交,考虑向量 以及向量 与 的夹角, , 从而 (0, / 2) p Oy Oy 安放在抛物镜的焦点 处的波源给出 平行于镜轴 的光速,而镜子使平行于 轴射来的光速会聚到焦点处 例:(抛物线的光学性质)
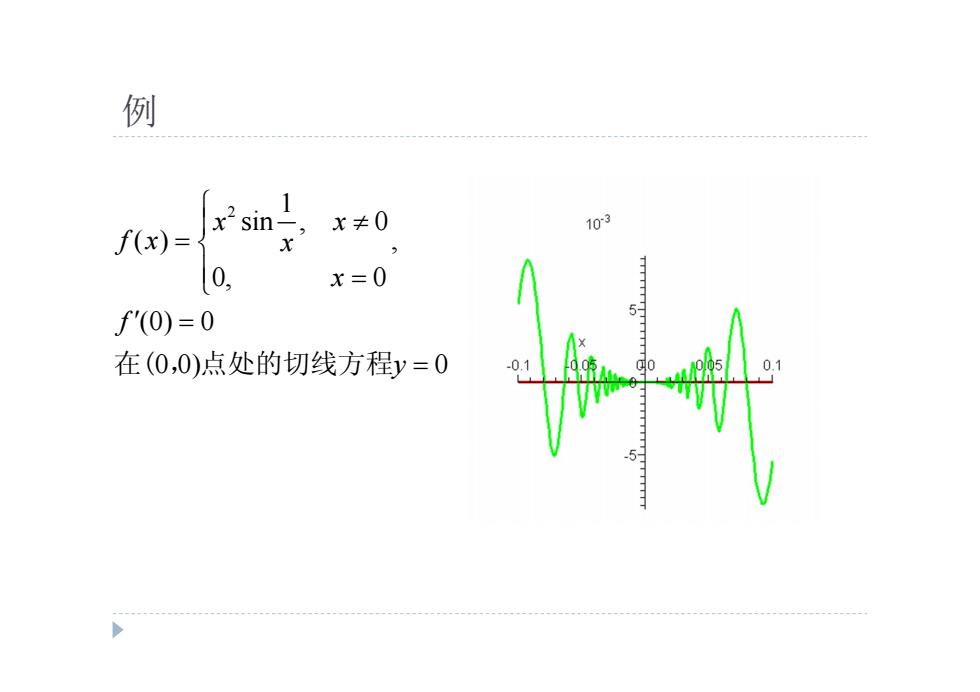
例 1 x2 sin-, x≠0 103 f(x)= 0 x=0 f'(0)=0 在(0,0)点处的切线方程y=0 .5
例 2 1 sin , 0 ( ) , 0, 0 (0) 0 0 0) 0 x x f x x x f y 在( ,点处的切线方程
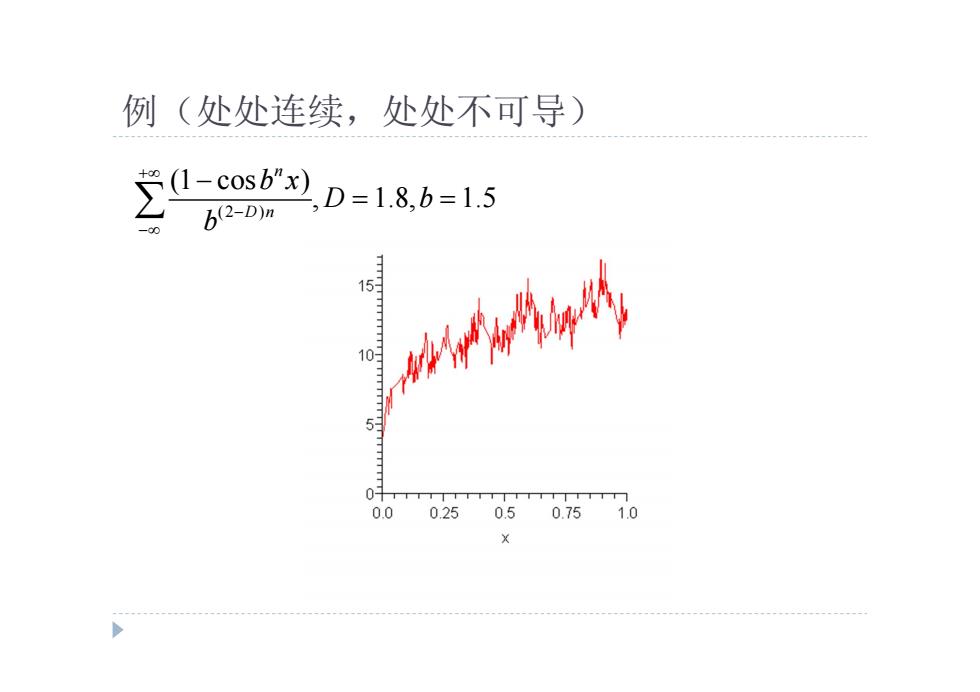
例(处处连续,处处不可导) 2,osb,D=18b-=15 b(2-D)n 15 H 103 5 0.0 0250.50.75 1.0
例(处处连续,处处不可导) (2 ) (1 cos ), 1.8, 1.5 n D n b x D b b
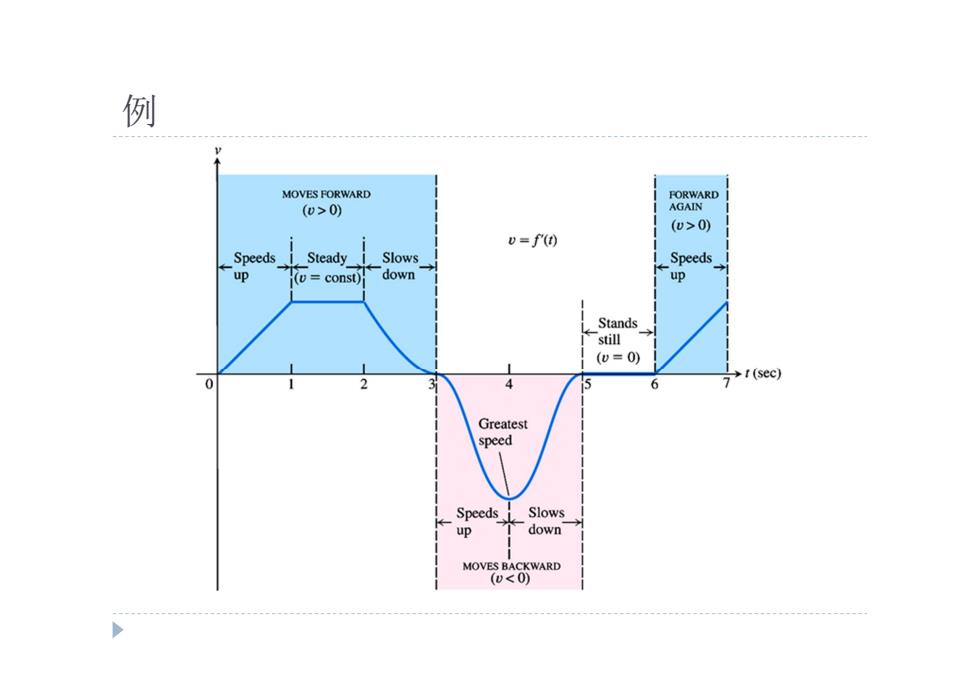
例 MOVES FORWARD FORWARD (0>0) AGAIN (0>0) v=f'() Speeds Steady Slows Speeds up (v=const) down up Stands still (0=0) t(sec) 0 6 Greatest speed Speeds Slows down MOVES BACKWARD (0<0)
例