
切线 如果函数f:E→R定义在集合EcR且在点x∈E处可导,那么方程 y-f(xo)=f(xo)(x-xo) 给出的直线就叫做这个函数图像在点(x,f(x)的切线
切线 0 0 0 0 0 0 ( )( ) : ( , ( )) y f x f f E E x E x f x x x x 如果函数 定义在集合 且在点 处可导,那么方程 给出的直线就叫做这个函数图像在点 的切线
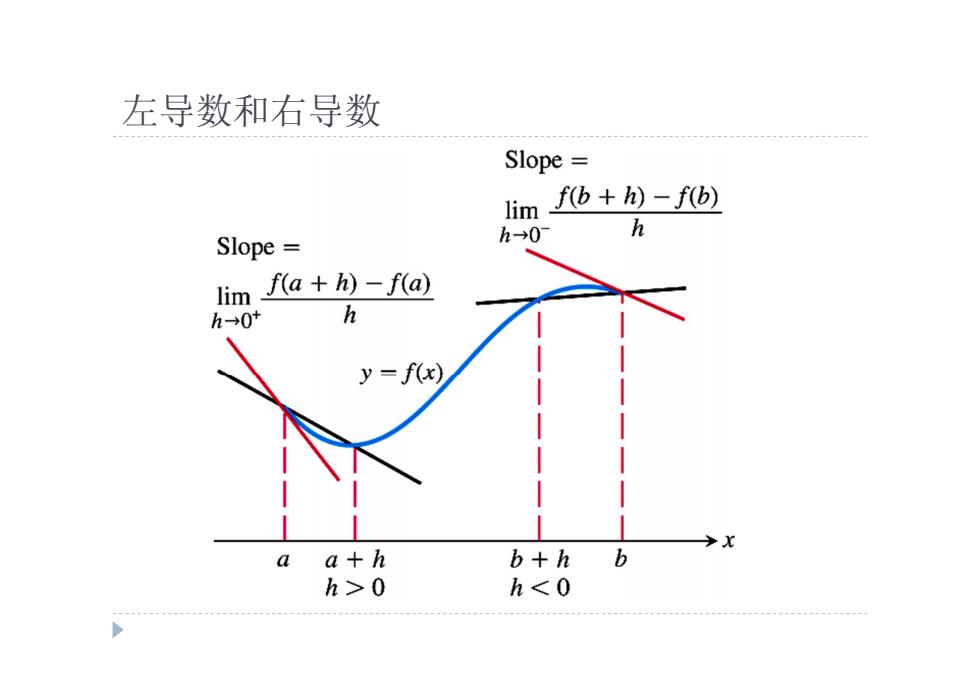
左导数和右导数 Slope= limbh)-f(b) h→0 h Slope= lim fa+h)-f(a) h→0* h y=f(x) aa+h b+h b h>0 h<0
左导数和右导数

例 (x)=ax-,a∈R,(0<x<+o) (a)=a*lna,(a>0,a≠l,x∈R) (o.)-zhg(-Oazwaz) (sinx)'=cosx,(cosx)=-sinx
例 1 , , 0 ln , 0, 1, 1 log , 0, 0, 1 ln sin cos , cos sin x x a x x x a a a a a x x x a a x a x x x x

例 1、考察f(x)=x在x=0处的可导性 .1 2、考察函数f(x)= xsin,x≠0 x=0处的连续性和可导性 0, x=0 3、设函数f:(0,+o)→R在x=1处可导,且 f(xy)=f(x)+f(y),x,y∈(0,+o) 证明f在0,+∞处处可导,并且旷(=C田+f0
例 1 ( ) 0 、考察f x x x 在 处的可导性 1 sin , 0 2 ( ) 0 0, 0 x x f x x x x 、考察函数 在 处的连续性和可导性 3 : (0, ) 1 ( ) ( ) ( ), , (0, ) ( ) (0, ) ( ) (1) f x f xy yf x xf y x y f x f f x f x 、设函数 在 处可导,且 证明 在 处处可导,并且

例 奇函数的导函数为偶函数 ,偶函数的导函数为奇函数 周期函数的导函数还是周期函数
例 奇函数的导函数为偶函数 偶函数的导函数为奇函数 周期函数的导函数还是周期函数