
人衣 第五节函数的极值与最大值最小值 一、函数的极值及其求法 二、最大值最小值问题
山东农业大学 高等数学 主讲人:苏本堂 第五节函数的极值与最大值最小值 一、函数的极值及其求法 二、最大值最小值问题
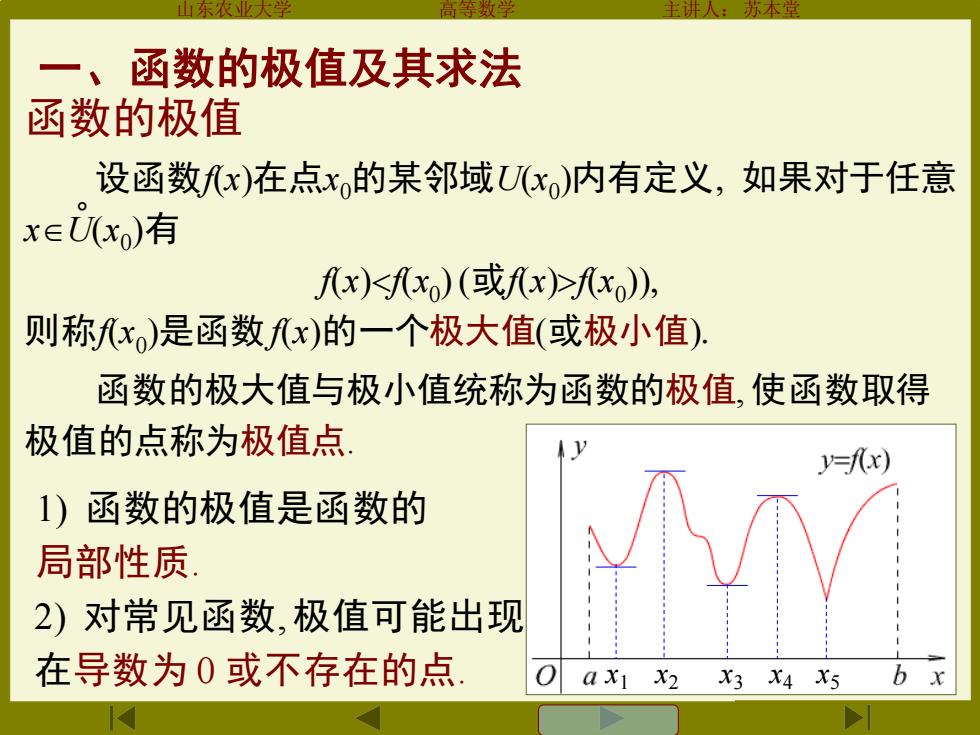
山东农业大 本雪 、函数的极值及其求法 函数的极值 设函数x)在点x的某邻域Uxo)内有定义,如果对于任意 xeU(x)有 fx)<x)(或x)>x) 则称x)是函数x)的一个极大值(或极小值), 函数的极大值与极小值统称为函数的极值,使函数取得 极值的点称为极值点, y=f(x) 1)函数的极值是函数的 局部性质 2)对常见函数,极值可能出现 在导数为0或不存在的点 aXI X2 X3 X4 X5 b
山东农业大学 高等数学 主讲人:苏本堂 函数的极值 设函数f(x)在点x0的某邻域U(x0 )内有定义 如果对于任意 xU(x0 )有 f(x)f(x0 ) (或f(x)f(x0 )) 则称f(x0 )是函数f(x)的一个极大值(或极小值) 。 x1 x2 x3 x4 x5 函数的极大值与极小值统称为函数的极值, 使函数取得 极值的点称为极值点. 一、函数的极值及其求法 2) 对常见函数, 极值可能出现 在导数为 0 或不存在的点. 1) 函数的极值是函数的 局部性质

定理1(必要条件) 设函数孔x)在点x处可导,且在x处取得极值, 那么f'(xo=0. 驻点 使导数f'(x)为零的点(方程f'(x)=O的实根)称为函数x) 的驻点 思考: 极值点是否一定是驻点?驻点是否一定是极值点? 思考: 极值点不一定是驻点.如=x,x=0是极值点,但不可导 驻点不一定是极值点.如y=x3,x=0是驻点,但不是极值点
山东农业大学 高等数学 主讲人:苏本堂 设函数f(x)在点x0处可导, 且在x0处取得极值, 那么f (x0 )=0. 驻点 使导数f (x)为零的点(方程f (x)=0的实根)称为函数f(x) 的驻点. 定理1(必要条件) 思考: 极值点是否一定是驻点? 驻点是否一定是极值点? 思考: 极值点不一定是驻点. 如y=|x|,x=0是极值点,但不可导 驻点不一定是极值点.如y=x 3 ,x=0是驻点,但不是极值点

山东农业大 定理2(极值第一判别法) 设函数f(x)在xo的某邻域内连续,且在空心邻域 内有导数,当x由小到大通过x时, (1)f'(x)“左正右负” 则f(x)在x取极大值。 (2)∫'(x)“左负右正” 则f(x)在x取极小值; 点击图中任意处动画播放暂停 确定极值点和极值的步骤 (1)求出导数f'(x): (2)求出x)的全部驻点和不可导点, (3)考察在每个驻点和不可导点的左右邻近f'(x)的符号; (4)确定出函数的所有极值点和极值
山东农业大学 高等数学 主讲人:苏本堂 定理 2 (极值第一判别法) ( ) , 设函数 f x 在x0的某邻域内连续 且在空心邻域 内有导数, , 当x由小到大通过 x0时 (1) f (x) “左正右负” , ( ) ; 则f x 在x0 取极小值 (2) f (x) “左负右正” , ( ) . 则f x 在x0 取极大值 点击图中任意处动画播放\暂停 确定极值点和极值的步骤 (1)求出导数f (x); (2)求出f(x)的全部驻点和不可导点; (3)考察在每个驻点和不可导点的左右邻近f (x)的符号; (4)确定出函数的所有极值点和极值

例1.求函数f(x)=(x-1)x3的极值 解0求导数了0+x-x- 2)求极值可疑点 令f'(x)=0,得x1=号;令f"'(x)=o,得x2=0 3)列表判别 x(-0,0) (0,) 25 (层,+0) f'(x) 0 f(x) 0 0.33 .x=0是极大点,其极大值为f(0)=0 x=号是极小点,其极小值为f()=-0.33
山东农业大学 高等数学 主讲人:苏本堂 例1. 求函数 的极值 . 解:1) 求导数 = 3 + 2 f (x) x 3 1 3 2 ( 1) − x − x 3 5 2 3 5 x x− = 2) 求极值可疑点 令 f (x) = 0 , 得 ; 5 2 x1 = 令 f (x) = , 得 x2 = 0 3) 列表判别 x f (x) f (x) 0 5 2 0 + − + 0 − 0.33 (−, 0) (0 , ) 5 2 ( , ) 5 2 + 是极大点,其极大值为 是极小点,其极小值为