
第五章习题课 一、与定积分概念有关的问题的解法 二、有关定积分计算和证明的方法
山东农业大学 高等数学 主讲人:苏本堂 二、有关定积分计算和证明的方法 一、与定积分概念有关的问题的解法 第五章习题课
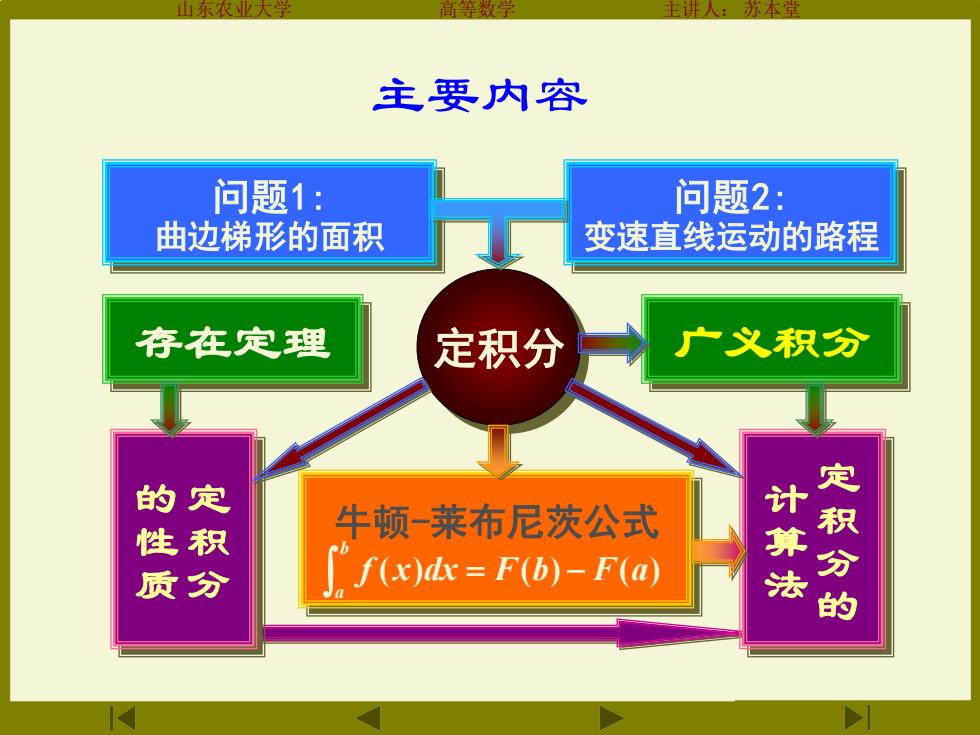
方本堂 主要内容 问题1: 问题2: 曲边梯形的面积 变速直线运动的路程 存在定理 定积分 广义积分 的定 供数 牛顿-莱布尼茨公式 f(x)dx=F(b)-F(a) 计算法 定积分的
山东农业大学 高等数学 主讲人:苏本堂 问题1: 曲边梯形的面积 问题2: 变速直线运动的路程 存在定理 定积分 广义积分 定 积 分 的 性 质 定 积 分 的 计 算 法 牛顿-莱布尼茨公式 f (x)dx F(b) F(a) b a = − 主要内容

一、与定积分概念有关的问题的解法 1.用定积分概念与性质求极限 2.用定积分性质估值 3.与变限积分有关的问题 求 dx. 解:因为xe0,时0ste 1+ex≤x”所以 n+1 利用夹逼准则得 dx=0
山东农业大学 高等数学 主讲人:苏本堂 一、与定积分概念有关的问题的解法 1. 用定积分概念与性质求极限 2. 用定积分性质估值 3. 与变限积分有关的问题 例1. 求 d . 1 lim 1 0 x e x e x n x n → + 解: 因为 时, x n x e x e + 1 0 所以 x e x e x n x d 1 1 0 + 0 x x n d 1 0 1 1 + = n 利用夹逼准则得 d 0 1 lim 1 0 = + → x e x e x n x n , n x

等数学 主讲人:苏本堂 例2.求极限 解:原式=[ 1 从上式可以看出它是西数 在[0,1]上的 一个积分和式,于是 20 6
山东农业大学 高等数学 主讲人:苏本堂 2 2 2 2 2 4 1 4 2 1 4 1 1 [ lim n n n n − n + + − + → − 例2. 求极限 ] 4 ( ) 1 4 ( ) 1 ) 2 4 ( 1 1 4 1 [ 1 2 2 2 2 n n n i n n n − + + − + + − + − 解:原式= 一个积分和式,于是 从上式可以看出它是函数 2 在[0,1]上的 4 1 ( ) x f x − = 原式 dx x − = 1 0 2 4 1 0 1 2 arcsin x = 6 =

2n 2 例3.求极限lim( 十十 n->oo n+1n+ n+1 n 1 n 1 n 解: lim >2m n->oon+1 ∑2r≤原式≤lim i= n→ni=l 左边-4三2日2”dx non+1= In 2 右边-四22-血之2-2r1x点 n→on i=1 n→0 i=1 n 2 2, 2 1 利用夹逼准则得 lim 十十 n->a0 n+1n+3 n+ In 2
山东农业大学 高等数学 主讲人:苏本堂 例3. 求极限 ). 2 2 1 2 lim ( 1 2 1 1 2 n n n n n n n n n + + + + + → + 解: 原式 n n 1 lim → = n i n i 1 2 1 lim + = → n n n = n i n i 1 2 x x 2 d 1 0 = 1 1 lim n→ n + = n i n i 1 2 左边 右边= n n 1 lim → = n i n i 1 2 → = n lim = n i n i 1 n 2 1 x x 2 d 1 0 = 利用夹逼准则得 ) 2 2 1 2 lim ( 1 2 1 1 2 n n n n n n n n n + + + + + → +