
CERN库的随机数产生子 PAW用户 Real random(1) Call Rmarin(ISEED,0,0) 注意:用于产生子的 Call Ranmar(random,1) 随机数种子还可以用 来保证后续进程的随 Root用户 机数不重复。 gRandom->SetSeedO; 粒子物理与核物理 研究中,大都采用 Float t random gRandom->Rndm(1); CERN程序库提供 的随机数产生子
CERN库的随机数产生子 PAW用户 … gRandom->SetSeed(); … Float_t random = gRandom->Rndm(1); … … Real random(1) Call Rmarin(ISEED,0,0) … Call Ranmar(random,1) … 注意: 用于产生子的 随机数种子还可以用 来保证后续进程的随 Root 用户 机数不重复。 粒子物理与核物理 研究中,大都采用 CERN程序库提供 的随机数产生子。 粒子物理与核物理 研究中,大都采用 CERN程序库提供 的随机数产生子
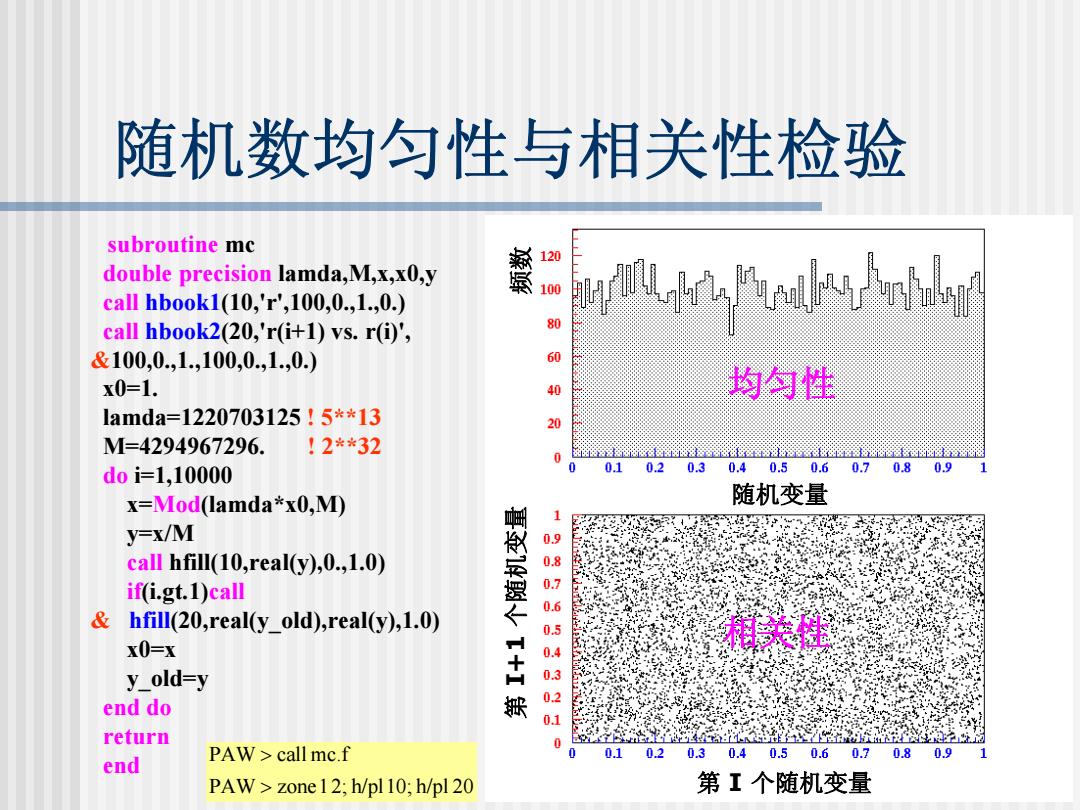
随机数均匀性与相关性检验 subroutine mc 120 double precision lamda,M,x,x0,y 100 call hbook1(10,'r',100,0.,1.,0.) call hbook2(20,'r(i+1)vs.r(i)', 80 &100,0.,1.,100,0,1.,0.) 60 x0=1. 40 均匀性 lamda=1220703125!5*13 20 M=4294967296. !2*32 doi=1,10000 0.1 0.2 0.3 0.40.50.60.7 0.80.9 x=Mod(lamda*x0,M) 随机变量 y=x/M call hfill(10,real(y),0.,1.0) if(i.gt.1)call & hfill(20,real(y_old),real(y),1.0) x0=x y_old=y N财654女 end do return 0 PAW>call mc.f 01 0.2 0.30.4 0.50.6 0.70.80.9 end PAW zone 12;h/pl 10;h/pl 20 第I个随机变量
随机数均匀性与相关性检验 subroutine mc dou ble precision lamda,M,x,x0,y call hbook 1(10,'r',100,0.,1.,0.) call hbook 2(20,'r(i+1) vs. r(i)', &100,0.,1.,100,0.,1.,0.) x0=1. lamda=1220703125 ! 5**13 M=4294967296. ! 2**32 do i=1,10000 x=Mod(lamda*x0,M) y=x/M call hfill(10,real(y),0.,1.0) if(i.gt.1)call & hfill(20,real(y_old),real(y),1.0) x0= x y_old=y end do return end 随机变量 第 I 个随机变量 第 I+1 个随机变量 频数 均匀性 相关性 PAW zone12; h/pl10; h/pl 20 PAW call mc.f > >
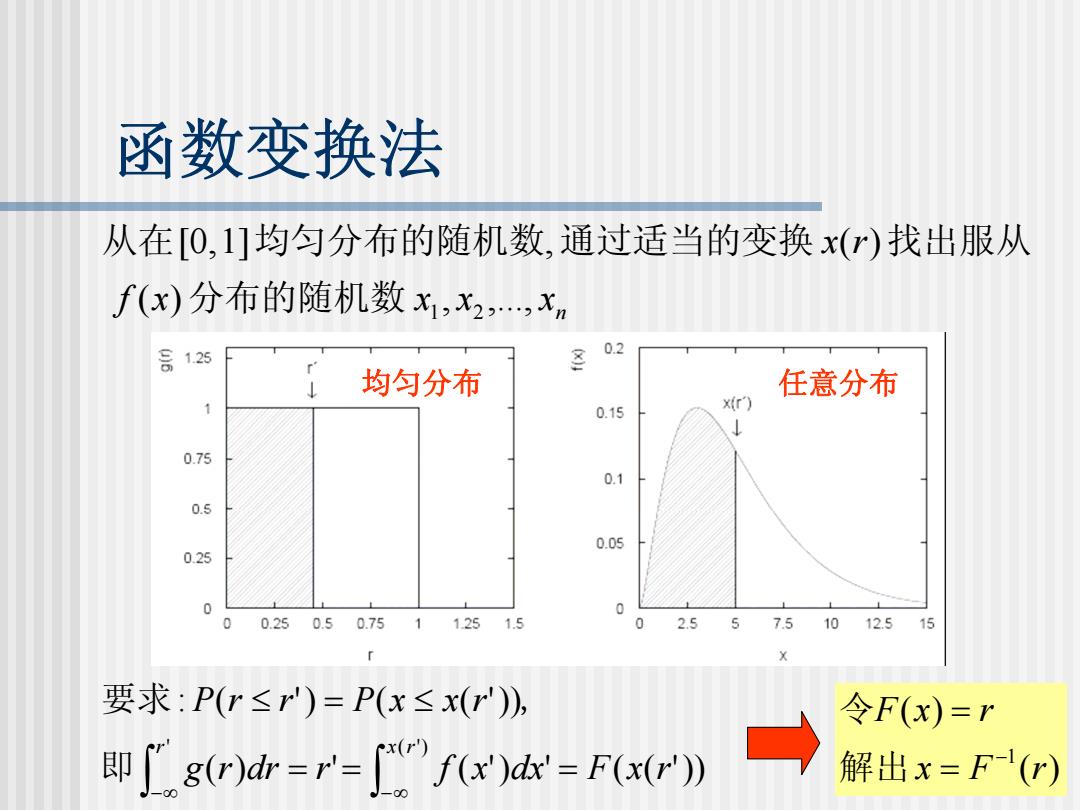
函数变换法 从在[O,1]均匀分布的随机数,通过适当的变换x(r)找出服从 f(x)分布的随机数x,x2,,xm 1.25 02 均匀分布 任意分布 1 0.15 x(r) 0.75 0.1 0.5 0.05 0.25 0 0.25 0.50.7511251.5 0 2.55 7.510 12.5 15 要求:P(r≤r)=P(x≤x(r), 令F(x)=r 即'gr)dr=r=f(x)a=F(xr》 解出x=F(r)
函数变换法 n f x x x x x r ( ) , ,..., [0,1] , ( ) 分布的随机数 1 2 从在 均匀分布的随机数 通过适当的变换 找出服从 ∫ ∫ − ∞ ∞ − = = = ≤ = ≤ ' ) ( ' ( ) ' ( ') ' ( ( ')) : ( ') ( ( ')), r r x g r dr r f x dx F x r P r r P x x r 即 要求 ( ) ( ) 1 x F r F x r − = = 解出 令 均匀分布 任意分布