复旦大学：《统计热力学》课程教学资源（课件讲稿）04 Chapter 4 经典统计和量子统计

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis innovative material Liouville(刘维)定理 由Hamilton运动方程： aH 0d= 2H Opi =q1 0qi p,oq aH =-p 中， 82H 8q, opi ap,dq, + p1=0 8qi pi 李振华制 2013/9/26 统计热力学第四章 11

李 振 华 制 2013/9/26 统计热力学第四章 11 造 Liouville（刘维）定理 由Hamilton运动方程： i i q p H     i i p q H      i i i i p q H p p        2  i i i i p q H q q       2   0      i i i i p p q q 

Center for Theoretical Chemical Physics ratory of Molecular Catalysis Innovative ma 901 Liouville(刘维)定理 所以： 09+2=0 0 oqi opi D.C ap 8t 好+ p,g i=1 台p, 上式左边正是： dp(p,q,t) dt 所以Liouville定理得证 振华制 2013/9/26 统计热力学第四章 12

李 振 华 制 2013/9/26 统计热力学第四章 12 造 Liouville（刘维）定理 所以： 上式左边正是： 0 , 1 1                    fN i i i fN i i p q i p p q t q       0      i i i i p p q q  dt d( p, q,t) 0 , 1                                            fN i i i i i i i i i p q p p q q p p q q t         所以Liouville定理得证

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material Liouville定理的推论 相体积不变原理：当考虑Γ空间中任一区域，当 这个区域的边界按照正则方程所给定的轨道运 动时，区域内的体积在运动中不变。(（证明很 简单，因为对于保守力学体系，相点总数在运 动中也保持不变) 参见：高执棣《统计热力学导论》P47. 李 华 2013/9/26 统计热力学第四章 13 造

李 振 华 制 2013/9/26 统计热力学第四章 13 造 Liouville定理的推论  相体积不变原理：当考虑Γ空间中任一区域，当 这个区域的边界按照正则方程所给定的轨道运 动时，区域内的体积在运动中不变。（证明很 简单，因为对于保守力学体系，相点总数在运 动中也保持不变） 参见：高执棣《统计热力学导论》P47

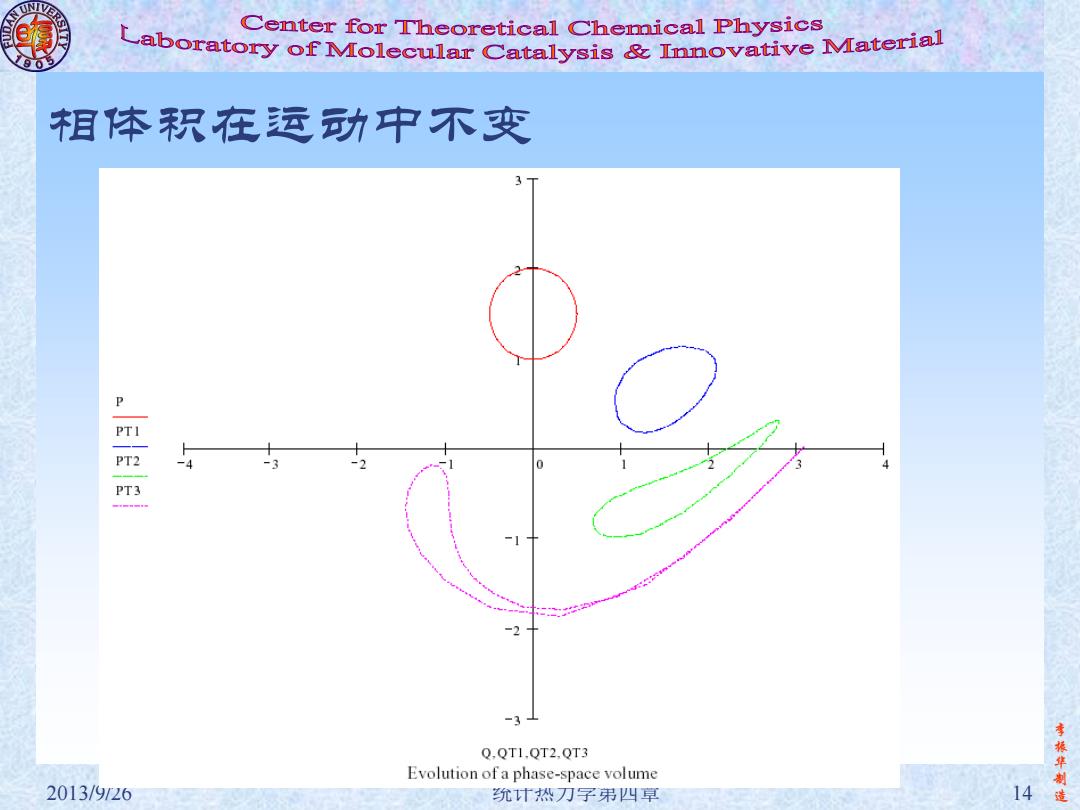
e Center for Theoretical Chemical Physics ratory of Molecular Catalysis Innovative Ma 相体积在运功中不变 3 -3 0 -3 Q.QTI.QT2.QT3 Evolution of a phase-space volume 李振华 2013/9/26 狁计热刀子弟四草 14 造

李 振 华 制 2013/9/26 统计热力学第四章 14 造 相体积在运动中不变

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material Liouville定理的推论 相空间体积元在正则变换中不变（很容易想象得 到) 若处于平衡条件下（宏观上体系的一切宏观性质 均不随时间而改变，微观上的对应则是在相空间 的任一点，相密度不随时间而改变)，在相空间 的各处，相密度皆相等。用数学语言表述就是 (即p不显含)： D,9 Liouville定理与统计热力学的基本假定有非常密切的关系。 2013/9/26 统计热力学第四章 15 造

李 振 华 制 2013/9/26 统计热力学第四章 15 造 Liouville定理的推论  相空间体积元在正则变换中不变（很容易想象得 到）。  若处于平衡条件下（宏观上体系的一切宏观性质 均不随时间而改变，微观上的对应则是在相空间 的任一点，相密度不随时间而改变），在相空间 的各处，相密度皆相等。用数学语言表述就是 （即不显含t）： Liouville定理与统计热力学的基本假定有非常密切的关系。 0 ,          p q t 