
第四章综合实验实验十四空气中声速测量频率介于20Hz~20KHz的机械波振动在弹性介质中的传播就形成声波,介于20KHz~500MHz的称为超声波,超声波的传播速度就是声波的传播速度,而超声波具有波长短、易于定向发射和汇聚等优点,声速实验所采用的声波频率一般都在20KHz~60KHz之间。在此频率范围内,采用压电陶瓷换能器作为声波的发射器和接收器效果最佳。【实验目的】1.了解超声波的产生、发射和接收的方法。2.通过实验了解压电陶瓷传感器的功能。3.进一步掌握示波器和信号发生器的使用。4.用共振干涉法、相位比较法测量声速,并加深对有关共振、振动合成、波的干涉等理论知识的理解。【实验仪器】SV-DH系列声速测试仪、示波器、声速测试仪信号源示波器声速测定仪信号发生器图4-14-1声速测定用实验仪器SV-DH系列声速测试仪的主要结构为超声波换能器(发射换能器、接收换能
第四章 综合实验 实验十四 空气中声速测量 频率介于 20Hz~20KHz 的机械波振动在弹性介质中的传播就形成声波,介于 20 KHz~500MHz 的称为超声波,超声波的传播速度就是声波的传播速度,而超 声波具有波长短、易于定向发射和汇聚等优点,声速实验所采用的声波频率一般 都在 20 KHz~60 KHz 之间。在此频率范围内,采用压电陶瓷换能器作为声波的 发射器和接收器效果最佳。 【实验目的】 1. 了解超声波的产生、发射和接收的方法。 2. 通过实验了解压电陶瓷传感器的功能。 3. 进一步掌握示波器和信号发生器的使用。 4. 用共振干涉法、相位比较法测量声速,并加深对有关共振、振动合成、波 的干涉等理论知识的理解。 【实验仪器】 SV-DH 系列声速测试仪、示波器、声速测试仪信号源 图 4-14-1 声速测定用实验仪器 SV-DH 系列声速测试仪的主要结构为超声波换能器(发射换能器、接收换能
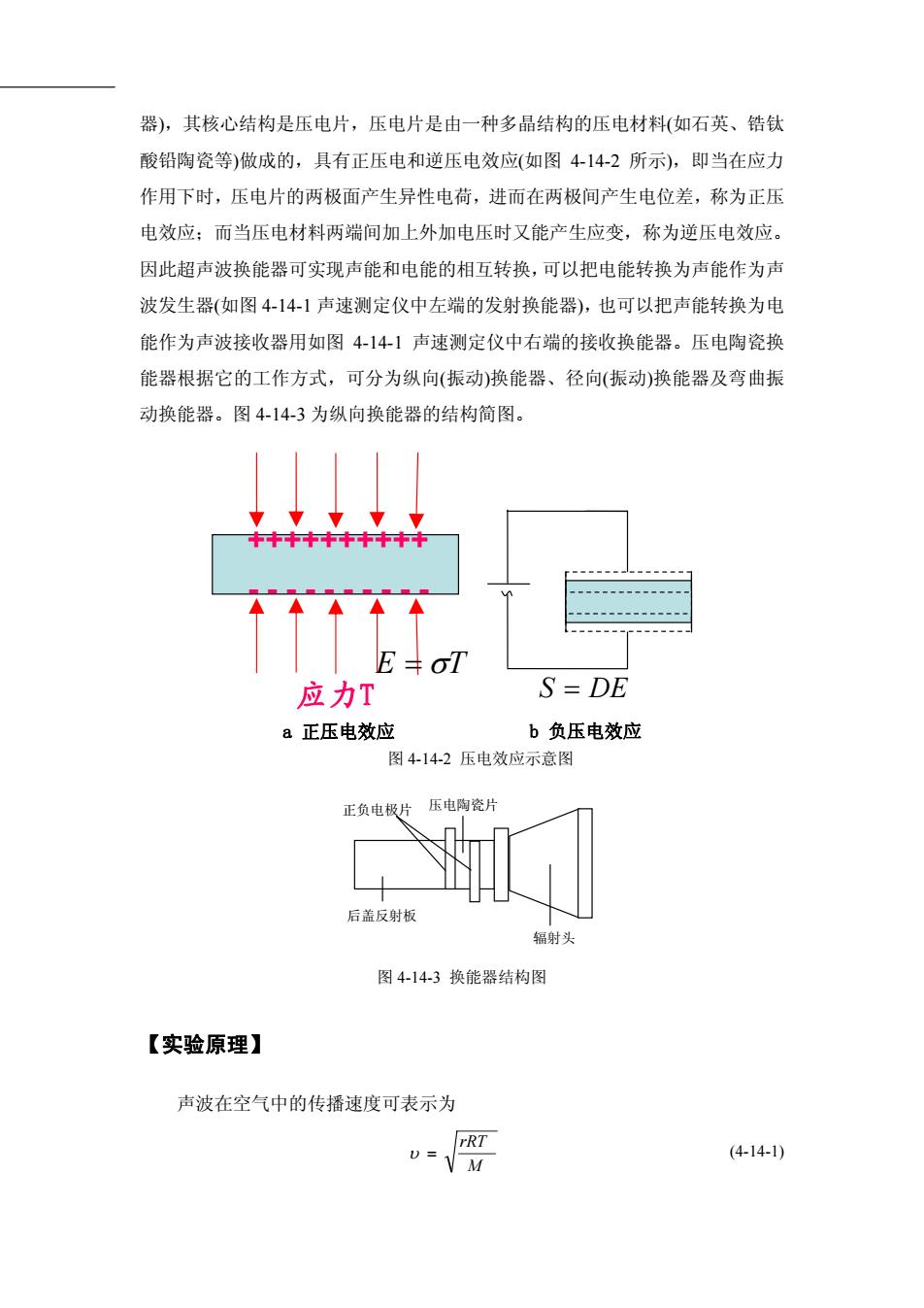
器),其核心结构是压电片,压电片是由一种多晶结构的压电材料(如石英、锆钛酸铅陶瓷等)做成的,具有正压电和逆压电效应(如图4-14-2所示),即当在应力作用下时,压电片的两极面产生异性电荷,进而在两极间产生电位差,称为正压电效应:而当压电材料两端间加上外加电压时又能产生应变,称为逆压电效应。因此超声波换能器可实现声能和电能的相互转换,可以把电能转换为声能作为声波发生器(如图4-14-1声速测定仪中左端的发射换能器),也可以把声能转换为电能作为声波接收器用如图4-14-1声速测定仪中右端的接收换能器。压电陶瓷换能器根据它的工作方式,可分为纵向(振动)换能器、径向(振动)换能器及弯曲振动换能器。图4-14-3为纵向换能器的结构简图。EoTS= DE应力Ta正压电效应b负压电效应图4-14-2压电效应示意图压电陶瓷片正负电极片后盖反射板辐射头图4-14-3换能器结构图【实验原理】声波在空气中的传播速度可表示为rRT(4-14-1)M
器),其核心结构是压电片,压电片是由一种多晶结构的压电材料(如石英、锆钛 酸铅陶瓷等)做成的,具有正压电和逆压电效应(如图 4-14-2 所示),即当在应力 作用下时,压电片的两极面产生异性电荷,进而在两极间产生电位差,称为正压 电效应;而当压电材料两端间加上外加电压时又能产生应变,称为逆压电效应。 因此超声波换能器可实现声能和电能的相互转换,可以把电能转换为声能作为声 波发生器(如图 4-14-1 声速测定仪中左端的发射换能器),也可以把声能转换为电 能作为声波接收器用如图 4-14-1 声速测定仪中右端的接收换能器。压电陶瓷换 能器根据它的工作方式,可分为纵向(振动)换能器、径向(振动)换能器及弯曲振 动换能器。图 4-14-3 为纵向换能器的结构简图。 应力T a 正压电效应 ++++++++++ - - - - - - - - - - = σTE = DES b 负压电效应 图 4-14-2 压电效应示意图 辐射头 正负电极片 压电陶瓷片 后盖反射板 图 4-14-3 换能器结构图 【实验原理】 声波在空气中的传播速度可表示为 M rRT υ = (4-14-1)

式式4-14-1中r是空气定压比热容和定容比热容之比(r=C,/C),R是普适气体常数,M是气体的摩尔质量,T是热力学温度。从式4-14-1式可以看出,温度是影响空气中声速的主要因素。如果忽略空气中水蒸汽和其他杂质的影响,在0rRT.=331.45Do=M℃(T。=273.15)时的声速m/st℃时的声速可表示为tD, = Vo /1+ 273.15(4-14-2)由波动理论知道,波的频率f、波速D和波长入之间有以下关系D= fa(4-14-3)所以只要知道频率和波长就可以求出波速。本实验用信号发生器控制换能器,故信号发生器的输出频率就是声波的频率。而声波的波长可以用共振干涉法(驻波法)、行波法(相位比较法)来进行测量。1.共振干涉法(驻波法)测量波长实验装置接线如图4-14-4所示,图中S1和S2为压电陶瓷超声换能器。S1作为超声源(如图4-14-1b中的发射换能器),信号发生器输出的正弦交变电压信号接到换能器S1上,使S1发出一平面波,且沿X方向传播。S2作为超声波接收器(如图4-14-1b中的接收换能器),把接收到的声压转换成交变的正弦电压信号后输入示波器观察,同时S2还反射一部分超声波,这样,入射波和反射波叠加,因两列波具有相同的振幅A、相同的频率f和波长入,在X轴方向上以相反的方向传播,它们的波动方程分别为y=Acos2元(ft-(4-14-4)A2 = Acos[2元(f+)+ 元](4-14-5)元入射波与反射波叠加后的方程以及声压方程为y=+2=(2Asin2元)sin2f(4-14-6)元2元P= p(ux -ux)= py (μ_二) 4fpvAcos2xsin2元ft(4-14-7)dt两波合成后,介质中各点都在作同频率的简谐振动,各点的振幅为
式式 4-14-1 中 r 是空气定压比热容和定容比热容之比( = CCr Vp ),R 是普适气 体常数,M 是气体的摩尔质量,T 是热力学温度。从式 4-14-1 式可以看出,温度 是影响空气中声速的主要因素。如果忽略空气中水蒸汽和其他杂质的影响,在 0 ℃( )时的声速 T0 = 15.273 45.331 0 0 == M rRT υ m/s t℃时的声速可表示为 15.273 1 0 t t υυ += (4-14-2) 由波动理论知道,波的频率 、波速 f υ 和波长λ 之间有以下关系 υ = fλ (4-14-3) 所以只要知道频率和波长就可以求出波速。本实验用信号发生器控制换能 器,故信号发生器的输出频率就是声波的频率。而声波的波长可以用共振干涉法 (驻波法)、行波法(相位比较法)来进行测量。 1. 共振干涉法(驻波法)测量波长 实验装置接线如图 4-14-4 所示,图中 S1 和 S2 为压电陶瓷超声换能器。S1 作为超声源(如图 4-14-1b 中的发射换能器),信号发生器输出的正弦交变电压信 号接到换能器 S1 上,使 S1 发出一平面波,且沿 X 方向传播。S2 作为超声波接 收器(如图 4-14-1b 中的接收换能器),把接收到的声压转换成交变的正弦电压信 号后输入示波器观察,同时 S2 还反射一部分超声波,这样,入射波和反射波叠 加,因两列波具有相同的振幅 A、相同的频率 和波长 f λ ,在 X 轴方向上以相反 的方向传播,它们的波动方程分别为: )(2cos 1 λ π x = ftAy − (4-14-4) ])(2cos[ 2 π λ = π ++ x ftAy (4-14-5) 入射波与反射波叠加后的方程以及声压方程为 ft x Ayyy π λ π 2sin)2sin2( 21 =+= (4-14-6) ftxvAf dt yyd vuuvp π λ π ρ ρ ρπ 2sin 2 cos4 )( )( 21 = − 入 反 =−= (4-14-7) 两波合成后,介质中各点都在作同频率的简谐振动,各点的振幅为
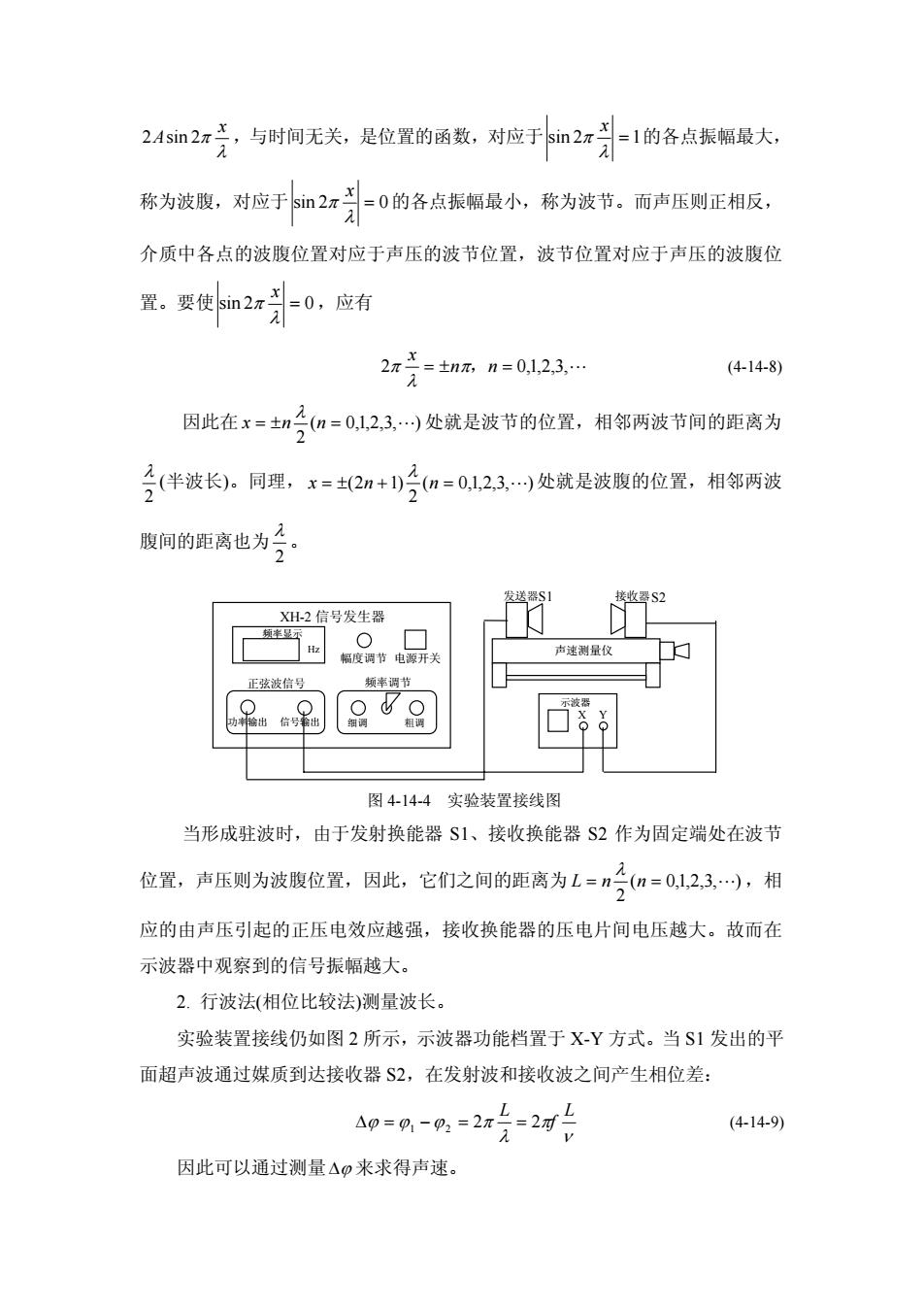
L与时间无关,是位置的函数,对应于sin2元2Asin2元=1的各点振幅最大,元元X称为波腹,对应于sin2元=0的各点振幅最小,称为波节。而声压则正相反,A介质中各点的波腹位置对应于声压的波节位置,波节位置对应于声压的波腹位x置。要使sin2元=0,应有a2=±n元,n=0,1,2,3,.(4-14-8)17因此在x=(n=0,1,2,3)处就是波节的位置,相邻两波节间的距离为+n2(半波长)。同理,x=±(2n+1)(n=0,1,2,3,.)处就是波腹的位置,相邻两波2腹间的距离也为二2发送器S1接收器S2XH-2信号发生器频率显示广0声速测量仪幅度调节电源开关频率调节正弦波信号?CCO信号编细调相调图4-14-4实验装置接线图当形成驻波时,由于发射换能器S1、接收换能器S2作为固定端处在波节4位置,声压则为波腹位置,因此,它们之间的距离为L=n(n=0,1,2,3,..),相2应的由声压引起的正压电效应越强,接收换能器的压电片间电压越大。故而在示波器中观察到的信号振幅越大。2.行波法(相位比较法)测量波长。实验装置接线仍如图2所示,示波器功能档置于X-Y方式。当S1发出的平面超声波通过媒质到达接收器S2,在发射波和接收波之间产生相位差:L1=2f-(4-14-9)0=-2=2元-1V因此可以通过测量?来求得声速
λ π x A 2sin2 ,与时间无关,是位置的函数,对应于 = 12sin λ π x 的各点振幅最大, 称为波腹,对应于 = 02sin λ π x 的各点振幅最小,称为波节。而声压则正相反, 介质中各点的波腹位置对应于声压的波节位置,波节位置对应于声压的波腹位 置。要使 = 02sin λ π x ,应有 2 nn =±= ,3,2,1,0 L x π, λ π (4-14-8) 因此在 ),3,2,1,0( 2 nnx =±= L λ 处就是波节的位置,相邻两波节间的距离为 2 λ (半波长)。同理, ),3,2,1,0( 2 )12( nnx =+±= L λ 处就是波腹的位置,相邻两波 腹间的距离也为 2 λ 。 图 4-14-4 实验装置接线图 当形成驻波时,由于发射换能器 S1、接收换能器 S2 作为固定端处在波节 位置,声压则为波腹位置,因此,它们之间的距离为 ),3,2,1,0( 2 nnL == L λ ,相 应的由声压引起的正压电效应越强,接收换能器的压电片间电压越大。故而在 示波器中观察到的信号振幅越大。 2. 行波法(相位比较法)测量波长。 实验装置接线仍如图 2 所示,示波器功能档置于 X-Y 方式。当 S1 发出的平 面超声波通过媒质到达接收器 S2,在发射波和接收波之间产生相位差: ν π λ πϕϕϕ L f L 21 ==−=Δ 22 (4-14-9) 因此可以通过测量Δϕ 来求得声速。 XH-2 信号发生器 幅度调节 电源开关 频率调节 频率显示 功率输出 信号输出 细调 粗调 Hz X Y 正弦波信号 示波器 声速测量仪 发送器S1 接收器S2

Aβ的测定可用相互垂直振动合成的李萨如图形来进行,设输入X轴的入射波振动方程为:x = A, cos(wt+p)(4-14-10)输入Y轴的是由S2接收到的波动,其振动方程为:y= A, cos(wt+@2)(4-14-11)上两式中A和A2分别为X、Y方向振动的振幅,W为角频率,9和β,分别为X、Y方向振动的初位相,则合成振动方程为:+cos(02-01)=sin (02-0)(4-14-12)AAAA,此方程轨迹为椭圆,椭圆长、短轴和方位由相位差△=2-,来决定。当Ag=0时,由式4-14-12得y=4x,即轨迹为处于第一和第三象限的一条直线,A显然直线的斜率为,如图4-14-5(=0)所示;当A=元时,得y=-x,则AA,轨迹为处于第二和第四象限的一条直线,如图4-14-5(Φ=元)所示。改变S:和S2之间的距离L,相当于改变了发射波和接收波之间的相位差,示波器显示屏上的图形也随L不断变化。显然,当S1和S2之间距离改变半个波长△L=入/2,则△改变了元,随之振动的位相差经历了从0~元的变化,李萨如图形从斜率为正的直线变为椭圆,再变到斜率为负的直线。因此,每重复出现斜率符号相反的直线,就意味着移动半个波长,进而测得波长入和频率f,根据=f可计算出室温下声波在媒质中传播的速度。ONAHβ=00=元/29=3元/20=2元0=元图4-14-5李萨如图形与两垂直简谐运动的相位差
Δϕ 的测定可用相互垂直振动合成的李萨如图形来进行,设输入 X 轴的入射 波振动方程为: )cos( = 1 wtAx +ϕ1 (4-14-10) 输入 Y 轴的是由 S2 接收到的波动,其振动方程为: )cos( = 2 wtAy +ϕ 2 (4-14-11) 上两式中A1和A2分别为X、Y方向振动的振幅,w为角频率,ϕ1和ϕ2 分别为 X、Y方向振动的初位相,则合成振动方程为: )(sin)cos( 2 12 2 12 21 2 2 2 2 1 2 −+ −=− ϕϕϕϕ AA xy A y A x (4-14-12) 此方程轨迹为椭圆,椭圆长、短轴和方位由相位差Δϕ = ϕ −ϕ12 来决定。当 Δϕ =0 时,由式 4-14-12 得 x A A y 1 2 = ,即轨迹为处于第一和第三象限的一条直线, 显然直线的斜率为 1 2 A A ,如图 4-14-5(ϕ =0)所示;当Δϕ = π 时,得 x A A y 1 2 −= ,则 轨迹为处于第二和第四象限的一条直线,如图 4-14-5(ϕ =π )所示。 改变S1和S2之间的距离L,相当于改变了发射波和接收波之间的相位差,示 波器显示屏上的图形也随L不断变化。显然,当S1 和S2 之间距离改变半个波长 L =Δ λ 2 ,则Δϕ 改变了π ,随之振动的位相差经历了从 0~π 的变化,李萨如图 形从斜率为正的直线变为椭圆,再变到斜率为负的直线。因此,每重复出现斜率 符号相反的直线,就意味着移动半个波长,进而测得波长λ 和频率f,根据υ = λf 可计算出室温下声波在媒质中传播的速度。 ϕ = 0 ϕ = π 2/ ϕ = π ϕ = π 2/3 ϕ = 2π 图 4-14-5 李萨如图形与两垂直简谐运动的相位差