
二 收敛级数的基本性质 第八章无穷级数 性质2若级数4,分别收敛于和1,即=立,=4 7三 则级数∑(,±)也收敛,其和为s±1,即有 =1
第八章 无穷级数 性质 2 若级数 1 n n u = , 1 n n v = 分别收敛于s 和t ,即 1 1 , , n n n n u s v t = = = = 则级数 ( ) 1 n n n u v = 也收敛,其和为s t ,即有 ( ) 1 1 1 . n n n n n n n u v u v = = = = + 二、收敛级数的基本性质
二、 收敛级数的基本性质 第八章无穷级数 3 的和. (n+l1) 1 2 解根据等比级数的结论,知 =1. 1- 而由例3知乃1 2 白n(n+)) =1,所以 3 =4.1 台nn+l)
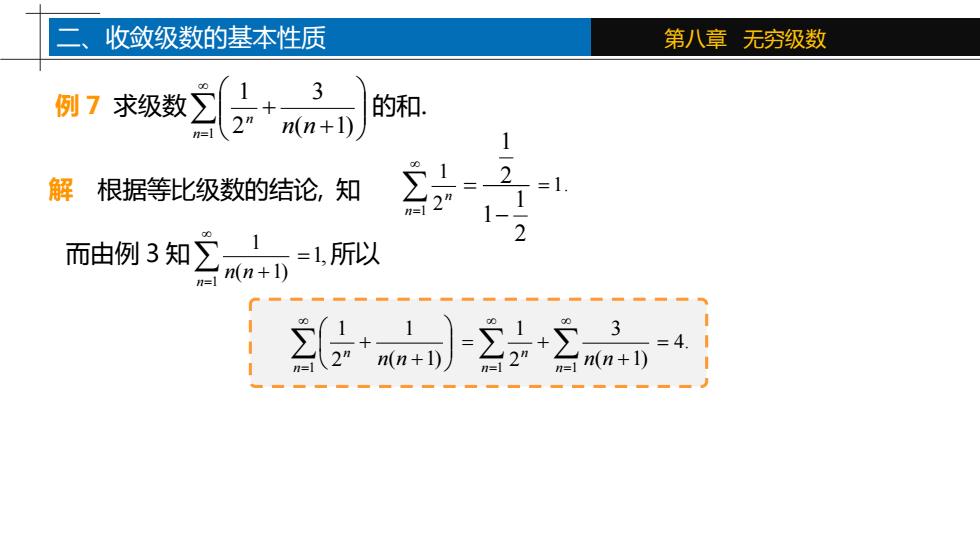
第八章 无穷级数 例 7 求级数 = + + 1 ( 1) 3 2 1 n n n n 的和. 解 根据等比级数的结论, 知 =1 2 1 n n 1 2 1 1 2 = − = 1. 而由例 3 知 = + 1 ( 1) 1 n n n =1, 所以 = + + 1 ( 1) 1 2 1 n n n n = = + = + 1 1 ( 1) 3 2 1 n n n n n = 4. 二、收敛级数的基本性质

收敛级数的基本性质 第八章无穷级数 从性质1和2可直接得出如下推论: (1)若k≠0,则级数∑a与∑k知,具有相同的收敛性; (2)若级数∑a,∑b,一个收敛-个发散,则级数∑(a,±b,)一定发散
第八章 无穷级数 从性质 1 和 2 可直接得出如下推论: (1)若k 0,则级数 1 n n a = 与 1 n n ka = 具有相同的收敛性; (2)若级数 1 n n a = , 1 n n b = 一个收敛一个发散,则级数 ( ) 1 n n n a b = 一定发散. 二、收敛级数的基本性质

收敛级数的基本性质 第八章无穷级数 例8讨论级数 的收敛性 解 因级数1发散,故2发散,又级数收敛, n=1 n n=1 2 故级数品司)行)发散
第八章 无穷级数 例 8 讨论级数 1 2 1 2 n n n = − 的收敛性. 解 因级数 1 1 n n = 发散, 二、收敛级数的基本性质 故 1 2 n n = 发散, 故级数 1 2 1 2 n n n = − 1 1 1 2 n n n = − 发散. 又级数 1 1 2 n n = 收敛

二 收敛级数的基本性质 第八章无穷级数 性质3(级数收敛的必要条件) 如果级数∑4,收敛,则 =】 limun=0. n→c0 证设级数∑u,收敛,且1ims,=5,由于 n=】 Un Sn-Sn-1> 故 lim un lim (Sn-sn-1)=lim sn -lim sn-1=s-s =0. 1→0
第八章 无穷级数 性质 3(级数收敛的必要条件) 如果级数 1 n n u = 收敛,则 lim 0 n n u → = . 证 设级数 1 n n u = 收敛,且lim n n s s → = ,由于 1 , u s s n n n = − − 故 lim lim lim lim 0. n n n n n ( 1 1 ) n n n n u s s s s s s − − → → → → = − = − = − = 二、收敛级数的基本性质