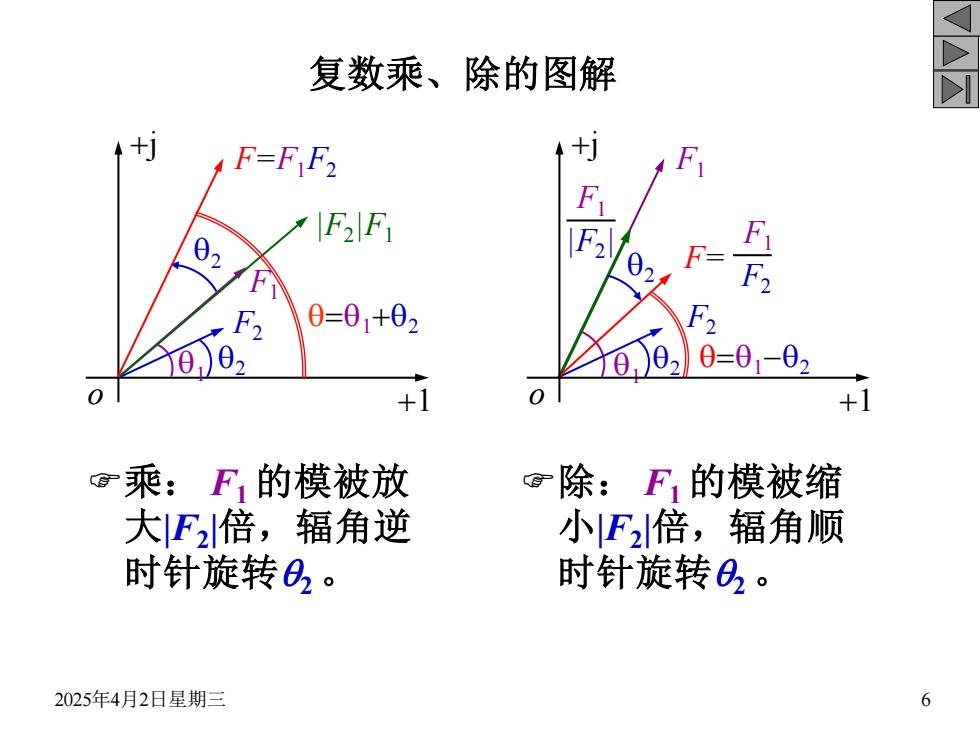
复数乘、除的图解 F=F F2 F F FF 02 F2 F F 02/ F F2 0=01+02 F2 0)02 0=01-02 +1 +1 乘:F的模被放 除:F的模被缩 大F2倍,辐角逆 小F2倍,辐角顺 时针旋转0,。 时针旋转O,。 2025年4月2日星期三 6
2025年4月2日星期三 6 复数乘、除的图解 乘: F1 的模被放 大|F2 |倍,辐角逆 时针旋转q2 。 除: F1 的模被缩 小|F2 |倍,辐角顺 时针旋转q2 。 +j o +1 q1 F1 F2 q2 |F2 |F1 q2 F=F1F2 q=q1+q2 q1 F1 F2 q2 F1 |F2 | q2 F= F1 F2 q=q1-q2 +j o +1
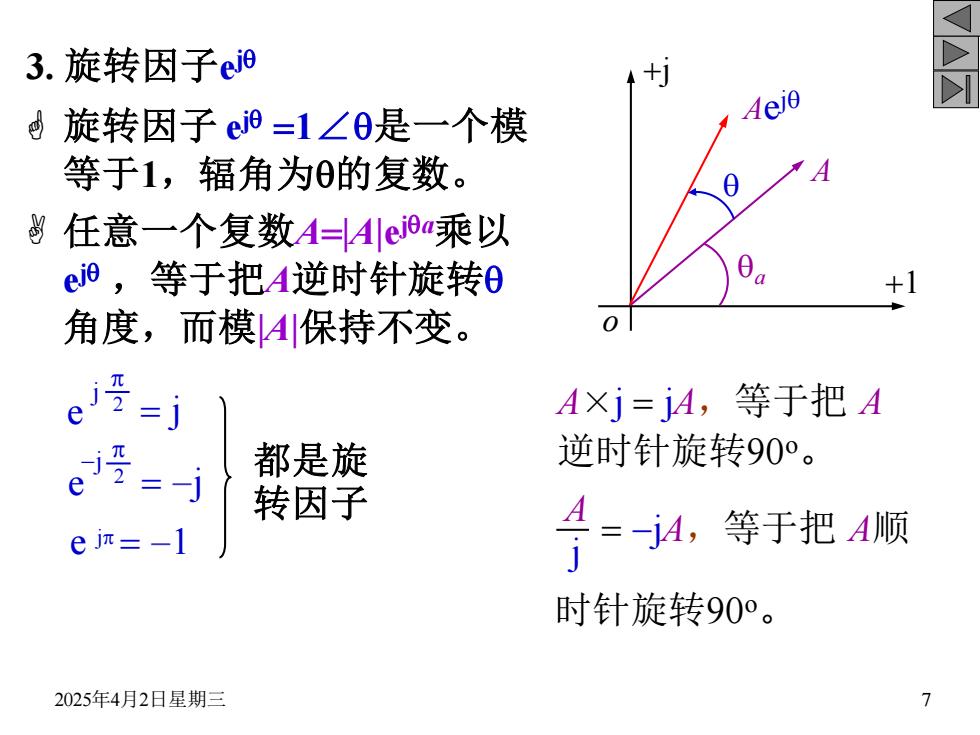
3.旋转因子e 电旋转因子e=1∠0是一个模 等于1,辐角为0的复数。 任意一个复数A=Aeia乘以 e,等于把A逆时针旋转0 +1 角度,而模4保持不变。 受=j e A×j=jA,等于把A 都是旋 逆时针旋转90°。 e" 转因子 ejπ=-1 月=4,等于把4顺 时针旋转90°。 2025年4月2日星期三 1
2025年4月2日星期三 7 3. 旋转因子e jq 旋转因子 e jq =1∠q是一个模 等于1,辐角为q的复数。 任意一个复数A=|A|e jqa乘以 e jq ,等于把A逆时针旋转q 角度,而模|A|保持不变。 +j o +1 A qa Ae jq q 都是旋 转因子 A×j = jA,等于把 A 逆时针旋转90o 。 = -jA,等于把 A顺 A j 时针旋转90o 。 e p 2 = j j e p 2 = -j -j e jp = -1

§8-2正弦量 。电路中按正弦规律变 ②电机、变压器等电气设 化的电压或电流,统 备,在正弦交流电下具 称正弦量。 有较好的性能; ®研究正弦电路的意义 ③正弦量对时间的导数、 是正弦交流电有很多 积分、几个同频率正弦 优点,使它应用广泛。 量的加减,其结果仍是 例如: 同频率的正弦量,这不 ①可以根据需要,利 仅使电路的分析计算变 用变压器方便地把正 得简单,而且其结果还 弦电压升高或降低; 可以推广到非正弦周期 电流电路中。 2025年4月2日星期三
2025年4月2日星期三 8 §8-2 正弦量 电路中按正弦规律变 化的电压或电流,统 称正弦量。 研究正弦电路的意义 是正弦交流电有很多 优点,使它应用广泛。 例如: ①可以根据需要,利 用变压器方便地把正 弦电压升高或降低; ②电机、变压器等电气设 备,在正弦交流电下具 有较好的性能; ③正弦量对时间的导数、 积分、几个同频率正弦 量的加减,其结果仍是 同频率的正弦量,这不 仅使电路的分析计算变 得简单,而且其结果还 可以推广到非正弦周期 电流电路中

正弦量的时域表达式有两种形式 i=Imc0s(ot什) i=Imsin(@+) 也称为瞬时值表达式 分析时不可混用,以免发生相位错误。 采用的形式以教材为准: i=Imcos(@t)u=Umcos(@to) 2025年4月2日星期三
2025年4月2日星期三 9 正弦量的时域表达式有两种形式 i = Imcos(wt+fi ) i = Imsin(wt+fi ) 也称为瞬时值表达式 分析时不可混用,以免发生相位错误。 采用的形式以教材为准: i = Imcos(wt+fi ) u = Umcos(wt+fu )
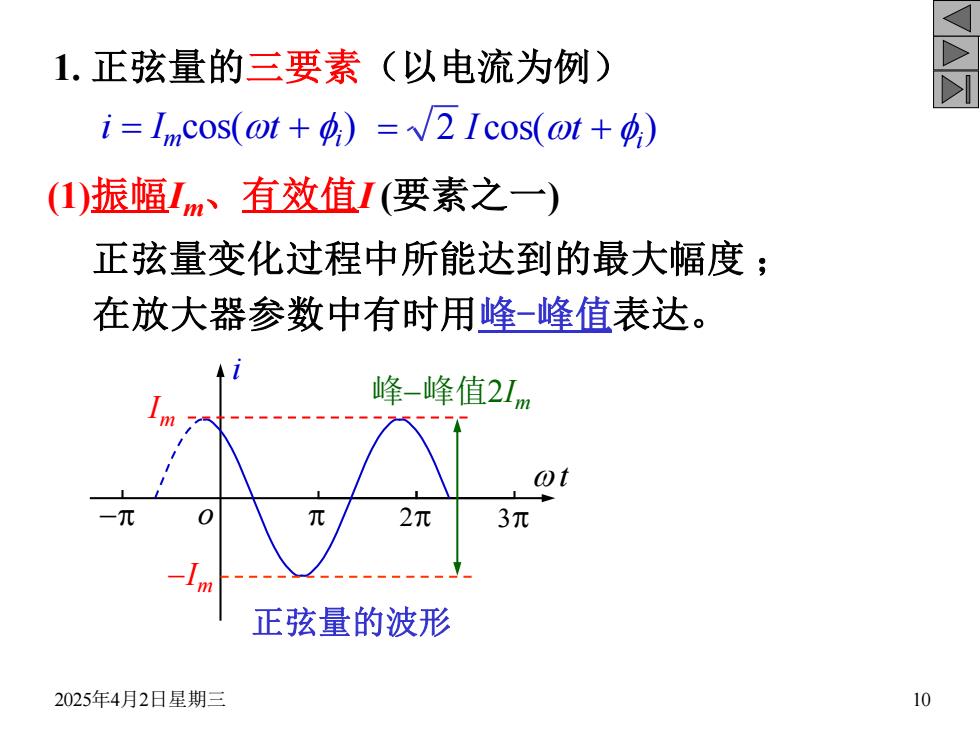
1.正弦量的三要素(以电流为例) i=Im,cos(ot+=2Icos(ot+) (1)振幅Im、有效值I(要素之一) 正弦量变化过程中所能达到的最大幅度; 在放大器参数中有时用峰-峰值表达。 峰-峰值21m ot 2元 3π 正弦量的波形 2025年4月2日星期三 10
2025年4月2日星期三 10 1. 正弦量的三要素(以电流为例) (1)振幅Im、有效值I (要素之一) o i wt -p p 2p 3p 正弦量的波形 Im -Im 在放大器参数中有时用峰-峰值表达。 峰-峰值2Im 正弦量变化过程中所能达到的最大幅度 ; i = Imcos(wt + fi ) = 2 I cos(wt + fi )