点的删除与连通分支数量的增减 ·p(G-V)(其中v是G中任意一个顶点)的情况比较复杂 (注意:删除顶点意味着同时删除该点关联的边) 。 可能会… (孤立点) 。1 减少(删除孤立点) 。不变(例如:删除悬挂点) (悬挂点) 。增加很多个(例如:star)
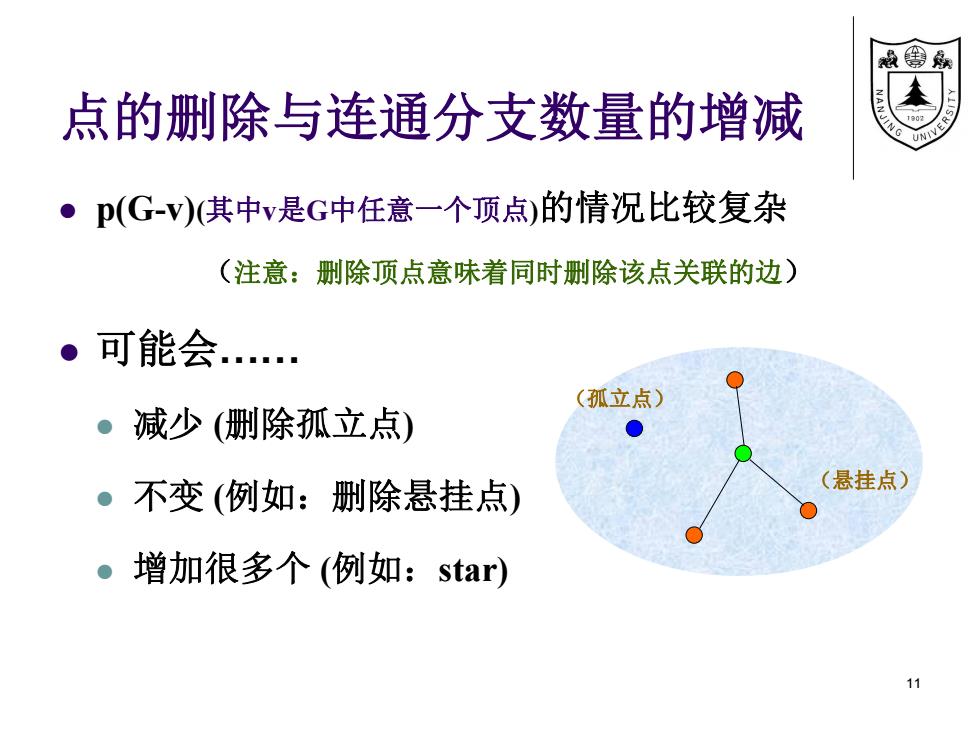
点的删除与连通分支数量的增减 p(G-v)(其中v是G中任意一个顶点)的情况比较复杂 (注意:删除顶点意味着同时删除该点关联的边) 可能会…… 减少 (删除孤立点) 不变 (例如:删除悬挂点) 增加很多个 (例如:star) 11 (孤立点) (悬挂点)
急售康 割点(cut vertex,articulation vertex) ·定义:G是图,v∈Vc若p(G-v)>p(G),则称v是割点 割点 (注意:只需考虑割点所在的连通分支,以下讨论不妨只 考虑连通图) 12
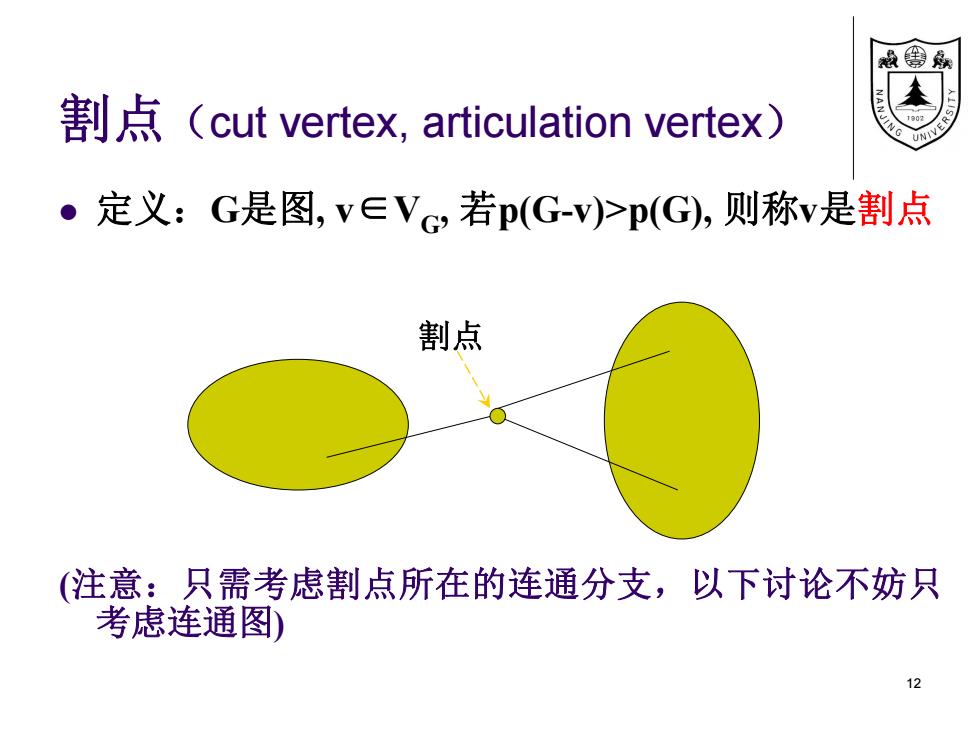
割点(cut vertex, articulation vertex) 定义:G是图, v∈VG , 若p(G-v)>p(G), 则称v是割点 (注意:只需考虑割点所在的连通分支,以下讨论不妨只 考虑连通图) 12 割点

关于割点的三个等价命题 以下三个命题等价: (1)v是割点。 (2)存在V-{w}的分划{V,V,,使u∈V,w∈V,uw-通路均包含v。 (3)存在顶点u,w(uy,w≠y),使得任意的uw-通路均包含v。 ·证明: (1)→(2):.v是割点,G-v至少存在两个连通分支,设其中一个的 顶点集是V1。令V,=V-(V,U{v),则u∈V,w∈V,u,w一定在 G-v的不同的连通分支中。'.在G中,任何uw-通路必含v。 (2)→3):注意:(3)是(2)的特例。 3)→(1):显然,在G-v中已不可能还有uw-通路,∴.G-v不连通, ∴v是割点
关于割点的三个等价命题 以下三个命题等价: (1) v是割点。 (2) 存在V-{v}的分划{V1 , V2 }, 使u∈V1 , w∈V2 , uw-通路均包含v。 (3) 存在顶点u,w(u≠v, w≠v),使得任意的uw-通路均包含v。 证明: (1)(2): ∵v是割点,G-v至少存在两个连通分支,设其中一个的 顶点集是V1。令V2 =V-(V1∪{v}), 则u∈V1 , w∈V2 , u,w一定在 G-v的不同的连通分支中。∴在G中,任何uw-通路必含v。 (2)(3): 注意:(3)是(2)的特例。 (3)(1): 显然,在G-v中已不可能还有uw-通路,∴G-v不连通, ∴v是割点。 13

边的删除与连通分支数量的增加 ●设p(G)表示图G中连通分支数,则: p(G)≤p(G-e)≤p(G)+l,其中e是G中任意一条边 。第一个“不大于”显然成立(删除只会影响e所在的那一 个连通分支)。 。第二个“不大于”成立:注意在图中任意两点之间 加一条边,最多只能将两连通分支连成一个
边的删除与连通分支数量的增加 设p(G)表示图G中连通分支数,则: p(G) p(G-e) p(G)+1, 其中e是G中任意一条边 第一个“不大于”显然成立(删除e只会影响e所在的那一 个连通分支)。 第二个“不大于”成立: 注意在图中任意两点之间 加一条边,最多只能将两个连通分支连成一个。 14
割边(桥;cut edge,bridge) ·定义:设G是图,e∈Ec,若p(G-e)>p(G),则称e是G 中的割边。 割边 (注意:只需考虑割边所在的连通分支,以下讨论不妨只考虑连 通图)
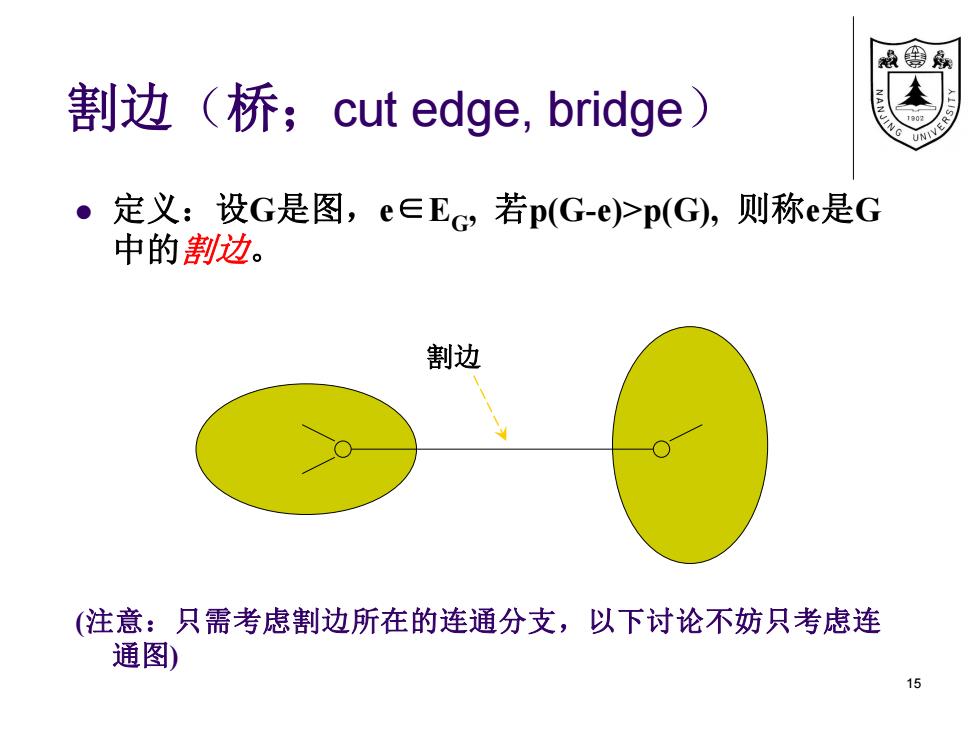
割边(桥;cut edge, bridge) 定义:设G是图,e∈EG , 若p(G-e)>p(G), 则称e是G 中的割边。 (注意:只需考虑割边所在的连通分支,以下讨论不妨只考虑连 通图) 15 割边