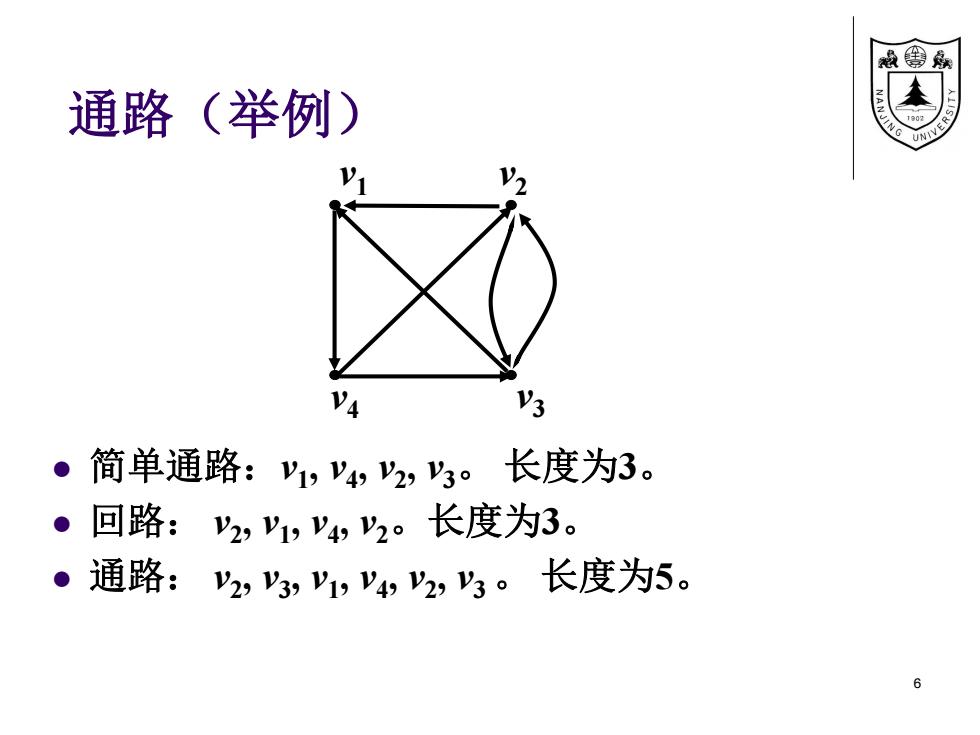
线兔 通路(举例) VA V3 ·简单通路:1,4,2,3。长度为3。 ·回路:2,1,V4,2。长度为3。 ·通路:2,3,1,4,2,3。长度为5。 6
通路(举例) 简单通路:v1 , v4 , v2 , v3。 长度为3。 回路: v2 , v1 , v4 , v2。长度为3。 通路: v2 , v3 , v1 , v4 , v2 , v3 。 长度为5。 6 v1 v2 v v4 3

款嘉 通路与同构 。设图G的邻接矩阵为A ●(A):到y的长度为k的通路个数 ●(A:y到,的长度为k的回路个数 。同构图的不变量:长度为k的回路的存在性
通路与同构 设图G的邻接矩阵为A (Ak )i,j: vi到vj的长度为k的通路个数 (Ak )i,i: vi到vi的长度为k的回路个数 同构图的不变量:长度为k的回路的存在性。 7
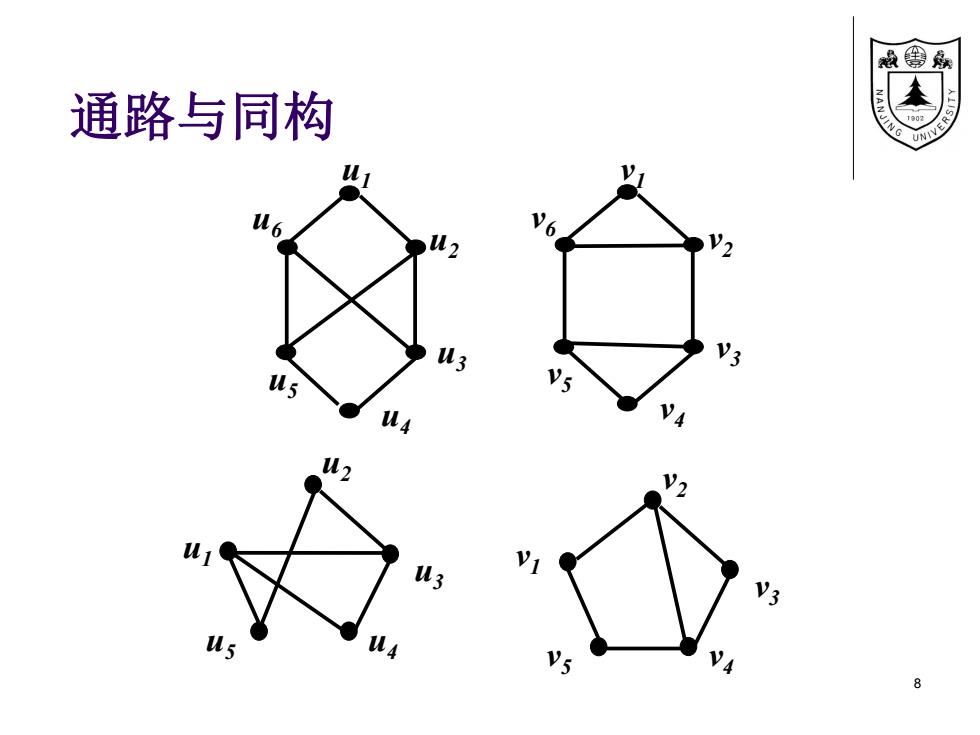
线兔 通路与同构 u3 V: us v5 u3 Vs 8
通路与同构 8 u6 u2 u1 u5 u3 u4 v6 v2 v1 v5 v3 v4 u2 u5 u1 u3 u4 v2 v5 v1 v3 v4
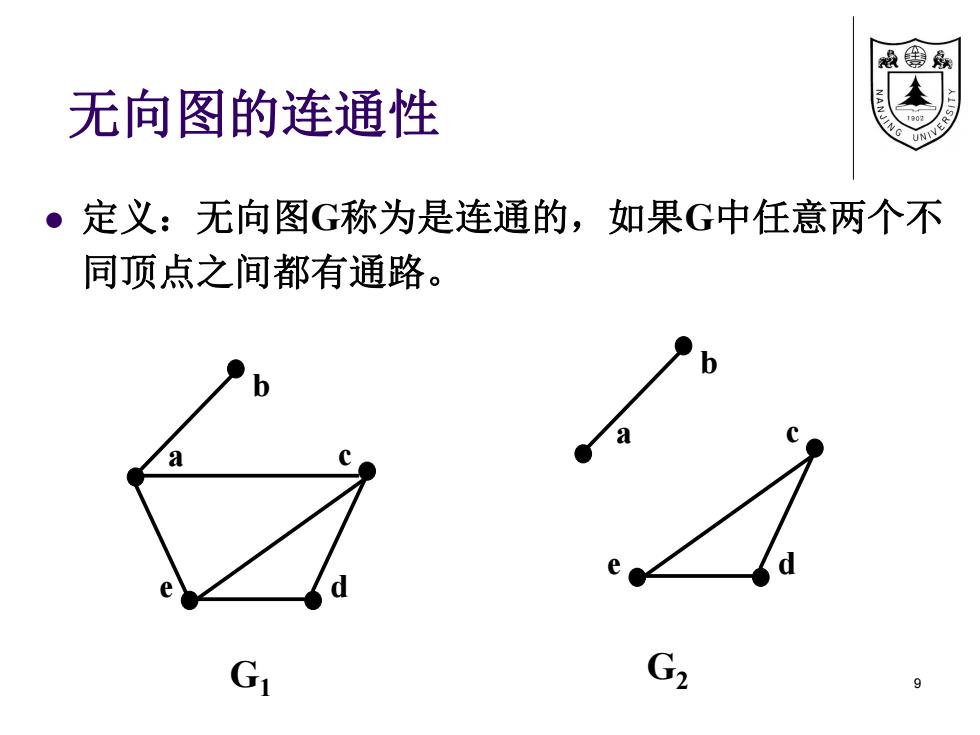
款线嘉 无向图的连通性 。定义:无向图G称为是连通的,如果G中任意两个不 同顶点之间都有通路。 9 G2 9
无向图的连通性 定义:无向图G称为是连通的,如果G中任意两个不 同顶点之间都有通路。 9 a c b e d a c b e d G1 G2

线感 连通分支 ●连通分支 。极大连通子图 。每个无向图是若干个互不相交的连通分支的并。 。“顶点之间存在通路”是一个等价关系,任一等价类上的 导出子图即为一个连通分支。 ●若图G中存在从u到v的通路,则一定有从u到v的简 单通路。 ·证明:最短通路必是简单的,事实上,它没有重复顶点。 10
连通分支 连通分支 极大连通子图 每个无向图是若干个互不相交的连通分支的并。 “顶点之间存在通路”是一个等价关系,任一等价类上的 导出子图即为一个连通分支。 若图G中存在从u到v的通路,则一定有从u到v的简 单通路。 证明:最短通路必是简单的,事实上,它没有重复顶点。 10