
《高等数学A1》课程教学大纲(OBE模式) 一、课程基本信息 1.课程名称 高等数学A1/Advanced Mathematics A1 2.课程代码 13208011 3.课程类别 数理基础课程 4.课程性质 必修 5.学时/学分 885.5 6.先修课程 初等数学 7.后续课程 高等数学A2、概率论与数理统计、复变函数与积分变换、大学物理等 8.适用专业 计算机、通信、光信、电气、机电、自动化、土木、生物、工管、给排水等工科本科各专 业 二、课程的主要任务及目标 1.课程的主要任务 《高等数学A1》课程是高等学校理工科各专业必修的一门重要基础理论课。通过本课 程的学习,要使学生掌握高等数学A1的基本概念、基本理论和基本运算技能,为学习后 继课程和进一步获得数学知识奠定必要的数学基础。要通过各个教学环节逐步培养学生的 抽象思维能力、逻辑推理能力、空间想象能力和自学能力,还要特别注意培养学生的熟练 运算能力和综合运用所学知识去分析解决问题的能力。在讲授该门课程时,应结合应用型 大学数学课程的特点和思政教育的内涵,通过学习数学定义、公式、定理,理解数学思想, 使学生对事物的方法规律有本质的认识,培养学生的辩证唯物主义观。在立足掌握知识的 1

前提下,借助数学发展史、典故以及优秀的数学家奋斗历程等,培养学生不畏艰难、坚持 到底的科学态度和创新精神,同时引导学生学会有效沟通交流,增强其团队合作意识,爱 岗敬业,提高学生的实践能力、创造能力、就业能力和创业能力。 2.课程目标 根据课程的主要任务,现确定高等数学A1课程目标如下: 课程目标1:具备解决工科各类工程有关问题所需的微积分相关基础理论知识。 熟练掌握微积分的相关基础理论知识,培养学生对相关数学概念、定理及一些结论的 理解能力和逻辑推理能力。 课程目标2:具备解决工科各类复杂工程问题所需的计算能力和应用能力。 掌握微积分在工程实际应用中的各种复杂问题的计算方法,初步具备数学模型的建立 的能力、科学分析问题的能力、理论联系工程实际的能力。 三、课程教学内容与学时分配 支 女 序知识单 荐 号元/章节 知识点 教学本麦求 时 教学方式 第节:射与践 :赛及其四种性态。 1、了解涵数的单调性、有界性 奇偶性和周期性:了解反函数 知识点:数列极限定义,收敛数列性质 复合团数、分段函数的概念。了 第三节:教的极限 知识点:函数极限的定义,函数极限的性 解数(数列)极限念,知道 压。 第一章 极限的g-8”、”g-N定 函教与第四节:无穷小与无穷大 义,了解两个极限存在准则以及 18 知识点:无穷小、无穷大的念。 12 极限 第五节:极限运算法侧 初等函数的注续性。 知识点:极限四见运算。 2、理解函数念;熟悉基本礼 第六节:极限存在准测、两个重要极限 等冠数的性质及其阁:能列出 知识点:极限存在准贝测、两个重要极限公 式。 简单实际问题中的函数关系。理 第七节:无穷小的此校 解闭区间上连续数的性质,会
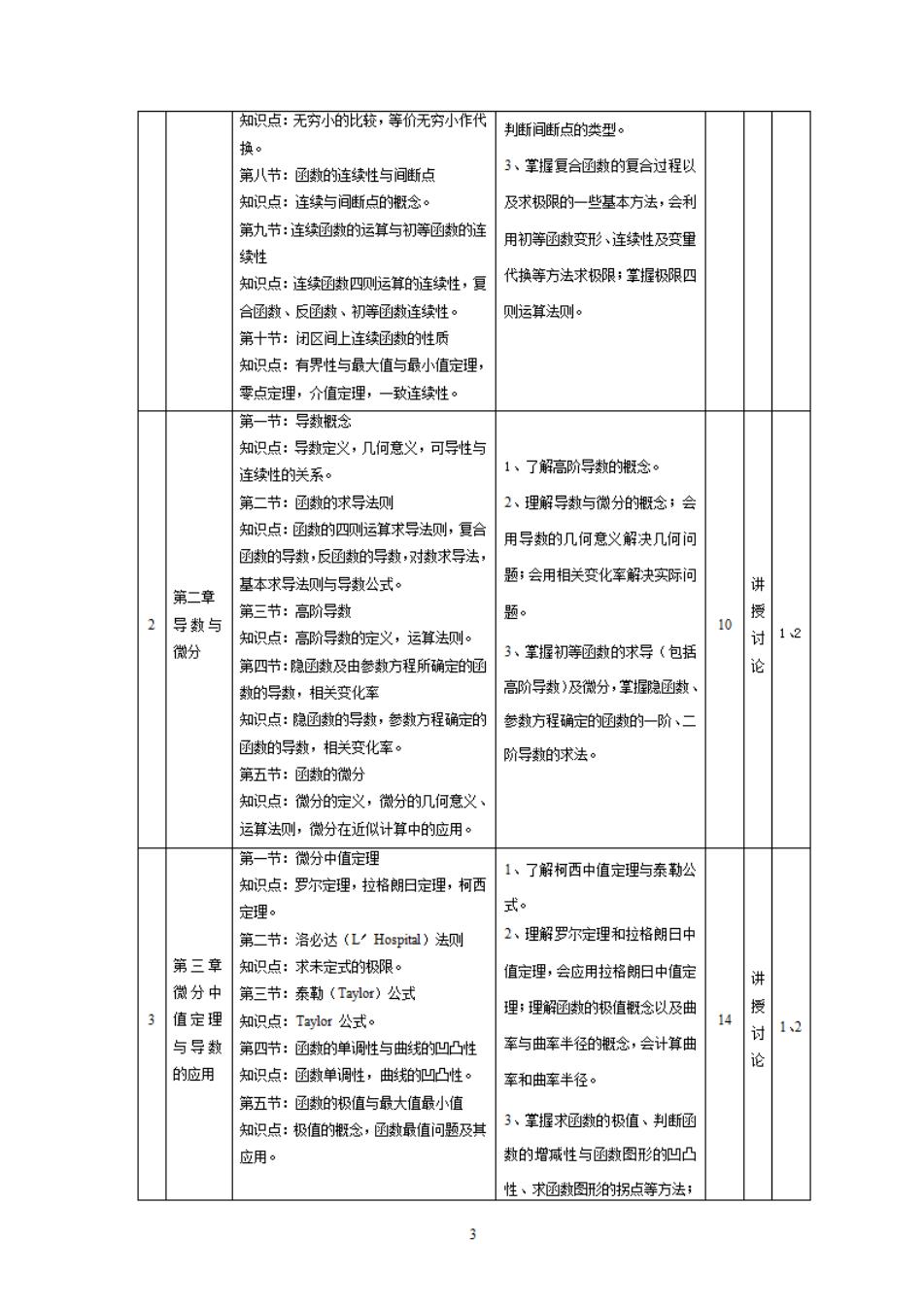
知识点:无穷小的此孩,等价无小作代判断间断点的类型。 推。 第八节:嫩的连续性与间点 3、掌握复合函数的复合过程以 知识点:连续与间点的念。 及求极限的一些基本方法,会利 第九节:连续数的运算与初数的道 用初等通数变形,连续性及变里 续性 知识点:连续数四贝运算的连续性,复 代换等方法求极限:掌握极限四 合函数、反函数、初等承数连续性 运算法则。 第十节:闭区间上连缝承数的性质 知识点:有界性与最大值与最小值定理 零占完理,介值完理,一致连续性。 第一节:导数概念 知识占:导数定义,几间章义,可导性兰 连续性的关系。 1、了解高阶导数的叔念。 第二节:函数的求导法则 2、理解导数与微分的概念:会 知识点:函教的四运算求导法测,复 用导数的几何意义解决几何问 函数的导数,反函数的号数,对数求导法 基本求导法则与导数公式。 题:会用相关变化率解决实际问 第二章 讲 第三节:高阶导数 导数与 微分 知识点:高阶导数的淀义,运算法则。 掌握初等数的求导(包括 第四节:隐函数及由参教方程所确定的还 种的导数,相关变化室 高阶导数)及微分,掌握牌数 知识点:隐数的导数,参数方程确定 参教方程确定的嫩的一阶、二 数的导教,相关变化室 阶导数的求法· 第五节:数的微分 知口占:微的定义,微分的几何意义 运算法则,微分在近似计算中的应用 第一节:微分中值定理 1、了锻柯西中值定甲与泰动公 知识点:罗尔定理,拉格朗日定理,柯西 完理。 第二节:洛必达(LHospital)法 2、理解罗你尔定理和拉格朗日中 第三章 知识占:求未定式的极限。 直定理,会应用拉格朗日中值定 微分中 第三节:泰勒(Taylor)公式 值定理 理:理解的极值念以及曲 3 知识点:Taor公式。 与导数 第四节:函数的单调性与曲线的凹凸性 车与曲车半径的概念,会计算曲 论 的应用 知识点:国嫩单调性,曲的凹凸性 率和曲率半径 第五节:特的极值与最大值最小值 知识点:极值的概念,函数最值问题及其 、掌握求始的极值、判断囝 应用。 数的增减性与函数图形的凹凸 性、术通教图形的拐点等方法;
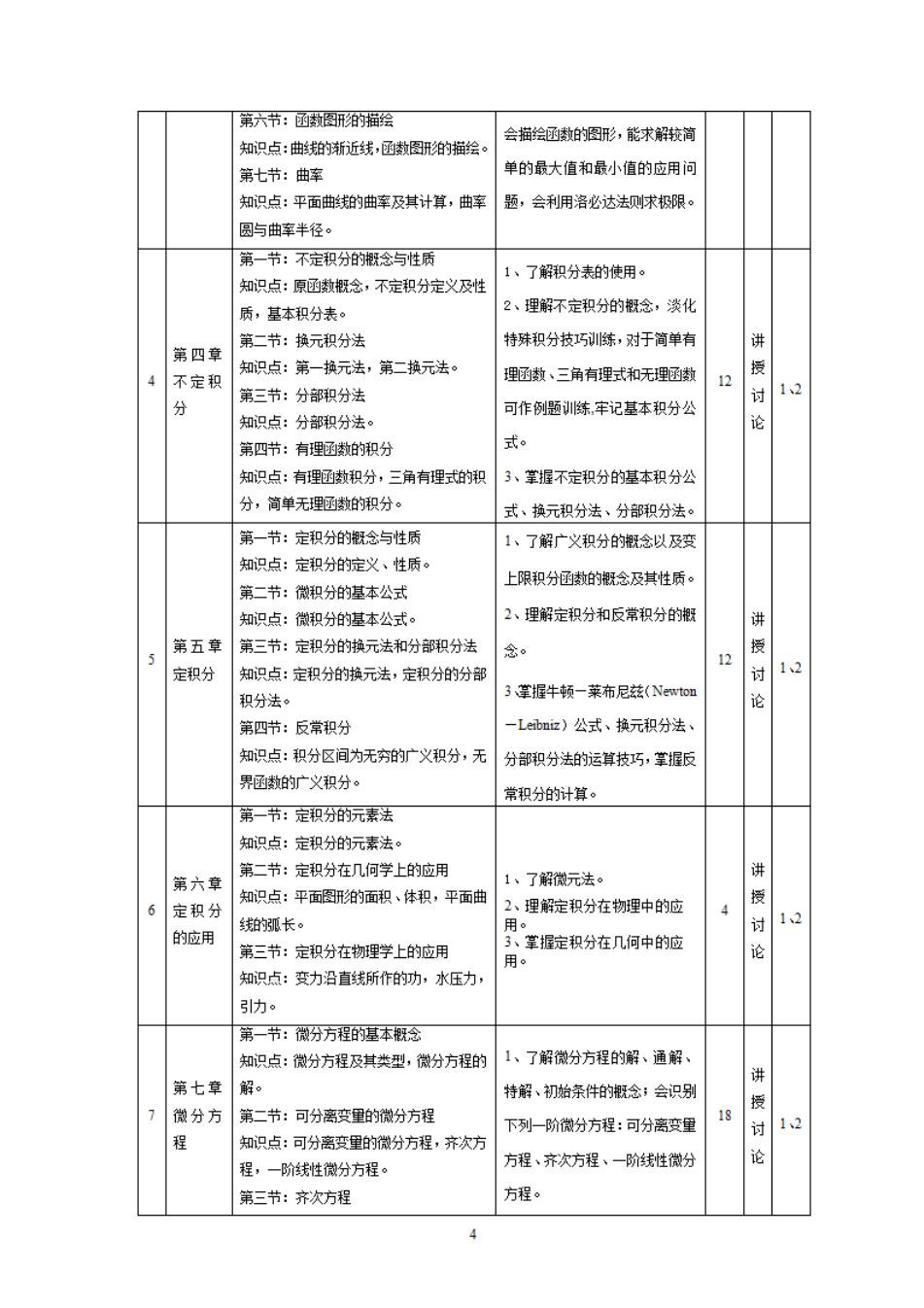
第六节:庭数图肝形阳的描绘 知识点:曲线珀的渐近线,函数图形的描绘。 会描会函的图形,能末解较简 第七节:曲率 单的最大值和最小值的应用问 知识点:平面曲的曲车及其计算,曲率 题,会利用洛必达法求极限 圆与曲率半径。 第一节:不定和分的概今:与性局 知识点:原概念,不定积分定义及性 1、了解积分表的使用。 质,其本和分表。 、理解不定积分的念,淡化 第二节:换元积分法 特殊积分技巧训练,对于简单有 第四章 终 4不定积 知识点:第一换元法,第二换元法。 理函数、三角有理式和无理函数 第三节:分部积分法 可作例题训练牢记基本积分公 知识占:分部积升法。 第四节:有理函数妇的积分 知识点:有用函动积分,三角有理式的和 3、掌握不定积分的基本积分公 分,简单无理函的职分 式、招元积升法、升部和升法。 _节:完和的今与性质 了解广义积分的解念以及变 知识点:定积分的定义、性质 上限积分通的概念及其性质。 第一节:微和分的其本公式 知识点:微积分的螺本公式。 2、理解定积分和反常积分的 第五章第三节:定积分的换元法和分部职分法 念 授 定积分 知识点:定积分的换元法,定积分的分部 12 3堂据牛扬-蒸布尼花(Newto 积分法。 第四节:反常积分 一Leibniz)公式、换元积分法 知识点:积分区间为无穷的广义积分,无 分部积分法的运算技巧,掌握玉 界数的广义积分 常积分的计算 第一节:定积分的元素法 知识点:定和分的元毒法。 第六章 第二节:定积分在几何学上的应用 、了韬微元法。 讲烫 6定积分 知识点:平面图形的面积、体积,平面曲 、理解定积分在物理中的应 的通长 的应用 第三节:定积分在物理学上的应用 室握定积分在几何中的应 用 讨论 知识点:变力沿直线所作的功,水压力 引力。 第一节:微分方程的基本念 知识点:微分方程及其类型,微分方程 1、了解微分方程的解、通解、 第七章 解。 持解、初胎杀件的概念:会识另 微分方 第二节:可分离变里的微分方程 下列一阶微分方程:可分离变里 18 讨 12 知识点:可分离变里的徽分方程,齐次方 程,一阶线性微分方程。 方程、齐次方程、阶线性微分 论 第三节:齐次方程 方程

知识点:齐次方程。 第四节:一阶钱性微分方程 2、理解下列几种特珠的高阶微 知识点:线性微分方程。 分方程:y”=f), 第五节:可降阶的高阶微分方程 y"=f(x.y).y"=f(y.y) 知识点:y同=∫八)型的微分方程, 的降阶法。 y'=f(xy)型微分方程, 3、掌握可分离变里方程、一阶 y”=fy,Jy)型微分方程。 线性微分方程的宋解:会解齐次 第六节:高阶线件微分方程 方程和全微分方程;掌握二阶常 知识点:线性齐次、非齐次方程解的委加 系教线性微分方程的解法;会用 原理,线性齐次非齐次方程通解阳的结构 第七节:常系数齐次线性微分方程 微分方程解一些简单的几何利 知识点:常系数齐次线性微分方程。 物理问题。 第八节:常系数非齐次线性微分方程 知识点:二阶常系数线性幸齐次微分方程 两类型求解。 四、课程教学方式 1.采用启发式教学,激发学生主动学习的兴趣,培养学生独立思考、分析实际问题和 解决实际问题的能力,积极引导学生主动通过实践和自主学习获得相关知识。 2.在教学内容上,按照章节结构系统讲述,重点分析各知识点、定义、定理,强调知 识的应用范围,训练学生的理解能力和计算能力与应用能力。 3.在教学过程中采用多媒体教学与传统板书、救具教学相结合的教学方式,提高课堂 教学信息量,增强教学的直观性。重视课后的习题练习,不定期讲解作业。 4课内讨论和课外答疑相结合,线上线下相结合,灵活使用现代教学技术和手段,如 超星信息化手段。 五、课程的考核环节及课程目标达成度评价方式 (一)课程的考核环节 1.课程考核环节描述 本课程的考核方式为考试,闭卷。课程的考核以考核学生能力培养目标的达成为主要 目的,以检查学生对各知识点的掌握程度和应用能力为重要内容,包括平时考核和期末考 核两个环节,平时考核包括课后作业和到课率,期末考核为期末闭卷考试。相应地,课程 5