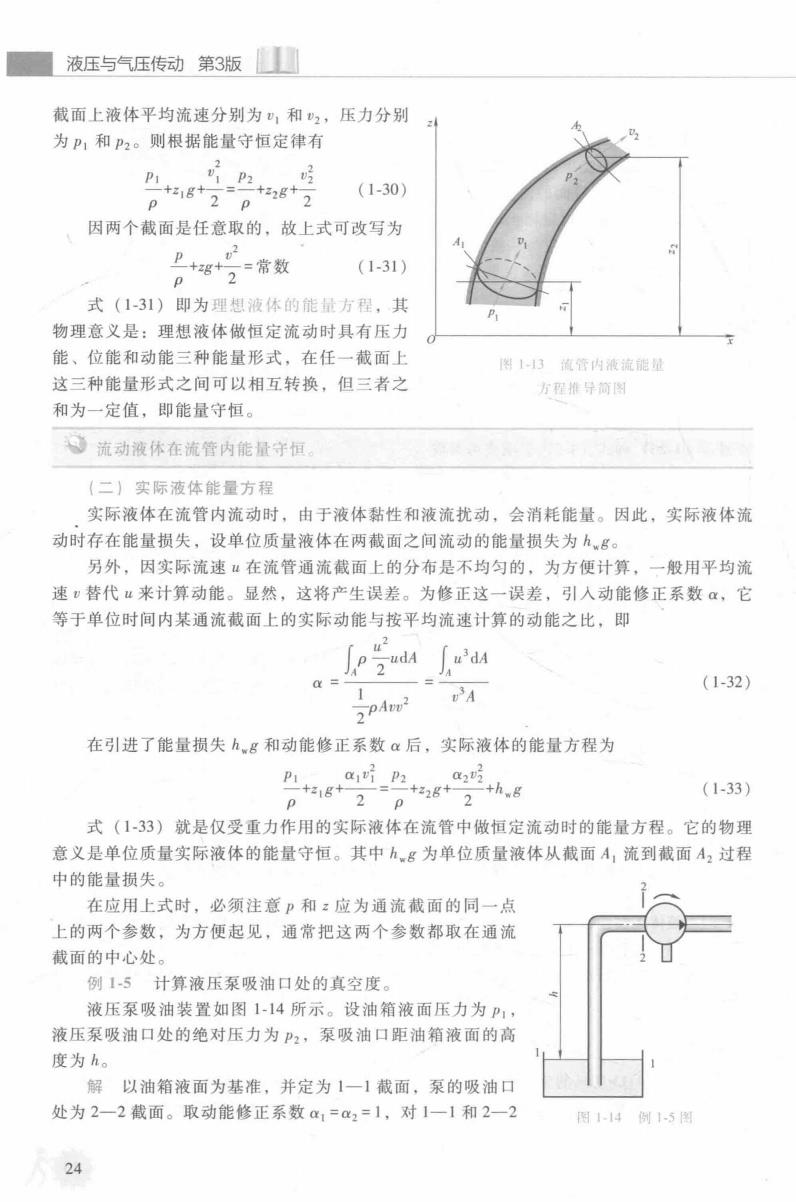
液压与气压传动第3版 截面上液体平均流速分别为1和2,压力分别 z 为P1和P2。则根据能量守恒定律有 +g+2 p =2+2g+2 (1-30) 因两个截面是任意取的,故上式可改写为 2 +g+2常数 (1-31) 式(1-31)即为理想液体的能量方程,其 物理意义是:理想液体做恒定流动时具有压力 能、位能和动能三种能量形式,在任一截面上 附上3流管内液流能地 这三种能量形式之间可以相互转换,但三者之 方程推导简图 和为一定值,即能量守恒。 。流动液休在流管内能量守恒 (二)实际液体能量方程 实际液体在流管内流动时,由于液体黏性和液流扰动,会消耗能量。因此,实际液体流 动时存在能量损失,设单位质量液体在两截面之间流动的能量损失为h8。 另外,因实际流速“在流管通流截面上的分布是不均匀的,为方便计算,一般用平均流 速,替代“来计算动能。显然,这将产生误差。为修正这一误差,引人动能修正系数α,它 等于单位时间内某通流截面上的实际动能与按平均流速计算的动能之比,即 JA a= (1-32) 2p4n2 在引进了能量损失hg和动能修正系数a后,实际液体的能量方程为 -+22g+ (1-33) p 2 P 式(1-33)就是仅受重力作用的实际液体在流管中做恒定流动时的能量方程。它的物理 意义是单位质量实际液体的能量守恒。其中hg为单位质量液体从截面A,流到截面A2过程 中的能量损失。 在应用上式时,必须注意p和z应为通流截面的同一点 上的两个参数,为方便起见,通常把这两个参数都取在通流 截面的中心处。 例15计算液压泵吸油口处的真空度。 液压泵吸油装置如图1-14所示。设油箱液面压力为P1, 液压泵吸油口处的绝对压力为P2,泵吸油口距油箱液面的高 度为h。 解以油箱液面为基准,并定为1一1截面,泵的吸油口 处为2一2截面。取动能修正系数a1=a2=1,对1一1和2一2 图114例15图 24

第一章流体力学基础 截面建立实际液体的能量方程,则有 p+g+2+h.8 P 2 P 图示油箱液面与大气接触,故P1为大气压力,即P1=P。;”,为油箱液面下降速度,由于”,≤ 2,故1可近似为零;2为泵吸油口处液体的流速,它等于流体在吸油管内的流速;h为 吸油管路的能量损失。因此,上式可简化为 Pa P2 p-p thgt 2 thg 所以液压泵吸油口处的真空度为 .Paphtppghpgh 由此可见,液压泵吸油口处的真空度由三部分组成:把油液提升到高度所需的压力、 将静止液体加速到2所需的压力和吸油管路的压力损失。 四、动量方程 动量方程是动量定理在流体力学中的具体应用。用动量方程来计算液流作用在固体壁面 上的力,比较方便。动量定理指出:作用在物体上的合外力的大小等于物体在力作用方向上 的动量的变化率,即 Σr=d业d(m (1-34) dt dt 将动量定理应用于流体时,须在任意时刻1时从流管中取出一个由通流截面A,和A2围 起来的液体控制体积,如图1-15所示。这里,截面A1和 A A2便是控制表面。在此控制体积内取一微小流束,其在 A1、A2上的通流截面为dA1、dA2,流速为u1、u2。假定 控制体积经过dt后流到新的位置A;一A2,则在dt时间内 d 控制体积中液体质量的动量变化为 A d(ΣD=1mm,+l11, (1-35) 0 体积Vm中液体在+dt时的动量为 hw-pu,d1=pu,di,4d 图-15流管内液流动 式中p 液体的密度。 量定理推导简图 同样可推得体积V,中液体在时的动量为 另外,式(1-35)中等号右边的第一、二项为 m山m,三aJ 当d→0时,体积Vm≈V,将以上关系代入式(1-34)和式(1-35),得 25

液压与气压传动第3版 ∑F=)+p,4:dM,-p,udM, 若用流管内液体的平均流速"代替截面上的实际流速“,其误差用一动量修正系数B予 以修正,且不考虑液体的可压缩性,即A=A22=q(而9=厂ud4), 则上式经整理后可 写成 ∑F=(pudW +pg(B22+B1"1】 (1-36) 式中动量修正系数B等于实际动量与按平均流速计算出的动量之比,即 udm u(pudA) 「2da B= (1-37) mu (puA)v 式(1-36)即为流体力学中的动量定理。等式左边ΣF为作用于控制体积内液体上外力 的矢量和:而等式右边第一项是使控制体积内的液体加速(或减速)所需的力,称为瞬态 力,等式右边第二项是由于液体在不同控制表面上具有不同速度所引起的力,称为稳 态力。 稳态液动力和瞬态液动力是液流作用在固体壁面上的两种力 对于做恒定流动的液体,式(1-36)等号右边第一项等于零,于是有 ∑F=pq(B22B11) (1-38) 必须注意,式(1-36)和式(1-38)均为矢量方程式,在应用时可根据具体要求向指定 方向投影,列出该方向上的动量方程,然后进行求解。 若控制体积内的液体在所讨论的方向上只有与固体壁面间的相互作用力,则这两种力大 小相等,方向相反。 例1-6。喷嘴-挡板如图1-16所示。试求射流对挡板的作用力。 解运用动量方程的关键在于正确选取控制体积。在图示情况下,画出abedef为控制体 积,则截面ab、cd、gf上均为大气压力p。。若已知喷嘴出口ab处面积为A,射流的流量为 q,流体的密度为P,并设挡板对射流的作用力为F,由动量方程得 图1-16例1-6图 P.A-F=EF=pq(0-v1)=-pqv 因为P,=0(相对压力),所以 F=pqv=pq2/A 因此,射流作用在挡板上的力大小与F相等,方向向右。 26

第一章流体力学基础 例1-7图1-17所示为一锥阀,锥阀的锥角为20。当液体在压 力p作用下以流量g流经锥阀时,液流通过阀口处的流速为2,出口 压力为P2=0。试求作用在锥阀上的力的大小和方向。 解在图示情况下,取双点画线内部的液体为控制体积。设锥阀 作用在控制体上的力为F,沿液流方向对控制体列出动量方程,则有 pP-fpm(8.cop-B.) 取B1=B2≈1(详见后叙),因1<<2,忽略1,故得 Fpcos 图1-17例1-7图 可见,液流对锥阀作用力的大小等于F,而作用方向与图示方向 相反。 由上述F的计算式可以看出,其中作用在锥阀上的稳态液动力项Pgm2cosp为负值,也 即此力的作用方向应与图示方向一致。因此,在图117情况下, 稳态液动力的方向始终使锥阀阀芯趋于关闭。 例1-8图1-18所示为液压系统的安全阀,阀座直径d= 25mm,当系统压力为5.0MPa时,阀的开度x=5mm,通过的流 量g=600L/min,若阀的开启压力为4.3MPa,油液的密度p= 900kg/m3,弹簧刚度k=20N/mm,试求油液出流角a。 解油液作用在阀上的液压力为 =A1p=4p=4x0.0252x5x10PN=2454.4W 图1-18例1-8图. 弹簧作用在油液上的力为 R.=p+-(x0.025x43x10+20x对小N=210.8N 4 根据动量方程有 Fp-F.-Fp2cosa=Bpq(v2cosa-v1) 由于P2=P.=0(表压),故F2=0,而 4=49=4x600x103/60 m/s=20.4m/s Td2 T×0.0252 3= A2πdxsina 取B=1,则有 Fm-F.=pq qcosa ndxsina π×0.025×0.005 2454.4-2210.8 故 dxFp- cota 一十 +20.4=1.864 600×10-3/60 900×600×10-3/60 则 a=28.20 所以,油流的出流角a为28.2°。 27

液压与气压传动第3版 注:从以上三个例题可以看出,运用动量方程的关键在于正确选取控制体积。 第四节气体状态方程 八一、理想气体状态方程 不计黏性的气体称为理想气体。空气可近似视为理想气体。 一定质量的理想气体在状态变化的某一稳定瞬时,其状态方程为 PV 常数 (1-39 PU=RT (1-40) 式中p—气体绝对压力(Pa): V—气体体积(m3); T一气体的热力学温度(K); 一气体的单位质量体积(m3/kg): R—气体常数[J/(kg·K)],对于干空气,R=287.1J/(kg·K)。 口气体的压力、温度和体积三个参数表征气体处于某种平衡时的状态 二、气体状态变化过程 (一)等容状态过程 在气体的质量、体积保持不变(=常数)的条件下,所进行的状态变化过程,称为等 容过程。状态方程为 片=溶数 (1-41) 在等容过程中,气体对外不做功。气体随温度升高,其压力和内能均增加。 (二)等压状态过程 在气体压力保持不变(=常数)的条件下,一定质量气体所进行的状态变化过程,称 为等压过程。状态方程为 子=常数 (1-42) 在等压过程中,气体的内能发生变化:气体温度升高,体积膨胀,对外做功。 (三)等温状态过程 在气体温度保持不变(T=常数)的条件下,一定质量气体所进行的状态变化过程,称 为等温过程。当气体状态变化很慢时,可视为等温变化过程,如气动系统中的气缸慢速运 动、管道送气过程等。状态方程为 pm=常数 (1-43) 在等温过程中,气体的内能不发生变化,加入气体的热量全部变作膨胀功。 (四)绝热状态过程 在气体与外界无热量交换条件下,一定质量气体所进行的状态变化过程,称为绝热过 28