
第一章流体力学基础 程。当气体状态变化很快时,可视为绝热变化过程,如气动系统的快速充、排气过程。 在绝热过程中,气体靠消耗自身的热能对外做功,其压力、温度和体积三个参数均为变 量。状态方程为 pm*=常数 (1-44) 式中K一等熵指数(又称绝热指数),对于空气,K=1.4。 (五)多变状态过程 在没有任何制约条件下,一定质量气体所进行的状态变化过程,称为多变过程。严格地 讲,气体状态变化过程大多属于多变过程;等容、等压、等温、绝热这四种变化过程不过是 多变过程的特例而已。状态方程为 pw”=常数 (1-45) 式中n一多变指数,对于空气,1.4>n>1,在研究气缸的起动和活塞运动速度时,可取 n=1.2-1.25. 例1-9由空气压缩机向气罐充气,使罐内绝对压力由P1=0.1MPa升高到P2= 0.265MPa,罐内空气温度从室温t1=15℃上升为t2。充气结束后,罐内温度又渐渐降至室 温,空气压力变成p2。已知气源温度t.=15℃,试求2和p值。 解此为一个复杂的状态变化过程,解题时可先视为绝热充气过程,再看作等容降温 过程。 1)由绝热过程状态方程式(1-44),有P1=p2,经转换后得 /0.265 =(273+15)× K=380.5K 0.1 所以 t2=T2-273℃=(380.5-273)℃=107.5℃ 2)充气结束后为等容降温过程,罐内气体的温度由T1=380.5K降到T=(15+273)K, Pi P2 压力从P听=0,265MP降至P吃,根据等容过程状态方程式(1-41),有分疗所以 T 15+27 P2=PIT =0.265× MPa=0.2MPa 380.5 三、气体流动基本方程 前面已指出,当气体流速较低时,流体运动学和动力学的三个基本方程,对于气体和液 体是完全相同的。但当气体流速较高(>5m/s)时,气体的可压缩性将对流体运动产生较 大影响。下面介绍在这种情况下的气体流动基本方程。 (一)可压缩气体的流量方程 根据质量守恒定律,气体在管道内做恒定流动时,单位时间内流过管道任一通流截面的 气体质量都相等。因此,可压缩气体的流量方程为 p1A,1=p2A22 (1-46) 式中p1、P2一截面1、2处气体的密度: 29

液压与气压传动第3版 A1、A2—截面1、2的面积: 1、2一截面1、2处气体的平均流速。 (二)可压缩气体的能量方程 若不计能量损失和位能变化,则绝热过程下可压缩气体的能量方程为 KP1听KP2吃 (1-47) K-1P12K-1P22 式中K一等嫡指数。其余符号意义同式(146)。 同理,多变过程中可压缩气体的能量方程为 npn pa (1-48) n-1P12m-1P22 式中n一多变指数。 第五节充、放气参数的计算 在气压传动系统中,如何正确合理地向气罐、气缸及执行机构充气或由其排气,是提高 系统效率、节省能耗的重要技术问题。本节介绍充、放气时温度和时间的计算方法。 一、向定容容器充气 如图1-19所示,压力为P,、温度为T,的恒定气源,通过气动元件(图中为气阀)向容 积V一定的容器内充气。容器内的压力和温度从P1和T,升高到 P2和T2。因充气较快,热量来不及通过容器壁面向外界传导, 故充气过程可按绝热过程处理。 根据气体状态方程可推得充气后的温度T,(单位为K)为 T2= K T (1-49) 1+ 图119向容器充气 式中一等嫡指数,K=1.4。 当气源的温度T,与容器的初始温度T,都是室温,即T.=T时,则 72= KT (1-50) P1 t2(-1) 1+ 由式(1-50)可知,绝热充气时,无论充气后容器内的压力多么高,其气体的温度T2 都不会超过气源温度T.的1.4倍。 如果容器充气完毕后,立即关闭气阀,在温差作用下,容器内气体将通过壁面向外散 热,温度再次降至室温T,此时容器内的气体压力也要下降到一定值,根据气体状态方程, 则有 T P=P2T2 (1-51) 式中P一充气后,温度又降到室温时,容器内气体的稳定压力值。 30
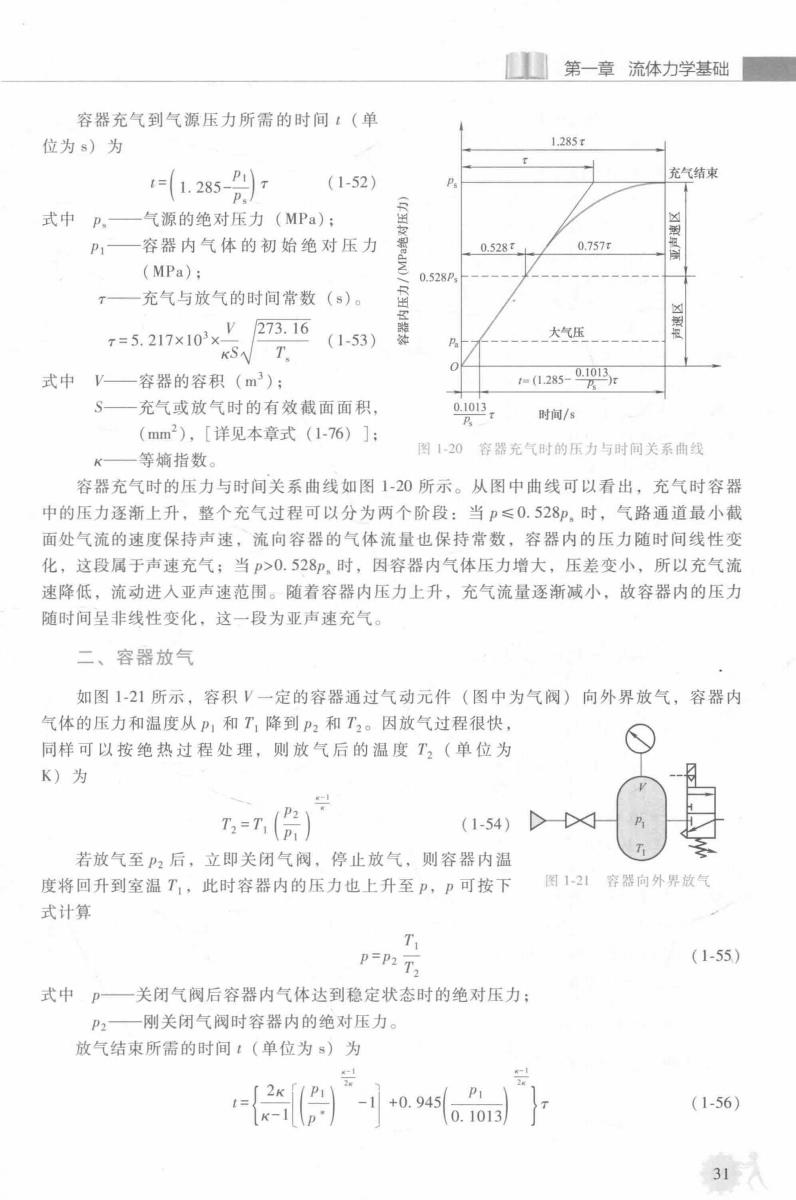
第一章流体力学基础 容器充气到气源压力所需的时间1(单 位为s)为 1.285t 1.285P四7 (1-52) 充气结束 P. 式中P,一气源的绝对压力(MPa): 容器内气体的初始绝对压力 0.528t 0.757x (MPa) 0.528P 一充气与放气的时间常数(s)。 273.16 7=5.217×103× (1-53) 大气压 KS T. 式中V—容器的容积(m3): 1(1.285-01013 S一充气或放气时的有效截面面积, 0.1013 A 时间/s (mm2),[详见本章式(1-76)]: 图120容器充气时的压力与时间关系曲线 K一 等熵指数。 容器充气时的压力与时间关系曲线如图1-20所示。从图中曲线可以看出,充气时容器 中的压力逐渐上升,整个充气过程可以分为两个阶段:当p≤0.528即,时,气路通道最小截 面处气流的速度保持声速,流向容器的气体流量也保持常数,容器内的压力随时间线性变 化,这段属于声速充气;当p>0.528即,时,因容器内气体压力增大,压差变小,所以充气流 速降低,流动进入亚声速范围。随着容器内压力上升,充气流量逐渐减小,故容器内的压力 随时间呈非线性变化,这一段为亚声速充气。 二、容器放气 如图1-21所示,容积V一定的容器通过气动元件(图中为气阀)向外界放气,容器内 气体的压力和温度从P1和T,降到P2和T2。因放气过程很快, 同样可以按绝热过程处理,则放气后的温度T2(单位为 K)为 =(片】 (1-54) 若放气至P2后,立即关闭气阀,停止放气,则容器内温 度将回升到室温T,此时容器内的压力也上升至P,p可按下 图1-21容器向外界放气 式计算 T P=P2T2 (1-55) 式中一关闭气阀后容器内气体达到稳定状态时的绝对压力: P2一刚关闭气阀时容器内的绝对压力。 放气结束所需的时间1(单位为s)为 +0.945 P (1-56) 0.1013 31
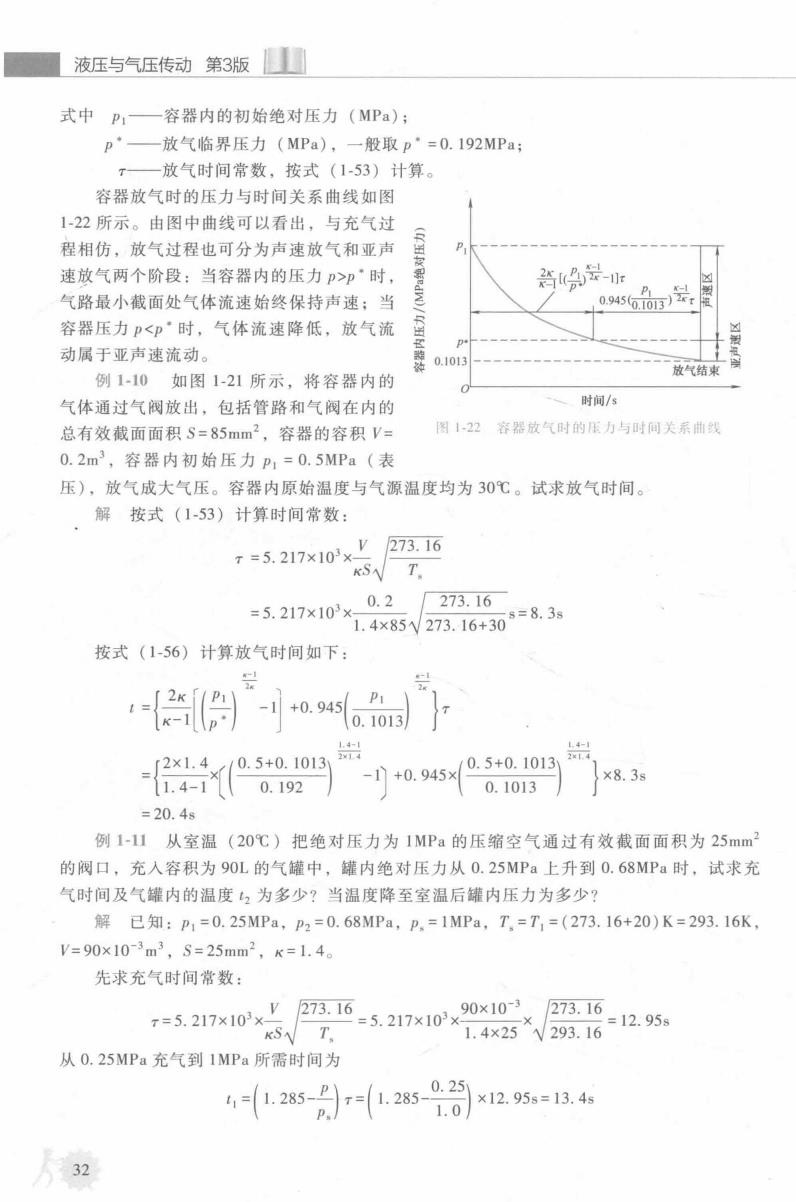
液压与气压传动第3版 式中pP1一容器内的初始绝对压力(MPa); p·一放气临界压力(MPa),一般取p·=0.192MPa; T—放气时间常数,按式(1-53)计算。 容器放气时的压力与时间关系曲线如图 1-22所示。由图中曲线可以看出,与充气过 程相仿,放气过程也可分为声速放气和亚声 P 速放气两个阶段:当容器内的压力P>p·时, 高是- P 气路最小截面处气体流速始终保持声速:当 0.945603)2r 容器压力p<p·时,气体流速降低,放气流 动属于亚声速流动。 放气结束 例1-10如图1-21所示,将容器内的 气体通过气阀放出,包括管路和气阀在内的 时间/s 总有效截面面积S=85mm2,容器的容积V= 图122容器放气时的压力与时间关系曲线 0.2m3,容器内初始压力p1=0.5MPa(表 压),放气成大气压。容器内原始温度与气源温度均为30℃。试求放气时间。 ,解按式(153)计算时间常数: V 273.16 T=5.217×103× KS T 0.2 273.16 =5.217×103× 1.4×85√273.16+303=8.38 按式(1-56)计算放气时间如下 +0.945 0.1013 4- 2x1.4 2×1.4 0.5+0.1013 0.5+0.1013y 1.4- -1+0.945× ×8.3s 0.192 0.1013 =20.4s 例1-11从室温(20℃)把绝对压力为1MPa的压缩空气通过有效截面面积为25mm2 的阀口,充人容积为90L的气罐中,罐内绝对压力从0.25MPa上升到0.68MPa时,试求充 气时间及气罐内的温度2为多少?当温度降至室温后罐内压力为多少? 解已知:p1=0.25MPa,p2=0.68MPa,p,=1MPa,T,=T1=(273.16+20)K=293.16K, V=90×10-3m3,S=25mm2,k=1.4。 先求充气时间常数: 7=5217x103xy 273.16 =5.217×103× 90×10-3 273.16 =12.95s KS T. 1.4×25W293.16 从0.25MPa充气到1MPa所需时间为 41.28512545 ×12.95s=13.4s 32

第一章流体力学基础 从0.68MPa充气到IMPa所需时间为 =1.285-0.68 ×12.95s=7.835s 1.0 从0.25MPa充气到0.68MPa所需时间为 t=t1-2=(13.4-7.835)s=5.565s 按绝热过程计算充气后罐内温度为 KT T2= 1.4×293.16K=357.8K 0.25 2(K-1)1 ×(1.4-1) P2 0.68 即 t2=(357.8-273.16)℃=84.6℃ 按等容过程计算降至室温后罐内空气压力为 B=P万0.68 293.1 MPa=0.56MPa 357.8 第六节管道流动 本节讨论液体流经圆管及各种管道接头时的流动情况,进而分析流动时所产生的能量损 失,即压力损失。液体在管中的流动状态直接影响液流的各种特性,所以先要介绍液流的两 种流态。 一、流态与雷诺数 (一】层流和湍流 19世纪末,英国物理学家雷诺首先通过实验观察了水在圆管内的流动情况,发现液体 有两种流动状态:层流和湍流。实验结果表明,在层流时,液体质点互不干扰,液体的流动 呈线性或层状,且平行于管道轴线;而在湍流时,液体质点的运动杂乱无章,除了平行于管 道轴线的运动外,还存在着剧烈的横向运动。 层流和湍流是两种不同性质的流态。层流时,液体流速较低,质点受黏性制约,不能随 意运动,黏性力起主导作用:湍流时,液体流速较高,黏性的制约作用减弱,惯性力起主导 作用 (二)雷诺数 液体的流动状态可用雷诺数来判别。 雷诺数可用来判别液体的流动状态,它是一个由液体的平均流速、运动黏度和管径军 个参数组成的无量纲数 实验证明,液体在圆管中的流动状态不仅与管内的平均流速有关,还和管径d、液体 的运动黏度v有关。而用来判别液流状态的是由这三个参数所组成的一个称为雷诺数R的 无量纲数 vd Re=- (1-57) 33