
基础自主梳理 温馨提示 1.圆的内部的点可以看作是到圆心的距离小于半径的,点的 集合;圆的外部的点可以看作是到圆心的距离大于半径的点 的集合 2.点和圆的位置关系的判断方法的逆命题也都成立,于是可 以知道: (1)d心r台,点在圆外; (2)d=r台,点在圆上; 3)d<r台点在圆内. 导航页
导航页 基础自主梳理 温馨提示 1.圆的内部的点可以看作是到圆心的距离小于半径的点的 集合;圆的外部的点可以看作是到圆心的距离大于半径的点 的集合. 2.点和圆的位置关系的判断方法的逆命题也都成立,于是可 以知道: (1)d>r⇔点在圆外; (2)d=r⇔点在圆上; (3)d<r⇔点在圆内

核心重难探究 知识点:点与圆的位置关系 【例题】如图,已知矩形ABCD的边AB=3cm,BC=4cm,以 点A为圆心,4cm为半径作⊙A,则点B,C,D与⊙A有怎样的位 置关系? B 思路点拨:连接 根据勾股定理求出 的 长,即可得出点B,C,D与⊙A的位置关系. 导航页
导航页 核心重难探究 知识点:点与圆的位置关系 【例题】如图,已知矩形ABCD的边AB=3 cm,BC=4 cm,以 点A为圆心,4 cm为半径作☉A,则点B,C,D与☉A有怎样的位 置关系? 思路点拨:连接 ,根据勾股定理求出 的 长,即可得出点B,C,D与☉A的位置关系
核心重难探究 解:连接AC,.四边形ABCD是矩形, ..AD-BC. .AB=3 cm,BC=AD=4 cm, .AC=VAB2+BC2=V32+42=5(cm). .·⊙A的半径是4cm, .‘.点B在⊙A内,点D在⊙A上,点C在⊙A外. 导航页
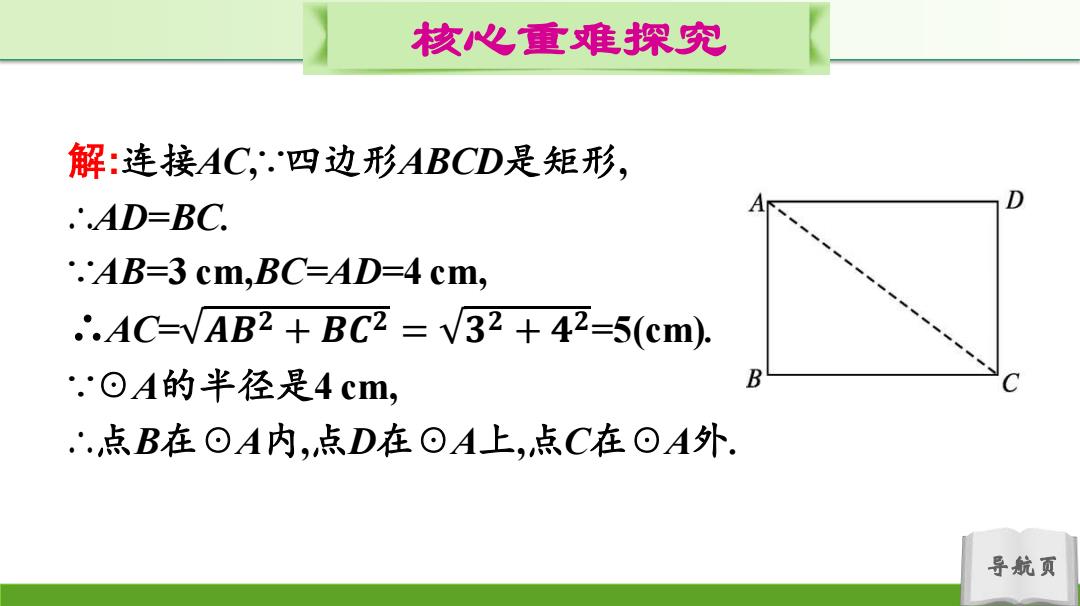
导航页 核心重难探究 解:连接AC,∵四边形ABCD是矩形, ∴AD=BC. ∵AB=3 cm,BC=AD=4 cm, ∴AC= 𝑨𝑩𝟐 + 𝑩𝑪𝟐 = 𝟑𝟐 + 𝟒𝟐 =5(cm). ∵☉A的半径是4 cm, ∴点B在☉A内,点D在☉A上,点C在☉A外