3.2测试输入信号与时域性能指标(t)tymar1.瞬态响应性能±(c0)My(o)1)上升时间tr:从终值10%上升到终值90%所需时间:振荡系y(oo)统定义为从零第一次上升到终值所需时间。曲线第一次达到2)延迟时间td:终值一半所需时间3)峰值时间t,:响应到达第一个峰值所需时间。4)调节时间t:到达并保持在终值+/-5%误差内所需最短时间5)最大超调量%(简称超调量):最大偏离量M,与终值y(0)的百分比。响应曲线在同方向上相邻两个波峰的偏离量之比6)衰减比ng:M= y(t)- y(o0)y(t,)- y(o0)D5% =x100%x100% (4-1) ny(0)y(t3) - y(00)y(o)
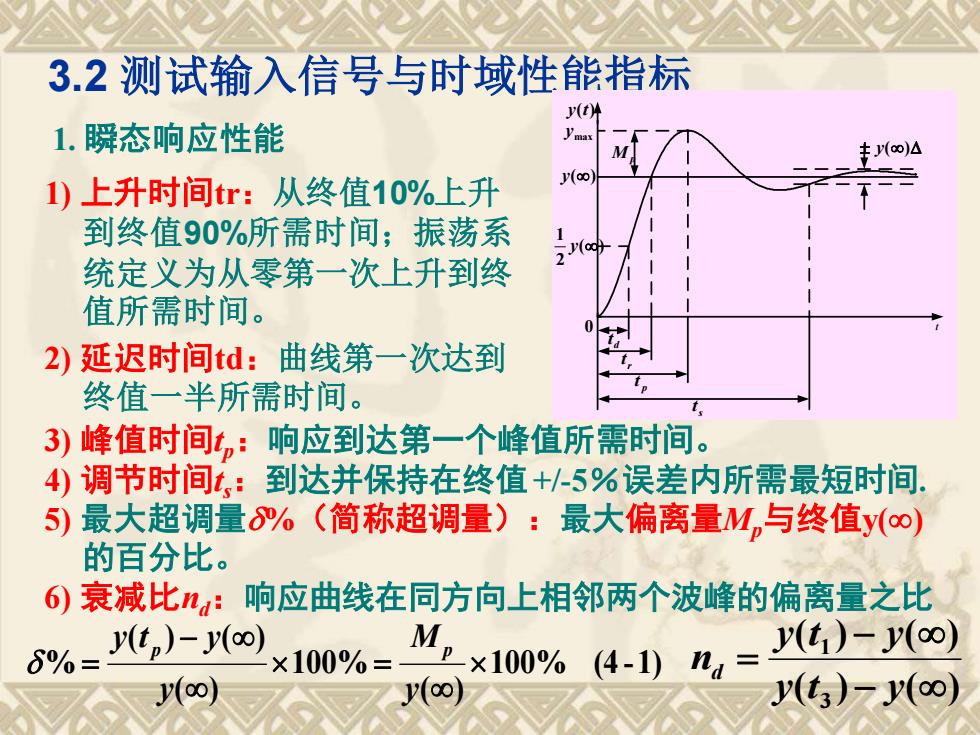
3.2 测试输入信号与时域性能指标 1) 上升时间tr:从终值10%上升 到终值90%所需时间;振荡系 统定义为从零第一次上升到终 值所需时间。 2) 延迟时间td:曲线第一次达到 终值一半所需时间。 3) 峰值时间tp:响应到达第一个峰值所需时间。 4) 调节时间t s:到达并保持在终值+/-5%误差内所需最短时间. 5) 最大超调量%(简称超调量):最大偏离量Mp与终值y() 的百分比。 6) 衰减比nd:响应曲线在同方向上相邻两个波峰的偏离量之比 100% (4 -1) ( ) 100% ( ) ( ) ( ) % = − = y M y y t y p p ( ) ( ) ( ) ( ) 3 1 − − = y t y y t y nd t y(t) 0 ( ) 2 1 y y() max y y() d t rt p t s t Mp 1. 瞬态响应性能

3.2测试输入信号与时域性能指标7)振荡次数:指响应曲线在调节时间内偏离稳态值振荡的次数:若振荡周期为TS,则振荡次数Ns=ts/Ts:2.稳态响应性能指标R(s) E(s)Y(s)+Gk(s)从输入端定义,系统误差定义为e(t)=r(t)-b(t) (3-2)B(s)H(s)稳态误差:ess = e(t) lt-0 = e(00)两种定义之间尽管数值可以不从输出端定义:若同,但经过传感器或测量装置系统误差=输出期望值一实际值量纲换算后是完全等价的。e(t)= y。(t)-y(t) (3-3)稳态误差:e=é(t)lt-=é()本书采用第一种定义方法
3.2 测试输入信号与时域性能指标 7) 振荡次数:指响应曲线在调节时间内偏离稳态值振荡的 次数;若振荡周期为Ts,则振荡次数Ns=ts/Ts . e(t) = r(t)-b(t) (3- 2) 从输入端定义,系统误差定义为: 2. 稳态响应性能指标 = ( )| = () → e e t e s s t 稳态误差: ( ) ~ ( )| ~ ~ ( ) ( ) ( ) (3-3) ~ s s = t = = − = − → e e t e e t y t y t o 稳态误差: 系统误差 输出期望值 实际值, 从输出端定义:若 R(s) E(s) H(s) Y(s) G (s) k B(s) 两种定义之间尽管数值可以不 同,但经过传感器或测量装置 量纲换算后是完全等价的。 本书采用第一种定义方法
3.3一阶系统的时域分析3.3.1一阶系统的一般形式R(s)Y(s)1T dy(0)KTs+ y(t)= Kr(t) (3- 4)dtT:描述系统惯性的时间常数1Y(s)传递函数K:对输入信号进行放大的放大系数Ts +1R(s)由图(a)可见,要研究系统内部的本质,只需研究系统的单位阶跃或单位脉冲等函数的响应即可,不失一般jos平面地可考虑K=1。3.3.2一阶系统的单位阶跃响应单位阶跃响应:01T11R(s) =Y(s)(3-6)三Ts +1Ts +1s(Ts + 1)ST1= L-'[Ys(s)+Y(s)]= ys(t)-y(t) =1-e-1/T, t≥0y(t)= L(3-7)Ts +1S
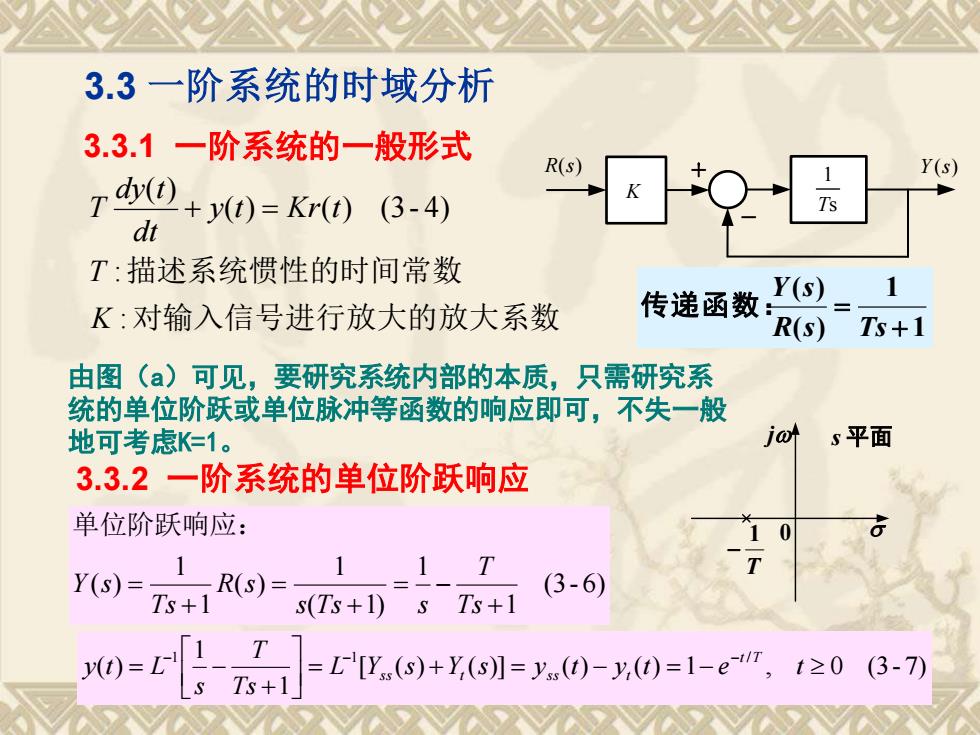
3.3 一阶系统的时域分析 3.3.1 一阶系统的一般形式 对输入信号进行放大的放大系数 描述系统惯性的时间常数 : : ( ) ( ) (3 - 4) ( ) K T y t K r t dt dy t T + = 1 1 ( ) ( ) + = R s Ts Y s 传递函数: (3 - 6) 1 1 ( 1) 1 ( ) 1 1 ( ) + = − + = + = Ts T s Ts s R s Ts Y s 单位阶跃响应: [ ( ) ( )] ( ) ( ) 1 , 0 (3- 7) 1 1 ( ) 1 1 / = + = − = − + = − − − − L Y s Y s y t y t e t Ts T s y t L t T s s t s s t 3.3.2 一阶系统的单位阶跃响应 j T 1 − s 平面 0 s 1 T R(s) K Y(s) 由图(a)可见,要研究系统内部的本质,只需研究系 统的单位阶跃或单位脉冲等函数的响应即可,不失一般 地可考虑K=1
初始斜率!J(t)43.3一阶系统的时域分析T3.3.2一阶系统的单位阶跃响应稳态分量:ss(t)=10.9820.95瞬态分量: y,(t)=-e-t/T0.8650.6321)以无因次时间=t/T取++T2T3T4T0不同值时的输出1)一阶系统单位阶跃响应的tr、t。和ty(0)=1-e,均正比于时间常数。y(T) = 1- e-1 = 0.632,t=2.20T,t=0.69T,t=3T或4T(4=0.05或0.02)y(2T) =1- e-2 = 0.865,2)时间常数越大,系统的惯性越大响应过程越长,反之,系统的惯性越小,响应过程越快。y() = 12)当=1,2,3,,8时,响应曲线斜率dy(t)1dy(t)dy(t)dy(t)1=0.368=0=0.135T'TFdtdtdtdt=0(=Tt=2Tt=00
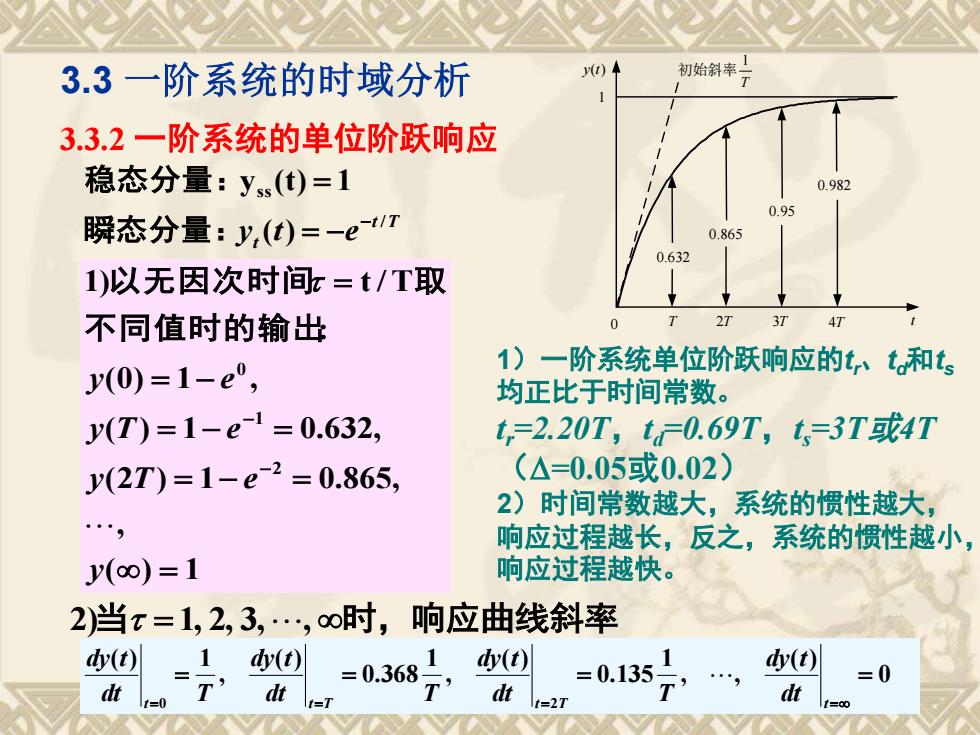
3.3 一阶系统的时域分析 t T t y t e / ss ( ) y (t) 1 − = − = 瞬态分量: 稳态分量: ( ) 1 , (2 ) 1 0.865, ( ) 1 0.632, (0) 1 , : 1) t / T 2 1 0 = = − = = − = = − = − − y y T e y T e y e 不同值时的输出 以无因次时间 取 2)当 = 1, 2, 3, , 时,响应曲线斜率: 0 ( ) , , 1 0.135 ( ) , 1 0.368 ( ) , ( ) 1 0 2 = = = = t= t=T t= T t= dt dy t dt T dy t dt T dy t dt T dy t 1)一阶系统单位阶跃响应的tr、td和ts 均正比于时间常数。 t r=2.20T,td=0.69T,t s=3T或4T (=0.05或0.02) 2)时间常数越大,系统的惯性越大, 响应过程越长,反之,系统的惯性越小, 响应过程越快。 3.3.2 一阶系统的单位阶跃响应 T 2T 3T 4T t 0 y(t)1 0.632 0.865T 1 初始斜率 0.95 0.982
3.3一阶系统的时域分析3.3.3一阶系统的单位脉冲响应t)1/T1Y(s(3-8)RTs + 1Ts +110.368/T-t/Tt≥0(3-9)V1T0.135/TV0.050/T0.018/T3二===三华以无因次时间t=t/T取2TT3T4T0不同值时的输出1只有瞬态分量而没有稳态分量2)另外,时间常数T越小,系统y(T) = 0.368y(0) :响应的快速性越好,反之,响应过程增长。福y(2T) = 0.135y() = 0T0.368dy(t)dy(t)dy(t)0.135dy(t)= 0TTTdtdtdtdt0T=1T=2T=00
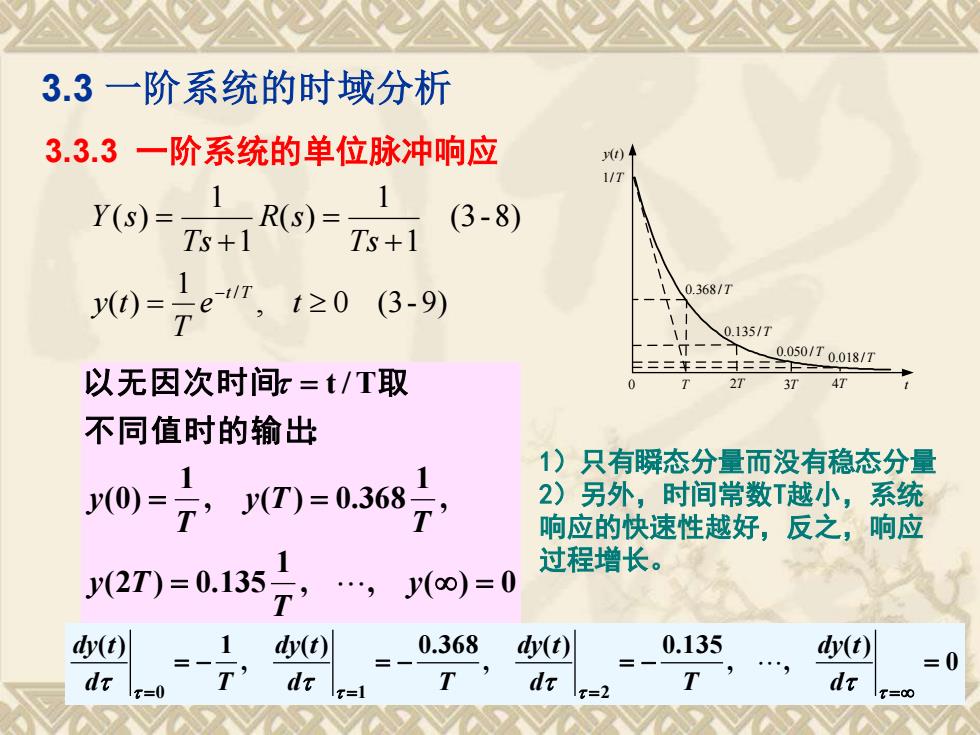
3.3 一阶系统的时域分析 3.3.3 一阶系统的单位脉冲响应 (3-8) 1 1 ( ) 1 1 ( ) + = + = Ts R s Ts Y s , 0 (3-9) 1 ( ) / = − e t T y t t T , , ( ) 0 1 (2 ) 0.135 , 1 , ( ) 0.368 1 (0) : t / T = = = = = y T y T T y T T y 不同值时的输出 以无因次时间 取 0 ( ) , , ( ) 0.135 , ( ) 0.368 , ( ) 1 0 1 2 = − = − = − = = = = = d d y t d T d y t d T d y t d T d y t 1)只有瞬态分量而没有稳态分量 2)另外,时间常数T越小,系统 响应的快速性越好,反之,响应 过程增长。 0 T 2T 3T 4T t y(t) 1/T 0.135 /T 0.368 /T 0.050 /T 0.018/T