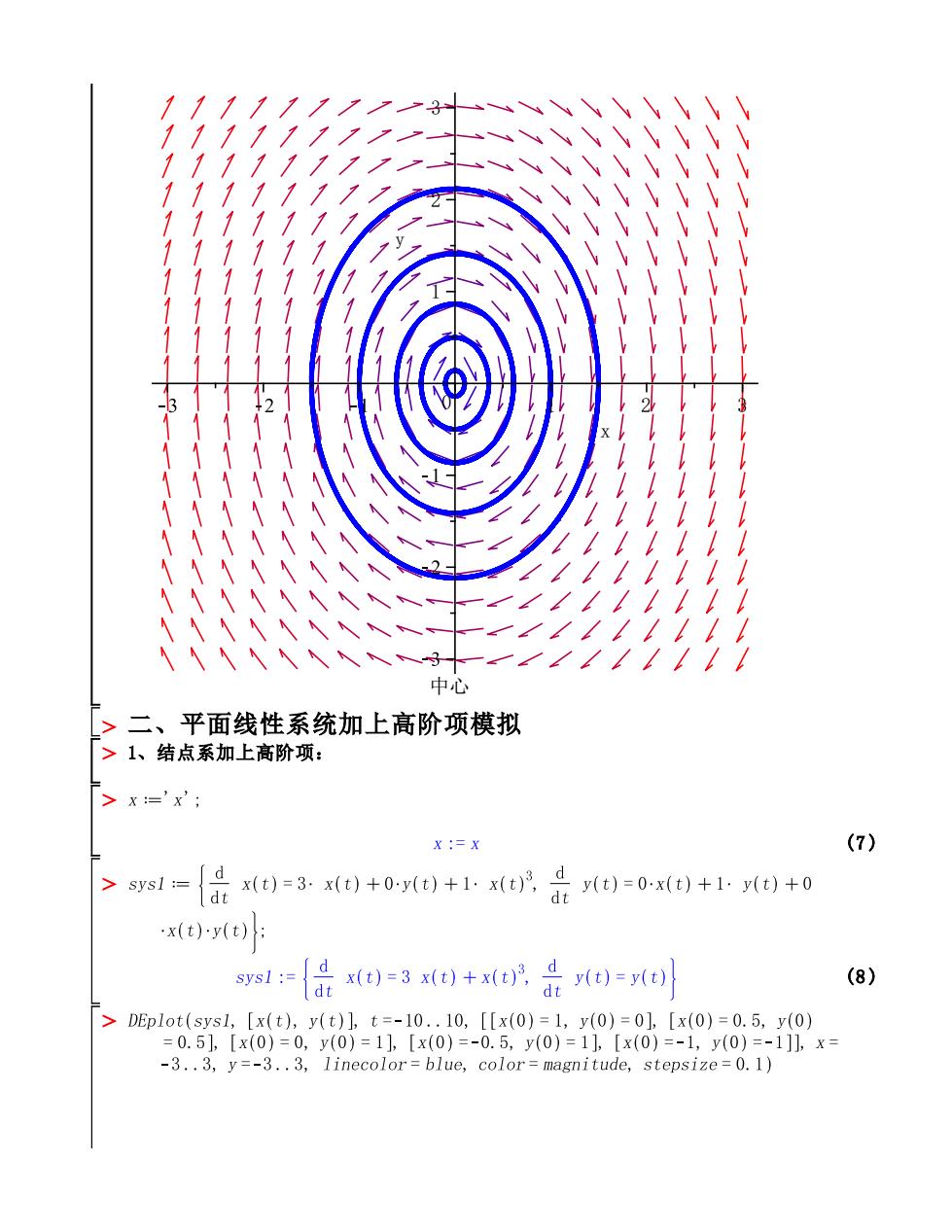
3 中心 >二、平面线性系统加上高阶项模拟 >1、结点系加上高阶项: >x='x; (7) {[品e=30+0-+1是)=0)+1)+0 x(t)小y(t) d 0=3x0+识品e= d (8) >DEplot(sysl,[x(t,y(t)],t=-10.10,[x(0)=1,y(0)=0],[x(0)=0.5,y(0) 1[x(0) 0,y(0)=1[x(0 =-0.5,(0)=1[x0)=-l,y0 -1],x .3.y=-3..3.linecolor=blue,color=magnitude,stepsize
(7) (8) x 0 1 2 3 y 1 2 3 中心 二、平面线性系统加上高阶项模拟 1、结点系加上高阶项:
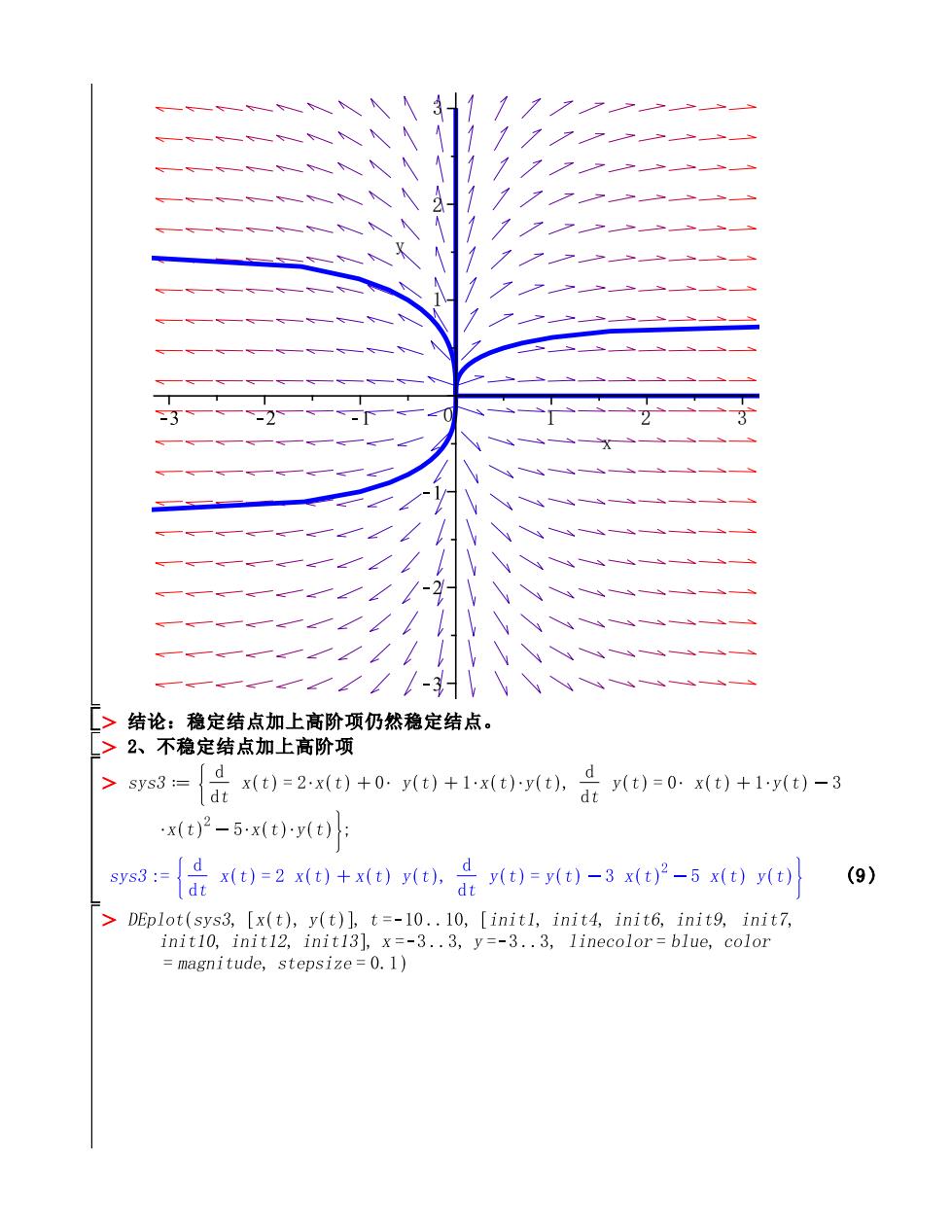
[>结论:稳定结点加上高阶项仍然稳定结点。 >2、不稳定结点加上高阶项 >sys3={是x)=2x(t)+0:y)+1xt)y(t),是)=0:)+1y()-3 ]dt x(t)2-5x(t)小y(t): 3:品)=2)+0是)=)-3-5 (9) dt DEplot(sys3,[x(t),y(t)],t=-10..10,[initl,init4,init6,init9,init7, init10,init12,init13],x=-3..3,y=-3..3,linecolor=blue,color magnitude,stepsize=0.1)
(9) x 0 1 2 3 y 1 2 3 结论:稳定结点加上高阶项仍然稳定结点。 2、不稳定结点加上高阶项

>结论:不稳定结点加上高阶项仍为不稳定结点。 L>3、鞍点系加上高阶项 sys5:= =-2x)+3+0-x-,是=0-)+1)+ 「d x(t小y(t) sys5:= 0)=-2x+明是0)=0+0 (10) DEplot(sys5,[x(t),y(t)],t=-10..10,[initl,init7,init10,init9,initll, init12,init5,[x(0)=-0.5,y(0)=-0.1],[x(0)=1,y(0)=0.5]l,x=-3.3,y= -3..3,linecolor=blue,color=magnitude,stepsize=0.1)
(10) x 0 1 2 3 y 1 2 3 结论:不稳定结点加上高阶项仍为不稳定结点。 3、鞍点系加上高阶项
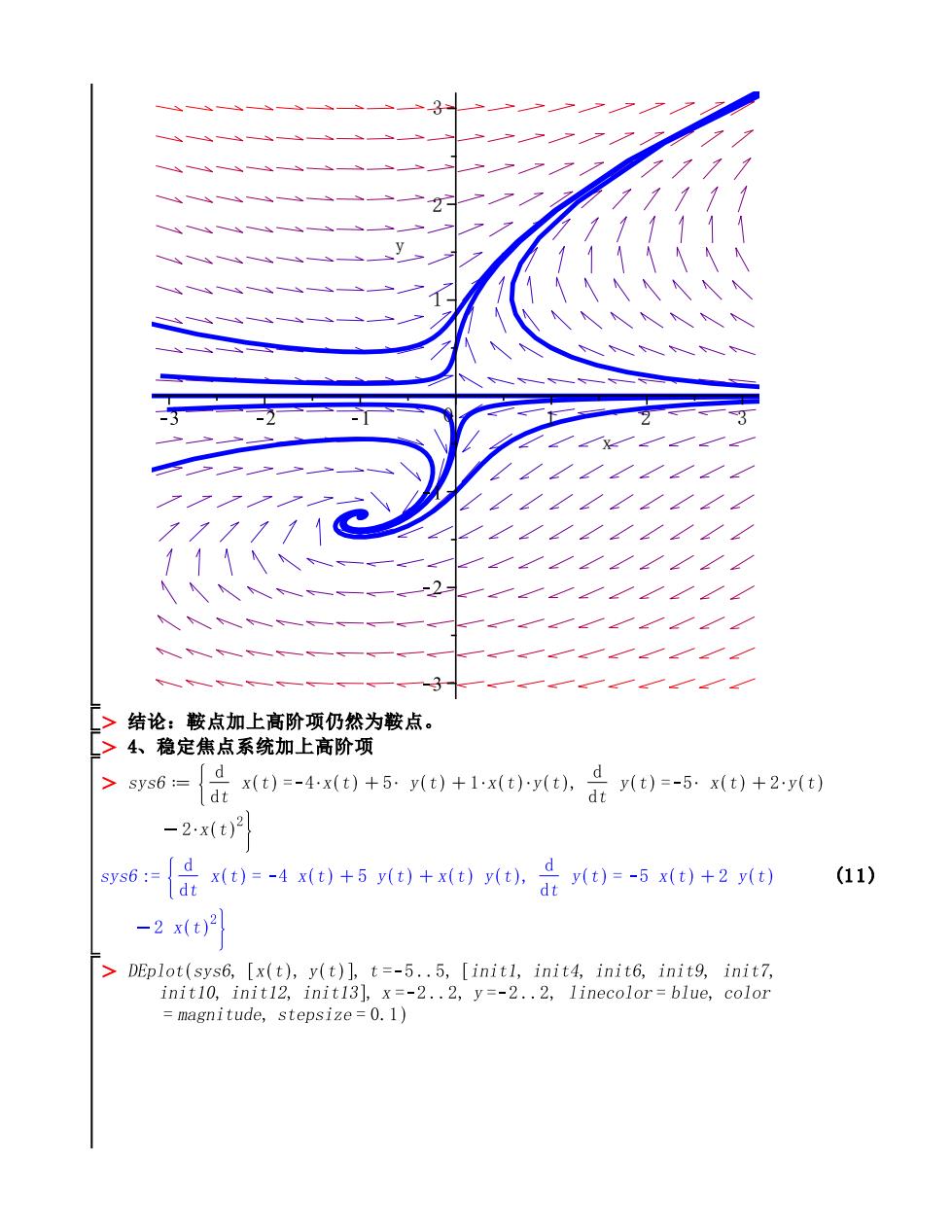
>结论:鞍点加上高阶项仍然为鞍点。 L>4、稳定焦点系统加上高阶项 >ss6={品x=-4t)+5)+1t)yt.)=-5X)+2e) ]dt -2x(t)2 ss6={倍)=4x+50+0e是)=-5u+2 (11) -2x(t)2 DEplot(sys6,[x(t),y(t)],t=-5..5,[initl,init4,init6,init9,init7, init10,init12,init13],x=-2..2,y=-2..2,linecolor=blue,color magnitude,stepsize=0.1)
(11) x 0 1 2 3 y 1 2 3 结论:鞍点加上高阶项仍然为鞍点。 4、稳定焦点系统加上高阶项
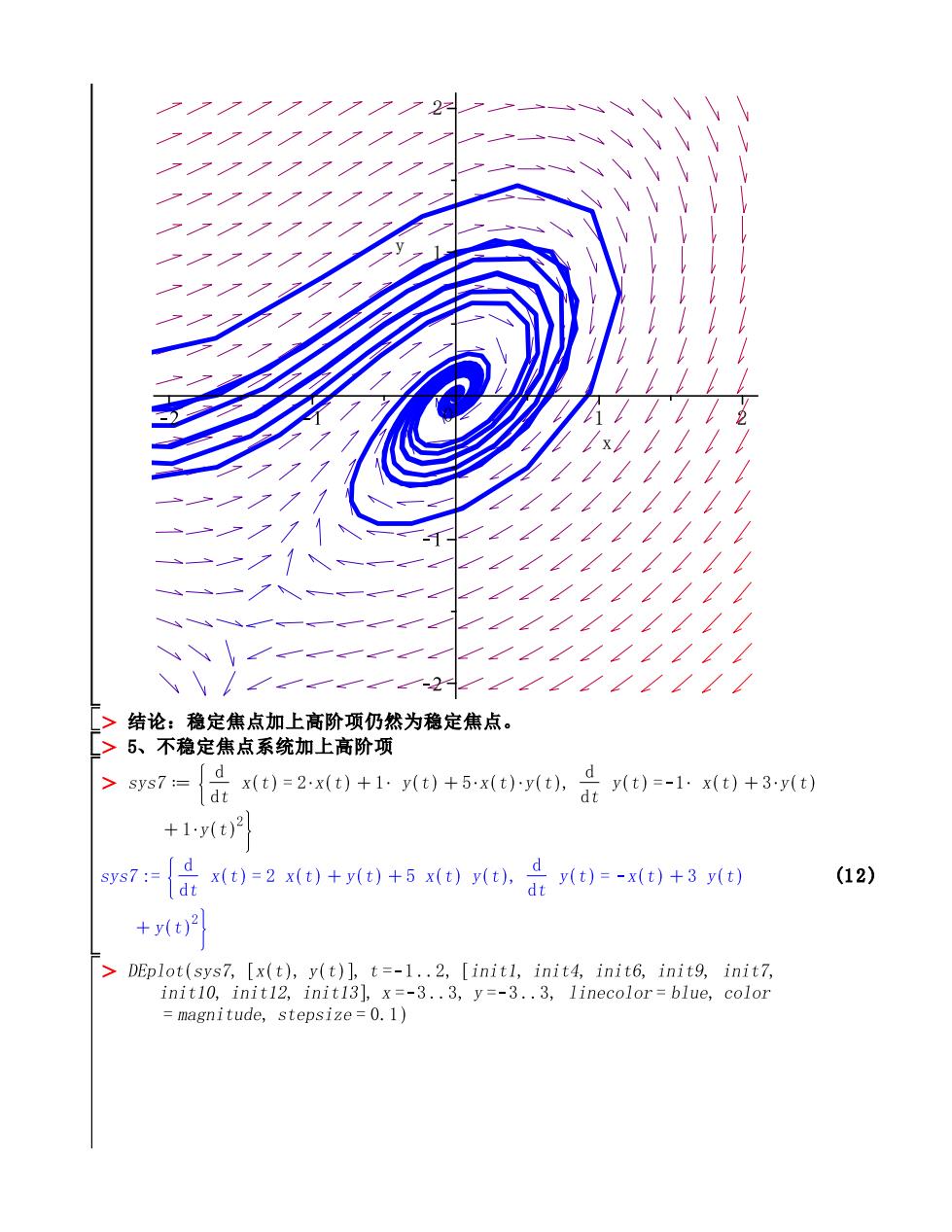
-2 >结论:稳定焦点加上高阶项仍然为稳定焦点。 [>5、不稳定焦点系统加上高阶项 >s7={品)=2,)+)+5y.是t=-小t)+3y +1yt)2 ys7:xt)=2x+y+5x),)=-xe)+3) (12) dt +y(t)2 DEplot(sys7,[x(t),y(t)],t=-1..2,[initl,init4,init6,init9,init7, init10,init12,init13],x=-3..3,y=-3..3,linecolor=blue,color magnitude,stepsize=0.1)
(12) x 0 1 2 y 1 2 结论:稳定焦点加上高阶项仍然为稳定焦点。 5、不稳定焦点系统加上高阶项