X=XL+Xc 0L-I +UR C .=arctg R Ux ④当R=0,X>0时,Z为纯电感性; ⑤当R=0,X<0时,Z为纯电容性。 gRLC串联电路的电压UR、 Ux UU构成电压三角形。 X 满足:U=VU+U及 p R 11
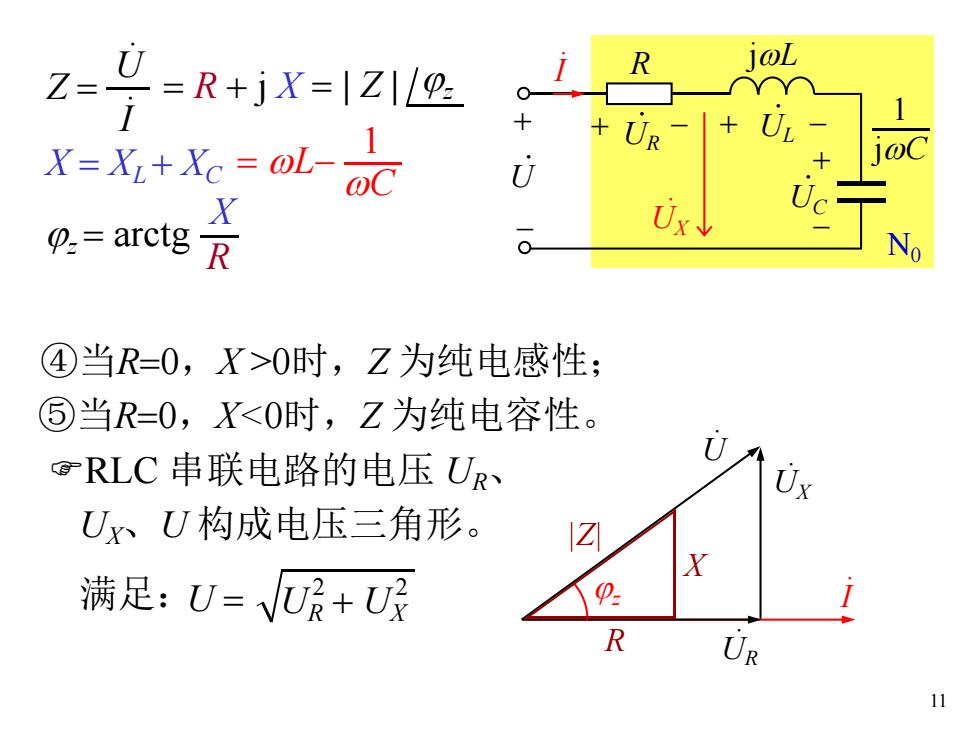
11 ④当R=0,X >0时,Z 为纯电感性; FRLC 串联电路的电压 UR、 UX、U 构成电压三角形。 满足:U = UR + UX 2 2 .I . UR .U jz . UX |Z| X R ⑤当R=0,X<0时,Z 为纯电容性。 + - + - R jwL + - . UR . UL . UC jwC 1 + - . U .I N0 Z = .I .U = R + j X = | Z | jz = wL- wC 1 X = XL + XC jz = arctg R X . UX

2.导纳Y (①)阻抗Z的倒数定义为导纳,即:Y=之 ”=吉-名他鱼=川@m位是s Ⅵ=7 称为导纳模,也可以简称为导纳。 r=中-功。称为导纳角。 >导纳的代数形式为:Y=G+jB 实部G称为电导,虚部B称为电纳。 导纳三角形 >G、B、YI、pr之间的关系为 G=Ycospy IY=VG2+B2 B B=Ysiny Py py=arctg G 12
12 2. 导纳 Y (1)阻抗Z的倒数定义为导纳Y, 即:Y = 1 . Z I Y = . fi-fu = |Y| jY [单位是S] U = I U 也可以简称为导纳。 jY =fi-fu 称为导纳角。 |Y| = Ø 导纳的代数形式为: Y = G + j B 实部G称为电导,虚部B称为电纳。 ØG、B、|Y|、jY 之间的关系为 G=|Y|cosjY B=|Y|sinjY jY | Y | G B 导纳三角形 |Y| = G2 + B2 jY = arctg G B I 称为导纳模, U
(2)单个R、L、C元件的导纳 当无源网络内为单个元件 时,等效导纳分别为: ®纯电阻 Y- 称为电导: 纯电感 Y= i =jBL jol BL=- 称为感性电纳: 微纯电容 Y= =joC=jBc Y可以是纯实 U 数,也可以是 Bc=oC称为容性电纳; 纯虚数。 13
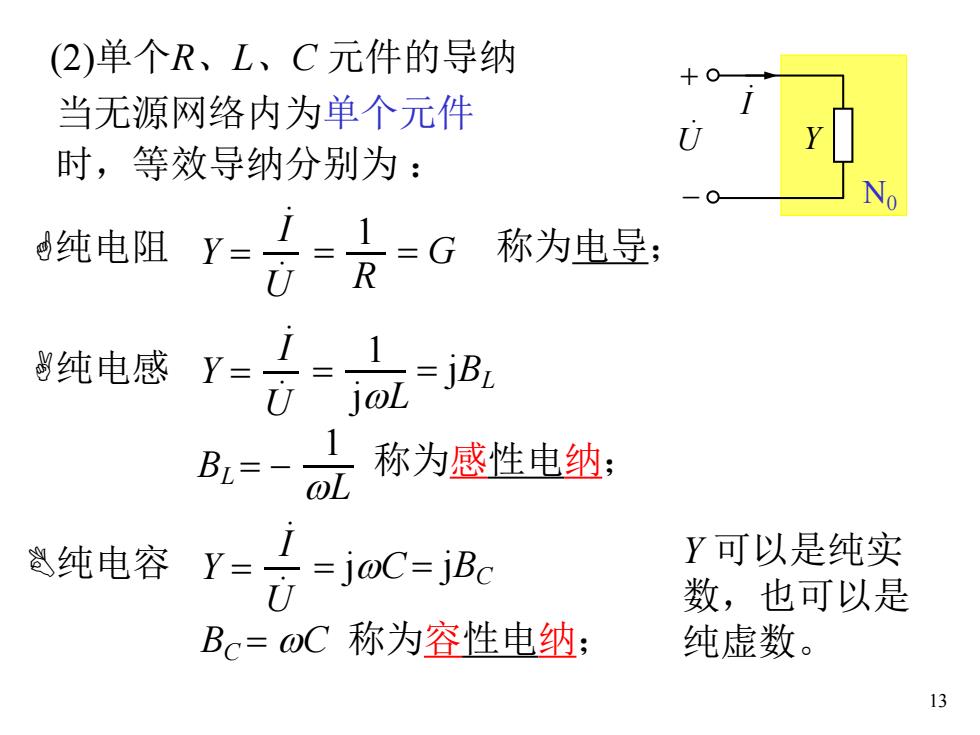
13 (2)单个R、L、C 元件的导纳 称为感性电纳; Y + - . U .I N0 当无源网络内为单个元件 时,等效导纳分别为 : Y = .U .I 纯电阻 = R 1 = G 纯电感 Y = .U .I = jwL 1 = jBL BL = - wL 1 纯电容 Y = .U .I = jwC= jBC BC = wC 称为容性电纳; Y 可以是纯实 数,也可以是 纯虚数。 称为电导;
(3)RLC并联电路 根据VCR和KCL的 相量形式可得: 10 ]0C i-GU -G-j+j0CU-IG+j(B+BoU =(G+jB)U=YU Y= ⊥=G+jB=IYI B B=BL+Bc =-1 Py +0C G B Y=G2+B2 Py=arctg G 导纳三角形 14
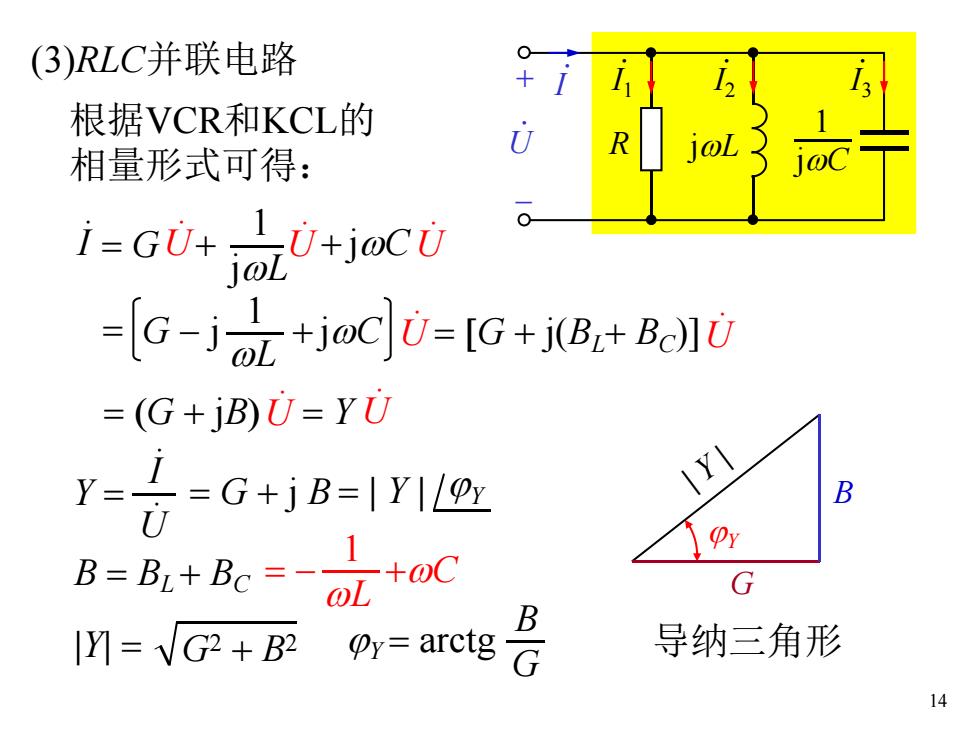
14 (3)RLC并联电路 .I3 jwL jwC 1 .I2 .I1 R .U + - .I 根据VCR和KCL的 相量形式可得: .I = G .U .U jwL 1 + + jwC .U = - wL 1 Y = .U .I = G + j B = | Y | jY B = BL + BC jY = arctg G B +wC |Y| = G2 + B2 jY | Y | G B 导纳三角形 .U .U = Y .U = wL 1 + jwC .U = [G + j(BL+ BC)] = (G + jB) G - j

Y- 1 =G+jB=YLOx U -+0C joL joC y=G2+B2 Py=arctg G 以电压为参考相量相量图 结论:对于RLC并联电路 ①B<0或py<0,称Y为感性; ②B>0或pr>0,称Y为容性; Ic+IL ③B=0或py=0,Y为纯电阻性; U ④G=0,B<0,Y为纯电感性; IR ⑤G=O,B>0,Y为纯电容性。 立电流三角形 15
15 结论: 对于 RLC 并联电路 ① B<0或jY<0,称Y为感性; ② B>0或jY>0,称Y为容性; ③ B=0或jY =0,Y为纯电阻性; ④ G=0,B<0,Y为纯电感性; ⑤ G=0,B>0,Y为纯电容性。 G .I3 jwL jwC 1 .I2 .I1 R .U + - . Y = I .U .I = G + jB = | Y | jY jY = arctg B |Y| = G2+B2 = - wL 1 B = BL+ BC +wC 以电压为参考相量相量图 . . U I . R IL .IC .I jY .IC + .IL 电流三角形