2RC电路的零状态响应 开始S打开,电容C没有被充电。 .uc(0.)=0 在仁0时,将S合上,电路进入 暂态,电源U通过电阻R对电容C 开始充电。 根据KVL→U=uR+uc=RC duc +uc dt 这是一个关于uc的一阶常系数线性非齐次微分方程
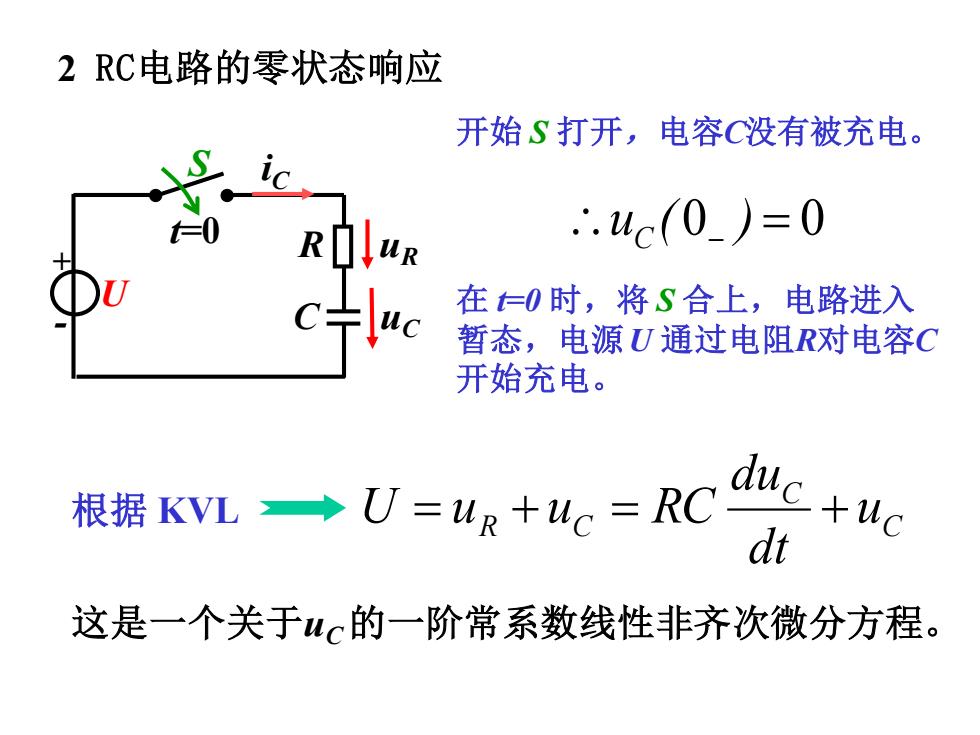
2 RC电路的零状态响应 开始 S 打开,电容C没有被充电。 0 = 0 − u ( ) C 在 t=0 时,将 S 合上,电路进入 暂态,电源U 通过电阻R对电容C 开始充电。 根据 KVL C C R C u dt du U = u + u = RC + 这是一个关于uC 的一阶常系数线性非齐次微分方程。 U + - S R t=0 C uR uC iC

求解微分方程 duc+uc =U RC dt 令通解为hc=4(+u吧 uC是特解,与已知函数U有相同的形式,可令 (=K dK 代入微分方程得 RC +K=U dt ∴K=U→(=U
代入微分方程得 uC 是特解,与已知函数U 有相同的形式,可令 uC = K K U dt dK RC + = K =U uC =U 令通解为 uC uC uC = + u U dt du RC C C 求解微分方程 + =

求解微分方程 duc +uc =U RC dt 令通解为uc=uC+uC u?是补函数,是对应齐次微分方程的通解,令 uc Aem 代入齐次微分方程得特征方程为RCp+1=0 其根为p=-RC .uc Ae Ync Ae h
uC 是补函数,是对应齐次微分方程的通解,令 pt uC = Ae 代入齐次微分方程得特征方程为 RCp +1= 0 RC 其根为 p = − 1 t RC t uC Ae Ae − − = = 令通解为 uC uC uC = + u U dt du RC C C 求解微分方程 + =

求解微分方程 ducuc=U RC dt 令通解为uc=%+4C 所求通解为4c=(+C=U+Ae分 t=0时 4c(0,)=4c0)=0 .A=-U uc =U-Ue =U(1-e%)
所求通解为 t uC uC uC U Ae− = + = + 令通解为 uC uC uC = + u U dt du RC C C 求解微分方程 + = t =0 时 0 = 0 = 0 + − u ( ) u ( ) C C A= −U u U Ue U( e ) t t C − − = − = 1−