电容元件上电压uc不能跃变;电感元件上电流i不能 跃变,也可从另一角度解释: 换路瞬间,若uc发生跃变 i= duc→oo dt 根据KVL:E=迟+uc E为有限值,上式不成立, 所以uc不能发生跃变
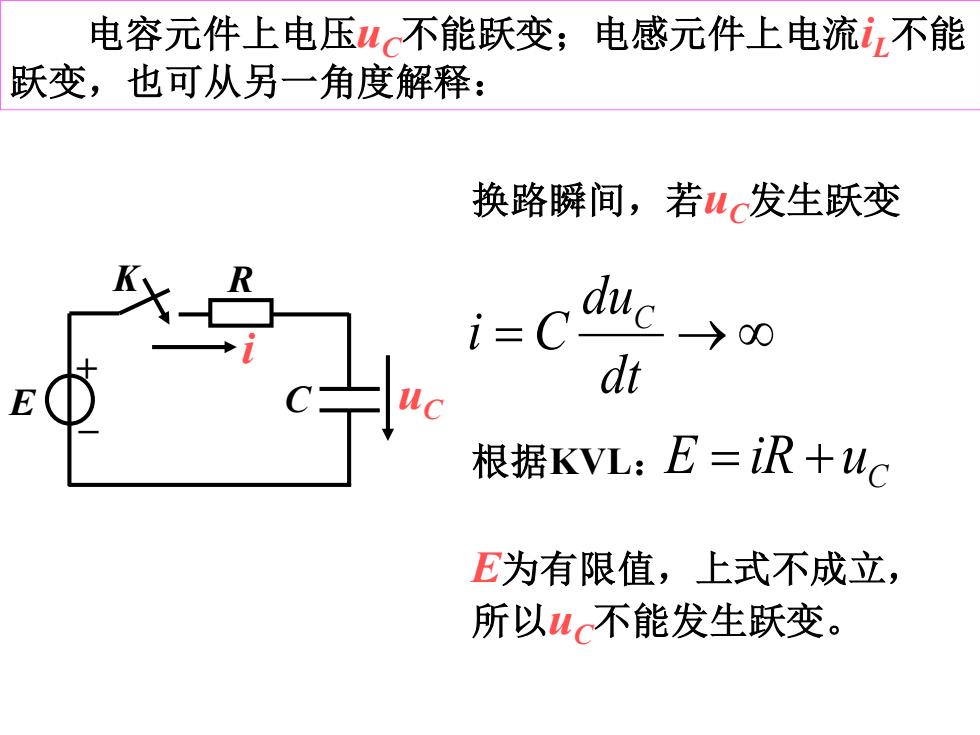
电容元件上电压uC不能跃变;电感元件上电流iL不能 跃变,也可从另一角度解释: E K R + _ C uC i 换路瞬间,若uC发生跃变 = → dt du i C C C E = iR +u E为有限值,上式不成立, 所以uC不能发生跃变。 根据KVL:
换路瞬间,若,发生跃变 u= diL→o0 dt 根据KVL:E=iR+u E为有限值,上式不成立, 所以i不能发生跃变
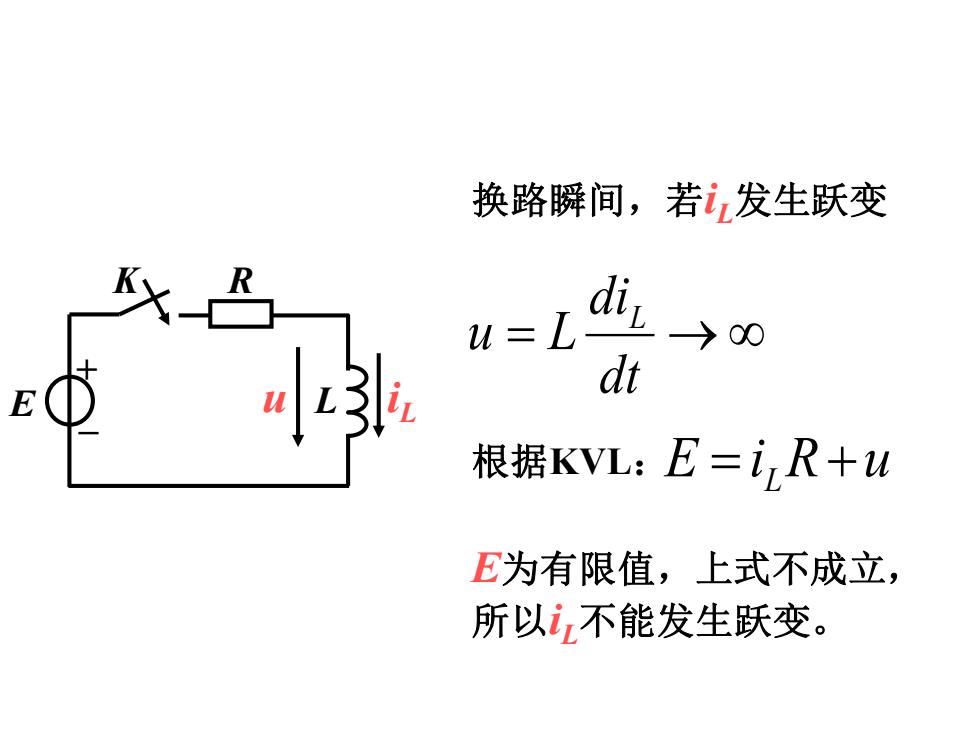
E K R + _ i u L L = → dt di u L L 换路瞬间,若iL发生跃变 根据KVL: E i R u = L + E为有限值,上式不成立, 所以iL不能发生跃变

在换路瞬间,电容元件上电压不能跃变;电感 元件中电流不能跃变,统称为换路定则。 设0表示换路瞬间; 0表示换路前的终了瞬间; 仁0,表示换路后的初始瞬间。 0和0,在数值上都等于0,但前者是1从负值趋 近于0,后者是1从正值趋近于0。 换路定则可以表示为: uc(0.)=uc(0+) iz(0)=iz(0+)
设t=0表示换路瞬间; 换路定则可以表示为: 在换路瞬间,电容元件上电压不能跃变;电感 元件中电流不能跃变,统称为换路定则。 t=0-表示换路前的终了瞬间; t=0+表示换路后的初始瞬间。 0-和0+在数值上都等于0,但前者是t 从负值趋 近于0,后者是t 从正值趋近于0。 u ( ) u ( ) C 0− = C 0+ i ( ) i ( ) L 0− = L 0+
§3RC电路的响应 1RC电路的零输入响应 开始S在位置2,电路已达稳态 .uc(0)=U R 在0时,将S从位置2合到位置1, 电路进入暂态,电容C通过电阻开 始放电。 根据KVL◆ uR+uc RC duc+uc =0 dt 这是一个关于uc的一阶常系数线性齐次微分方程
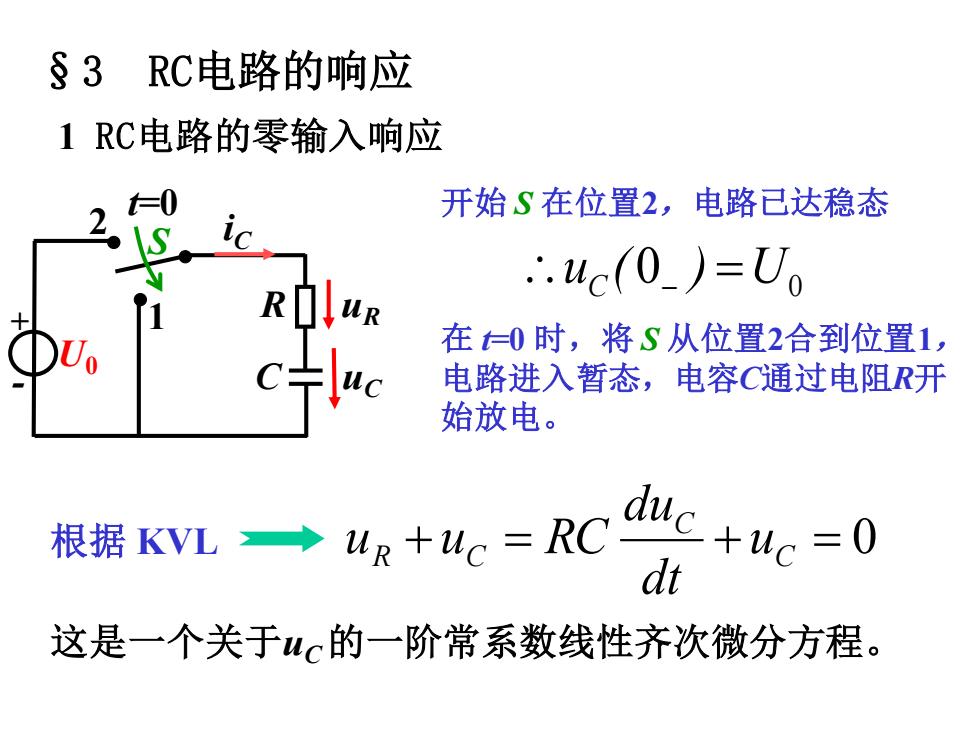
§3 RC电路的响应 1 RC电路的零输入响应 开始 S 在位置2,电路已达稳态 0 uC ( 0− ) =U 在 t=0 时,将 S 从位置2合到位置1, 电路进入暂态,电容C通过电阻R开 始放电。 根据 KVL + = + = 0 C C R C u dt du u u RC 这是一个关于uC 的一阶常系数线性齐次微分方程。 R C uR uC iC 2 U0 + - S 1 t=0

求解微分方程 RC ducuc =0 dt 令通解为uc=AePr 代入微分方程得特征方程为RCp+1=0 其根为p=-RC .uc Ae t=0时uc(0,)=uc(0)=Uo A=U,→4e=Uec
令通解为 pt uC = Ae 代入微分方程得特征方程为 RCp +1= 0 RC 其根为 p = − 1 + = 0 C C u dt du RCRC t uC Ae− = t =0 时 0 uC ( 0+ ) = uC ( 0− ) =U A =U0 求解微分方程 RC t C u U e − = 0