
极限求极限的方法、基本初等函数的导数基本公式、四则运算法则以及复合函数的求导方法、洛 必达法则求00、“0”、0x0”、“0-0”、“10”、00”和0"型未定式的极限方法、不定积分第 一换元法、第二换元法。 三、教学内容 第一章函数与极限 1.基本内容: 函数概念、函数的性质,复合函数:极限,左右极限,无穷小量,无穷大量,极限的四则运 算,两个极限存在准则,两个重要极限:连续性,连续函数的运算性质,基本初等函数和闭区间 上连续函数的性质(最大值,最小值定理和介值定理)。 2.教学基本要求: 理解函数的概念,函数在一点连续的概念:熟悉基本初等函数的性质及其图形;了解反函数、 复合函数概念,极限的cN,-δ定义(对于给出ε求N或8不作过高要求),并能在学习过程中逐 步加深对极限思想的理解,两个极限存在准则,无穷小、无穷大概念,初等函数的连续性:掌握 极限四则运算法则及无穷小的比较:知道在闭间区上连续函数的性质:会用两个重要极限求极限 会判断间断点的类型,能列出简单实际问题中的函数关系。 3.教学重点难点: 函数的概念、极限的&N,8-6定义:连续函数的性质:两个重要极限求极限,判断间断点的 类型,列出简单实际问题中的函数关系:难点为函数极限的-N,-6定义。 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第二章导数与微分 1基本内容 导数概念,导数的几何意义,可导性与连续性之间的关系,导数的运算法则(四则运算、复 合运算、求反函数导数法则),基本初等函数的导数公式,高阶导数,隐函数的导数,对数求导法, 由参数方程所确定的函数的导数,微分概念及其运算法则(包括一阶微分形式不变性),微分在近 似计算及误差估计中的应用。高阶导数的概念,高阶导数的运算法则,参数方程及隐函数的高阶 导数,高阶微分 2.教学基本要求: 理解导数和微分概念熟悉导数和微分的运算法则(包括一阶微分形式不变性)和导数的基 本公式,熟练地求初等函数的一阶,二阶导数:了解导数的几何意义,函数的可导性与连续性的 2
2 极限求极限的方法、基本初等函数的导数基本公式、四则运算法则以及复合函数的求导方法、洛 必达法则求―0/0‖、―∞/ ∞‖、―0×∞‖、―∞-∞‖、―1∞‖、―00‖和―∞0‖型未定式的极限方法、不定积分第 一换元法、第二换元法。 三、教学内容 第一章 函数与极限 1.基本内容: 函数概念、函数的性质,复合函数;极限,左右极限,无穷小量,无穷大量,极限的四则运 算,两个极限存在准则,两个重要极限;连续性,连续函数的运算性质,基本初等函数和闭区间 上连续函数的性质(最大值,最小值定理和介值定理)。 2.教学基本要求: 理解函数的概念,函数在一点连续的概念;熟悉基本初等函数的性质及其图形;了解反函数、 复合函数概念,极限的 ε-N,ε-δ 定义(对于给出 ε 求 N 或 δ 不作过高要求),并能在学习过程中逐 步加深对极限思想的理解,两个极限存在准则,无穷小、无穷大概念,初等函数的连续性;掌握 极限四则运算法则及无穷小的比较;知道在闭间区上连续函数的性质;会用两个重要极限求极限, 会判断间断点的类型,能列出简单实际问题中的函数关系。 3.教学重点难点: 函数的概念、极限的 ε-N,ε-δ 定义;连续函数的性质;两个重要极限求极限,判断间断点的 类型,列出简单实际问题中的函数关系;难点为函数极限的 ε-N,ε-δ 定义。 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第二章 导数与微分 1.基本内容: 导数概念,导数的几何意义,可导性与连续性之间的关系,导数的运算法则(四则运算、复 合运算、求反函数导数法则),基本初等函数的导数公式,高阶导数,隐函数的导数,对数求导法, 由参数方程所确定的函数的导数,微分概念及其运算法则(包括一阶微分形式不变性),微分在近 似计算及误差估计中的应用。高阶导数的概念,高阶导数的运算法则,参数方程及隐函数的高阶 导数,高阶微分。 2.教学基本要求: 理解导数和微分概念;熟悉导数和微分的运算法则(包括一阶微分形式不变性)和导数的基 本公式,熟练地求初等函数的一阶,二阶导数;了解导数的几何意义,函数的可导性与连续性的

关系,高阶导数概念:掌握隐函数和参数式所确定的函数的一阶、二阶导数的求法。 3教学重点难点: 理解导数和微分概念,函数的可导性与连续性的关系:高阶导数的概念,高阶导数的运算法 则,参数方程及隐函数的高阶导数,高阶微分。高阶导数概念,导数的几何意义:难点为高阶导 数,高阶微分的求解。 4教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第三章微分中值定理与导数的应用 1.基本内容: 罗尔定理,格朗日定理,柯西定理,带有拉格朗日余项的奏勒公式。导数的应用,罗必达法 则,函数增减性判定法,函数的极值及其求法,最大值,最小值问题,函数图形的凹凸及其判定 法,拐点及其求法,水平与垂直渐连线,函数图形的描绘,弧微分,求方程近似解的二分法和切 线法。 2.教学基本要求: 理解罗尔定理,拉格朗日定理,函数的极值概念:熟悉柯西定理、泰勒定理:掌握求函数的极 值,判断函数的增减性与函数图形的凹凸性,求函数图形的拐点的方法:求方程近似解的二分法 和切线法:能用导数描述一些经济学中的问题,会应用拉格朗日定理,能描绘函数的图形,会解 简单的最大值和最小值问题。 3.教学重点难点: 掌握函数的极值的计算方法,判断函数的增减性与函数图形的凹凸性,求函数图形的拐点的 方法。熟悉函数图形的描绘。难点为柯西定理、泰勒定理:函数作图。 4教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第四章不定积分 1基本内容: 不定积分的概念,性质,基本积分公式,换元积分法,分部积分法,有理函数、三角函数, 有理函数及简单的无理函数的积分举例。 2.教学基本要求: 理解不定积分的概念和性质,掌握基本积分公式,换元积分法,分部积分法:了解有理函数 的积分,可化为有理函数的积分。 3教学重点难点:
3 关系,高阶导数概念;掌握隐函数和参数式所确定的函数的一阶、二阶导数的求法。 3.教学重点难点: 理解导数和微分概念,函数的可导性与连续性的关系;高阶导数的概念,高阶导数的运算法 则,参数方程及隐函数的高阶导数,高阶微分。高阶导数概念,导数的几何意义;难点为高阶导 数,高阶微分的求解。 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第三章 微分中值定理与导数的应用 1.基本内容: 罗尔定理,格朗日定理,柯西定理,带有拉格朗日余项的泰勒公式。导数的应用,罗必达法 则,函数增减性判定法,函数的极值及其求法,最大值,最小值问题,函数图形的凹凸及其判定 法,拐点及其求法,水平与垂直渐连线,函数图形的描绘,弧微分,求方程近似解的二分法和切 线法。 2.教学基本要求: 理解罗尔定理,拉格朗日定理,函数的极值概念;熟悉柯西定理、泰勒定理;掌握求函数的极 值,判断函数的增减性与函数图形的凹凸性,求函数图形的拐点的方法;求方程近似解的二分法 和切线法;能用导数描述一些经济学中的问题,会应用拉格朗日定理,能描绘函数的图形,会解 简单的最大值和最小值问题。 3.教学重点难点: 掌握函数的极值的计算方法,判断函数的增减性与函数图形的凹凸性,求函数图形的拐点的 方法。熟悉函数图形的描绘。难点为柯西定理、泰勒定理;函数作图。 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第四章 不定积分 1.基本内容: 不定积分的概念,性质,基本积分公式,换元积分法,分部积分法,有理函数、三角函数, 有理函数及简单的无理函数的积分举例。 2.教学基本要求: 理解不定积分的概念和性质,掌握基本积分公式,换元积分法,分部积分法;了解有理函数 的积分,可化为有理函数的积分。 3.教学重点难点:
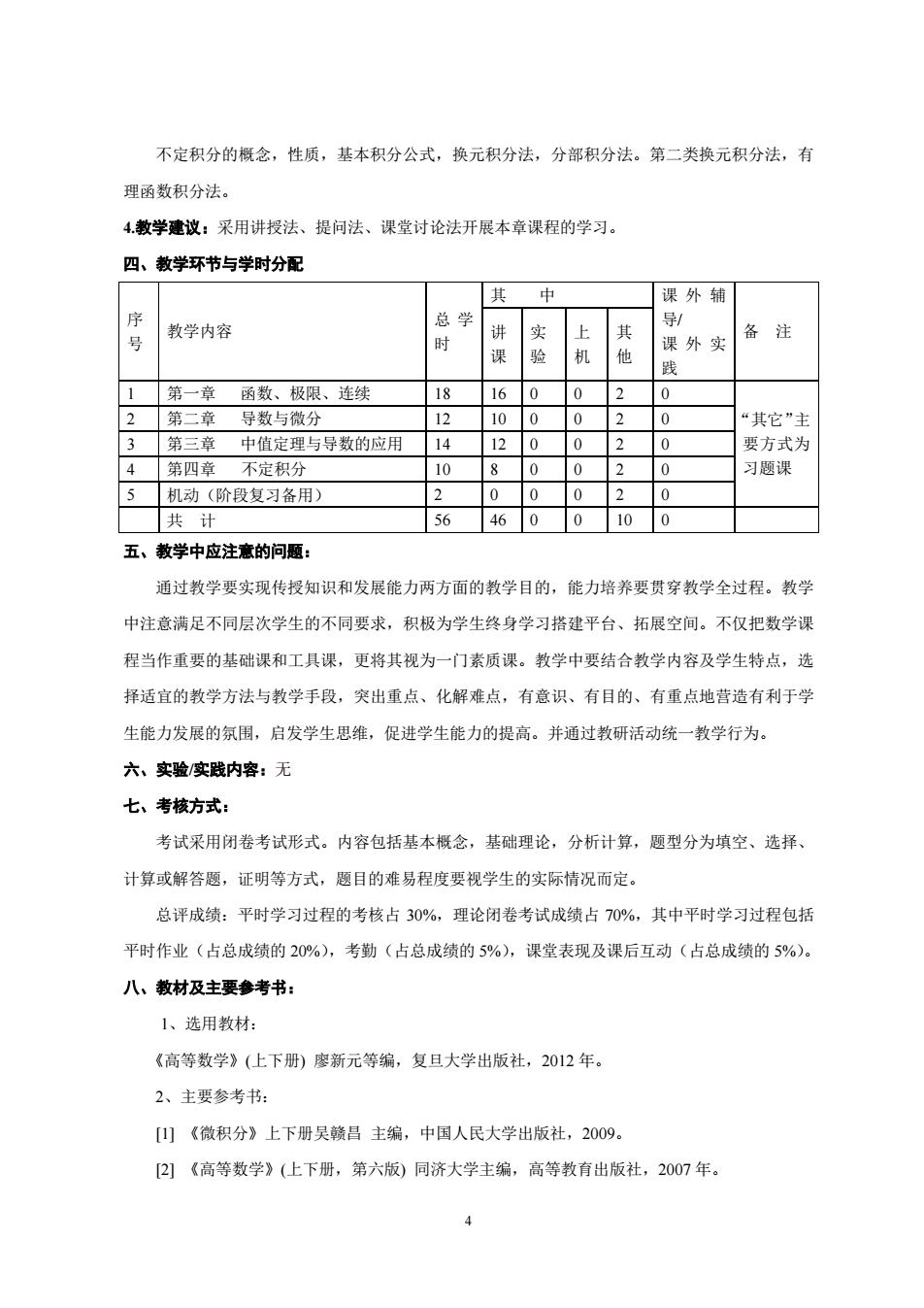
不定积分的概念,性质,基本积分公式,换元积分法,分部积分法。第二类换元积分法,有 理函数积分法。 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习 四、教学环节与学时分配 其 课外辅 教学内容 总学 音 函数、极限、连续 18 160 第二草导数与微分 12 100 其它” 第三章中值定理与导数的应用 14 120 0 0 要方式为 ,第四章不定积分 10 0 习题课 机动(阶段复习备用) 0 共计 56 460 0 100 五、教学中应注意的问题: 通过教学要实现传授知识和发展能力两方面的教学目的,能力培养要贯穿教学全过程。教学 中注意满足不同层次学生的不同要求,积极为学生终身学习搭建平台、拓展空间。不仅把数学课 程当作重要的基础课和工具课,更将其视为一门素质课。教学中要结合教学内容及学生特点,选 择适宜的教学方法与教学手段,突出重点、化解难点,有意识、有目的、有重点地营造有利于学 生能力发展的氛围,启发学生思维,促进学生能力的提高。并通过教研活动统一教学行为。 六、实验实践内容:无 七、考核方式 考试采用闭卷考试形式。内容包括基本概念,基础理论,分析计算,题型分为填空、选择、 计算或解答题,证明等方式,题目的难易程度要视学生的实际情况而定。 总评成绩:平时学习过程的考核占30%,理论闭卷考试成绩占70%,其中平时学习过程包括 平时作业(占总成绩的20%),考勤(占总成绩的5%),课常表现及课后互动(占总成绩的5%)。 八、教材及主要参考书: 1、选用教材: 《高等数学》(上下册)廖新元等编,复旦大学出版社,2012年 2、主要参考书: [山《微积分》上下册吴赣吕主编,中国人民大学出版社,2009。 2《高等数学》(上下册,第六版)同济大学主编,高等教育出版社,2007年。 4
4 不定积分的概念,性质,基本积分公式,换元积分法,分部积分法。第二类换元积分法,有 理函数积分法。 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 四、教学环节与学时分配 序 号 教学内容 总 学 时 其 中 课 外 辅 导/ 课 外 实 践 讲 备 注 课 实 验 上 机 其 他 1 第一章 函数、极限、连续 18 16 0 0 2 0 “其它”主 要方式为 习题课 2 第二章 导数与微分 12 10 0 0 2 0 3 第三章 中值定理与导数的应用 14 12 0 0 2 0 4 第四章 不定积分 10 8 0 0 2 0 5 机动(阶段复习备用) 2 0 0 0 2 0 共 计 56 46 0 0 10 0 五、教学中应注意的问题: 通过教学要实现传授知识和发展能力两方面的教学目的,能力培养要贯穿教学全过程。教学 中注意满足不同层次学生的不同要求,积极为学生终身学习搭建平台、拓展空间。不仅把数学课 程当作重要的基础课和工具课,更将其视为一门素质课。教学中要结合教学内容及学生特点,选 择适宜的教学方法与教学手段,突出重点、化解难点,有意识、有目的、有重点地营造有利于学 生能力发展的氛围,启发学生思维,促进学生能力的提高。并通过教研活动统一教学行为。 六、实验/实践内容:无 七、考核方式: 考试采用闭卷考试形式。内容包括基本概念,基础理论,分析计算,题型分为填空、选择、 计算或解答题,证明等方式,题目的难易程度要视学生的实际情况而定。 总评成绩:平时学习过程的考核占 30%,理论闭卷考试成绩占 70%,其中平时学习过程包括 平时作业(占总成绩的 20%),考勤(占总成绩的 5%),课堂表现及课后互动(占总成绩的 5%)。 八、教材及主要参考书: 1、选用教材: 《高等数学》(上下册) 廖新元等编,复旦大学出版社,2012 年。 2、主要参考书: [1] 《微积分》上下册吴赣昌 主编,中国人民大学出版社,2009。 [2] 《高等数学》(上下册,第六版) 同济大学主编,高等教育出版社,2007 年

B)《数学复习指南》,陈文灯等编,世界图书出版社,2010年。 九、教改说明及其他:无 执笔人:刘小佑系室审核人:廖茂新
5 [3]《数学复习指南》,陈文灯等编,世界图书出版社,2010 年。 九、教改说明及其他: 无 执笔人:刘小佑 系室审核人:廖茂新

《高等数学B1》课程考试大纲 课程编号:130704005 总学时数:56学时 学分:3.5学分 一、考试对象 经济管理类专业。 二、考试目的 本课程考试目的是对学生系统获得一元函数微积分的基本知识,基础理论和常用的运算方法, 比较熟练的运算能力、抽象思维能力、逻辑推理能力和效果检验,以便使学生自我发现哪些知识 学得好,哪些还需要更进一步加强,为学习后继课程和进一步扩大数学知识莫定必要的数学基础, 三、考试要求 1.试题覆盖面要广,既要注意覆盖基础知识和基本技能的掌握程度,同时也要考虑有一定的 区分度。 2.试题难度要适中,要考核学生对基础知识和基本技能的掌握程度,避免过难过偏,考试结 果要能反映大多数学生的实际水平。 3.试题要重视对后继课程学习有所帮助。 4.试题要体现应用性,要有一定量的应用题。 四、考试内容与要求 第一章函数与极限20~30分值 1、考试内容:函数概念、函数的几种特性,反函数、复合函数和初等函数。极限、极限概念, 左右极限,无穷小量,无穷大量,极限的四则运算,两个极限存在准则,两个重要极限,无穷小 的比较。连续性、连续性概念,连续函数的运算性质,基本初等函数和初等函数的连续性,闭区 间上连续函数的性质(最大值,最小值定理和介值定理)。 2、考试要求:理解函数的概念,函数在一点连续的概念:熟悉基本初等函数的性质及其图 形:理解复合函数概念,两个极限存在准则,无穷小、无穷大概念,初等函数的连续性:掌握极 限四则运算法则及无穷小的比较:会用两个重要极限求极限,会判断间断点的类型:能应用最大 值,最小值定理和介值定理来解题。 第二章导数与微分25~30分值 6
6 《高等数学 B1》课程考试大纲 课程编号:130704005 总学时数:56 学时 学分:3.5 学分 一、考试对象 经济管理类专业。 二、考试目的 本课程考试目的是对学生系统获得一元函数微积分的基本知识,基础理论和常用的运算方法, 比较熟练的运算能力、抽象思维能力、逻辑推理能力和效果检验,以便使学生自我发现哪些知识 学得好,哪些还需要更进一步加强,为学习后继课程和进一步扩大数学知识奠定必要的数学基础。 三、考试要求 1. 试题覆盖面要广,既要注意覆盖基础知识和基本技能的掌握程度,同时也要考虑有一定的 区分度。 2. 试题难度要适中,要考核学生对基础知识和基本技能的掌握程度,避免过难过偏,考试结 果要能反映大多数学生的实际水平。 3. 试题要重视对后继课程学习有所帮助。 4. 试题要体现应用性,要有一定量的应用题。 四、考试内容与要求 第一章 函数与极限 20~30 分值 1、考试内容:函数概念、函数的几种特性,反函数、复合函数和初等函数。极限、极限概念, 左右极限,无穷小量,无穷大量,极限的四则运算,两个极限存在准则,两个重要极限,无穷小 的比较。连续性、连续性概念,连续函数的运算性质,基本初等函数和初等函数的连续性,闭区 间上连续函数的性质(最大值,最小值定理和介值定理)。 2、考试要求 :理解函数的概念,函数在一点连续的概念;熟悉基本初等函数的性质及其图 形;理解复合函数概念,两个极限存在准则,无穷小、无穷大概念,初等函数的连续性;掌握极 限四则运算法则及无穷小的比较;会用两个重要极限求极限,会判断间断点的类型;能应用最大 值,最小值定理和介值定理来解题。 第二章 导数与微分 25~30 分值