
历些毛子代枝大兽 第三讲:复杂网络结构模型 XIDIAN UNIVERSITY >WS小世界网络模型 现实网络的小世界特性。 现实世界大多数网络尽管规模很大,但是任意两个节(顶)点间却 有一条相当短的路径的事实。以日常语言来说,它反映的是相互连 边的数目可以很少(边密度较低),但平均路径长度却很短。 ·举例:社会网络。 ·小世界网络:是一类网络的统称,这类网络平均路径较短,聚集系 数较高。 7
第三讲:复杂网络结构模型 7 WS小世界网络模型 现实网络的小世界特性。 现实世界大多数网络尽管规模很大,但是任意两个节(顶)点间却 有一条相当短的路径的事实。以日常语言来说,它反映的是相互连 边的数目可以很少(边密度较低),但平均路径长度却很短。 • 举例:社会网络。 • 小世界网络:是一类网络的统称,这类网络平均路径较短,聚集系 数较高

历安毛子代枚大等 第三讲:复杂网络结构模型 XIDIAN UNIVERSITY WS小世界网络模型。 1998年,Watts和Strogatz提出了小世界网络这一概念,并建立 了WS模型。 第一步:从规则图开始,考虑一个含有N个点的最近邻耦合网络,它们 围成一个环,其中每个节点都与它左右相邻的各K/2节点相连,K是偶 数。 第二步:随机化重连,以概率随机地从新连接网络中的每个边,即将 边的一个端点保持不变,而另一个端点取为网络中随机选择的一个节点 。其中规定,任意两个不同的节点之间至多只能有一条边,并且每一个 节点都不能有边与自身相连
• 第一,小世界特性。 大多数网络尽管规模很大,但是任意两个节(顶)点间却有一条 相当短的路径的事实。以日常语言来说,它反映的是相互连边的 数目可以很少(边密度较低),但平均路径长度却很短。 • 举例:环形规则网络, 小世界网络 • 小世界网络:是一类网络的统称,这类网络平均路径较短,聚集 系数较高。 • WS小世界网络模型。 1998年, Watts和Strogatz提出了小世界网络这一概念,并建立 了WS模型。 第一步:从规则图开始,考虑一个含有N个点的最近邻耦合网络,它们 围成一个环,其中每个节点都与它左右相邻的各K/2节点相连,K是偶 数。 第二步:随机化重连,以概率p随机地从新连接网络中的每个边,即将 边的一个端点保持不变,而另一个端点取为网络中随机选择的一个节点 。其中规定,任意两个不同的节点之间至多只能有一条边,并且每一个 节点都不能有边与自身相连。 第三讲:复杂网络结构模型

历些毛子科枚大” 第三讲:复杂网络结构模型 XIDIAN UNIVERSITY WS小世界网络模型。 WS小世界模型可以在重连概率p=0到p=1之间灵活的构建网络。p=0是完全的 规则网络,p=1是完全的随机网络,0<p<1则产生小世界网络。重连概率p取 不同值,所产生网络的平均路径长度和平均聚集系数也不同,它们都可认为 是p的函数,分别表示为L(p)和C(p)。 (ad)规则网络 (b)小世界网络 (c)随机网络 p=( 随机重连 增加随机性 人们最敢兴趣的网络是其具有稀疏连接,但又不至于稀疏得使网络不联通, 为此让W>>K>>inW>>1。K~>inN能保证网络是联通的,N>>K保证网络具有 稀疏性,inN>>1保证网络有一定的规模
• 第一,小世界特性。 大多数网络尽管规模很大,但是任意两个节(顶)点间却有一条 相当短的路径的事实。以日常语言来说,它反映的是相互连边的 数目可以很少(边密度较低),但平均路径长度却很短。 • 举例:环形规则网络, 小世界网络 • 小世界网络:是一类网络的统称,这类网络平均路径较短,聚集 系数较高。 • WS小世界网络模型。 WS小世界模型可以在重连概率p=0到p=1之间灵活的构建网络。p=0是完全的 规则网络,p=1是完全的随机网络,0<p<1则产生小世界网络。重连概率p取 不同值,所产生网络的平均路径长度和平均聚集系数也不同,它们都可认为 是p的函数,分别表示为L(p)和C(p)。 人们最敢兴趣的网络是其具有稀疏连接,但又不至于稀疏得使网络不联通, 为此让N>>K>>linN>>1。K>>linN能保证网络是联通的,N>>K保证网络具有 稀疏性,linN>>1保证网络有一定的规模。 第三讲:复杂网络结构模型 (a) 规则网络 (b) 小世界网络 (c) 随机网络 p=0 增加随机性 随机重连

历安毛子代枚大学 第三讲:复杂网络结构模型 XIDIAN UNIVERSITY NW小世界网络模型。 WS小世界模型的问题在于当网络密度较小(较小)时,边重连可能导致 网络不联通。 NW小世界网络模型。1999年,Newman和Watts提出了另一种比较常用的小 世界模型,称为NW小世界网络模型,其基本步骤如下: 步骤1:产生一个环形的规则近邻连接网络,网络有个节点,每个节点和 近邻的k个节点相连: 步骤2:在任意两个节点之间以概率随机加边。 NW小世界网络模碧V小世网销蒸型的S真步骤2,NW模型是随 (a)规则网络 机重连,边的总 边的总数是增加的。 随机加边 增加随机性
• 第一,小世界特性。 大多数网络尽管规模很大,但是任意两个节(顶)点间却有一条 相当短的路径的事实。以日常语言来说,它反映的是相互连边的 数目可以很少(边密度较低),但平均路径长度却很短。 • 举例:环形规则网络, 小世界网络 • 小世界网络:是一类网络的统称,这类网络平均路径较短,聚集 系数较高。 • NW小世界网络模型。 WS小世界模型的问题在于当网络密度较小(K较小)时,边重连可能导致 网络不联通。 NW小世界网络模型。1999年,Newman和Watts提出了另一种比较常用的小 世界模型,称为NW小世界网络模型,其基本步骤如下: 步骤1:产生一个环形的规则近邻连接网络,网络有N个节点,每个节点和 近邻的k个节点相连; 步骤2:在任意两个节点之间以概率p随机加边。 NW小世界网络模型和WS小世界网络模型的区别在于步骤2,NW模型是随 机重连,边的总数不会增加,而NW模型是随机加边,边的总数是增加的。 第三讲:复杂网络结构模型 (a) 规则网络 (b) 小世界网络 (c) 小世界网络 增加随机性 随机加边
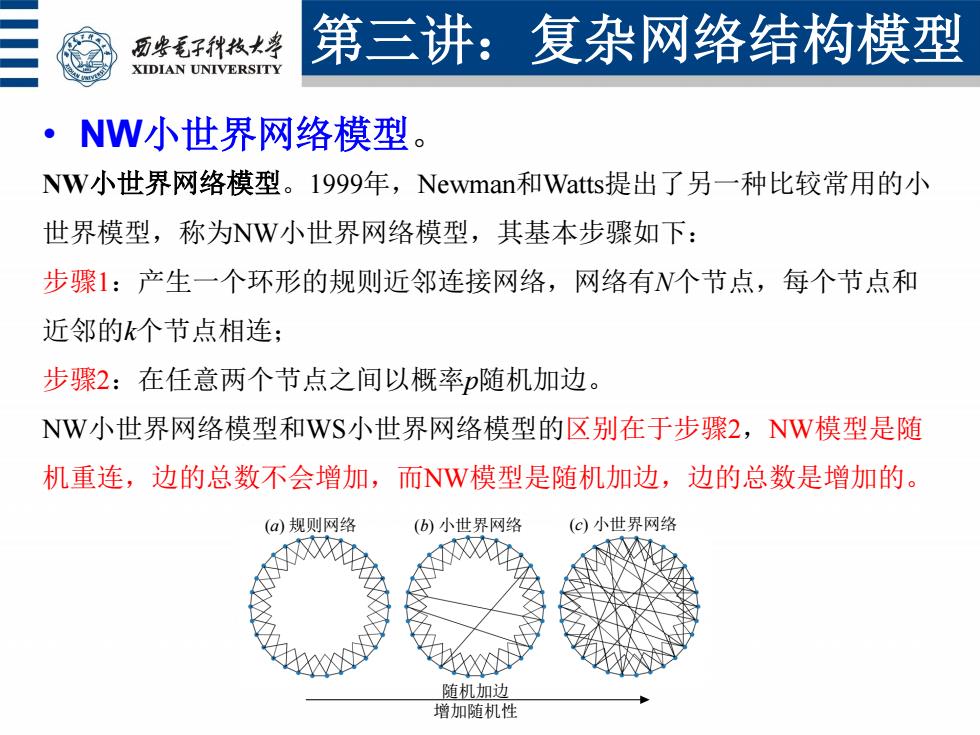
面些毛子种枝大学 第三讲:复杂网络结构模型 XIDIAN UNIVERSITY ·NW小世界网络模型。 NW小世界网络模型。1999年,Newman和Wats提出了另一种比较常用的小 世界模型,称为NW小世界网络模型,其基本步骤如下: 步骤1:产生一个环形的规则近邻连接网络,网络有个节点,每个节点和 近邻的k个节点相连; 步骤2:在任意两个节点之间以概率随机加边。 NW小世界网络模型和WS小世界网络模型的区别在于步骤2,NW模型是随 机重连,边的总数不会增加,而NW模型是随机加边,边的总数是增加的。 (a)规则网络 (b)小世界网络 (c)小世界网络 随机加边 增加随机性
• 第一,小世界特性。 大多数网络尽管规模很大,但是任意两个节(顶)点间却有一条 相当短的路径的事实。以日常语言来说,它反映的是相互连边的 数目可以很少(边密度较低),但平均路径长度却很短。 • 举例:环形规则网络, 小世界网络 • 小世界网络:是一类网络的统称,这类网络平均路径较短,聚集 系数较高。 • NW小世界网络模型。 NW小世界网络模型。1999年,Newman和Watts提出了另一种比较常用的小 世界模型,称为NW小世界网络模型,其基本步骤如下: 步骤1:产生一个环形的规则近邻连接网络,网络有N个节点,每个节点和 近邻的k个节点相连; 步骤2:在任意两个节点之间以概率p随机加边。 NW小世界网络模型和WS小世界网络模型的区别在于步骤2,NW模型是随 机重连,边的总数不会增加,而NW模型是随机加边,边的总数是增加的。 第三讲:复杂网络结构模型 (a) 规则网络 (b) 小世界网络 (c) 小世界网络 增加随机性 随机加边