
博弈的基本分析方法 1上策均衡 2严格下策反复消去法 3划线法 4箭头法
博弈的基本分析方法 1 上策均衡 2 严格下策反复消去法 3 划线法 4 箭头法

1上策均衡 上策:不管其它博弈方选择什么策略,一博弈方的 某个策略给他带来的得益始终高于他的其它的策 略,至少不低于其他策略的策略。 4,(s,S)≥4(⑤,5),对任意的3∈S,s≠, 智猪博弈中的小猪“等待”;囚徒的困境中的 “坦白”;双寡头削价中“低价”。 小猪 按 等 待 D 5-5 按 5,1 4,4 0-10 猪 等待 9,-1 0,0 -10 -1-1
1 上策均衡 上策:不管其它博弈方选择什么策略,一博弈方的 某个策略给他带来的得益始终高于他的其它的策 略,至少不低于其他策略的策略。 对任意的 智猪博弈中的小猪“等待”;囚徒的困境中的 “坦白”;双寡头削价中“低价”。 5, 1 4, 4 9, -1 0, 0 大 猪 按 等 待 小猪 按 等 待 -5 -5 0 -10 -10 0 -1 -1 D D C C ' ( , ) ( , ), i i i i i i u s s u s s ' , i i s S ' , i i s s
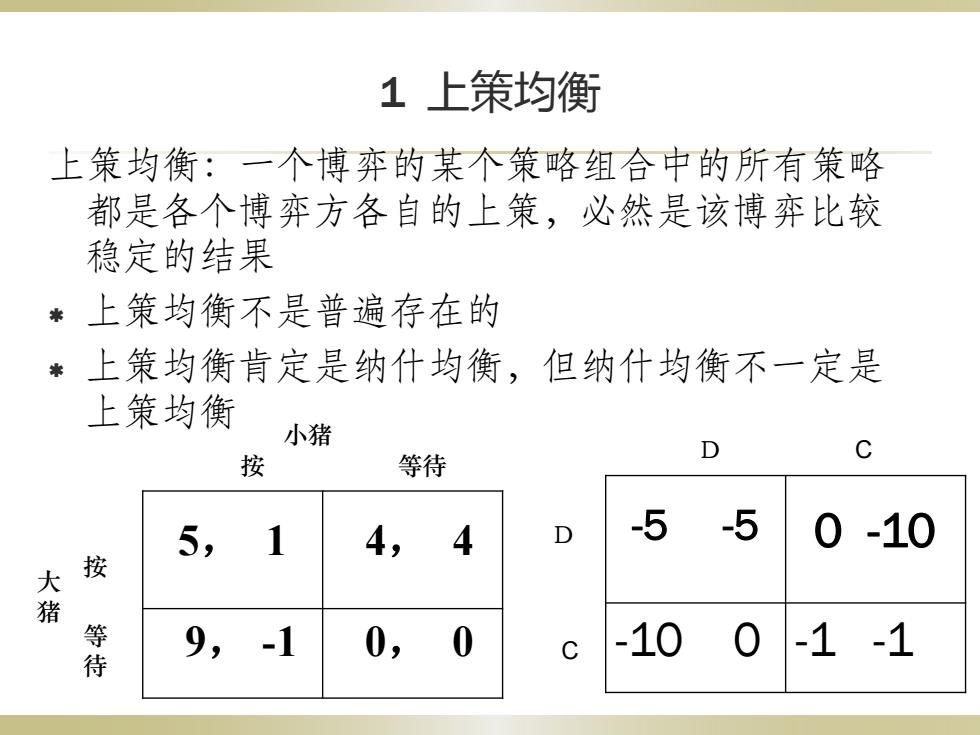
1上策均衡 上策均衡:一个博弈的某个策略组合中的所有策略 都是各个博弈方各自的上策,必然是该博弈比较 稳定的结果 *上策均衡不是普遍存在的 上策均衡肯定是纳什均衡,但纳什均衡不一定是 上策均衡 小猪 按 等待 5,1 4, 4 D -5-5 0-10 大 按 等待 9,-1 0, 0 -100-1-1
1 上策均衡 上策均衡:一个博弈的某个策略组合中的所有策略 都是各个博弈方各自的上策,必然是该博弈比较 稳定的结果 上策均衡不是普遍存在的 上策均衡肯定是纳什均衡,但纳什均衡不一定是 上策均衡 5, 1 4, 4 9, -1 0, 0 大 猪 按 等待 小猪 按 等 待 -5 -5 0 -10 -10 0 -1 -1 D D C C
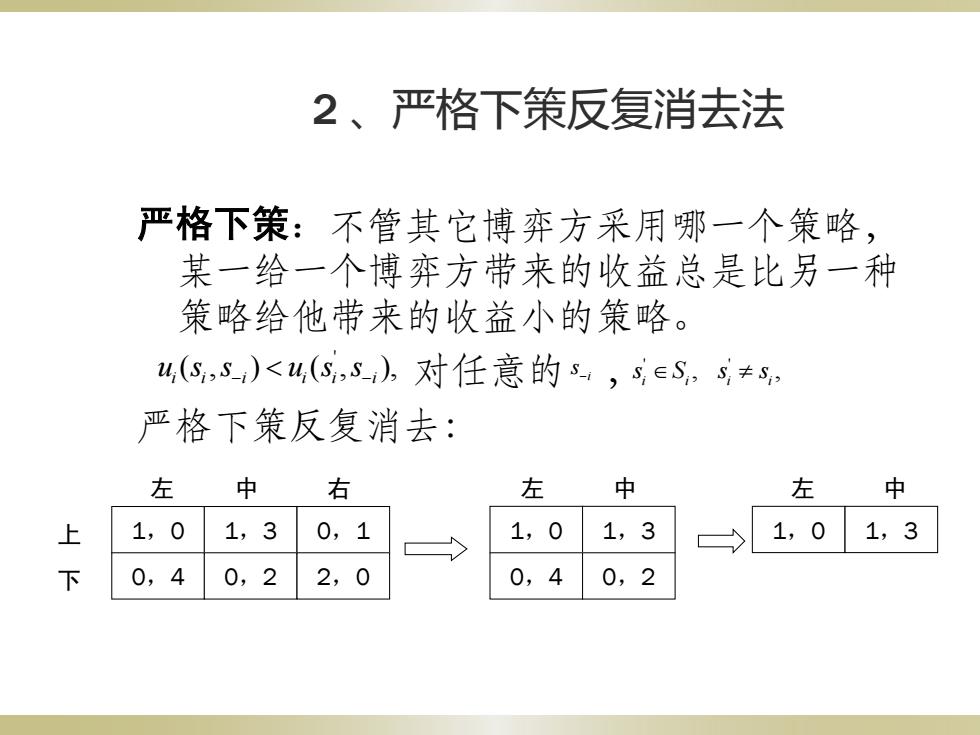
2、严格下策反复消去法 严格下策:不管其它博弈方采用哪一个策略, 某一给一个博弈方带来的收益总是比另一种 策略给他带来的收益小的策略。 4,(s5)<4(S,5,对任意的s,seS,≠s, 严格下策反复消去: 左 中 右 左 中 左 中 上 1,0 1,3 0,1 1,0 1,3 1,0 1,3 下 0,4 0,2 2,0 0,4 0,2
2 、严格下策反复消去法 严格下策:不管其它博弈方采用哪一个策略, 某一给一个博弈方带来的收益总是比另一种 策略给他带来的收益小的策略。 对任意的 , 严格下策反复消去: 1,0 1,3 0,1 0,4 0,2 2,0 左 中 右 上 下 1,0 1,3 0,4 0,2 左 中 1,0 1,3 左 中 ' ( , ) ( , ), i i i i i i u s s u s s ' , i i s S ' , i i si s s

纳什均衡与严格下策反复消去法 命题1:在n个博弈方的博弈G={S1,…Sn4,un}中,如果严格下 策反复消去法排除了除(S,…Sn之外的所有策略组合,那么 (s1,…sn) 一定是该博奔的唯一的纳什均衡 命题2:在n个博弈方的博弈中G={S,…Sm4,…un}中,如果 (s,,)是G的一个纳什均衡,那么严格下策反复消去法一定 不会将它消去 上述两个命题保证在进行纳什均衡分析之前先通过严格下策 反复消去法简化博弈是可行的
纳什均衡与严格下策反复消去法 命题1:在n个博弈方的博弈 中,如果严格下 策反复消去法排除了除 之外的所有策略组合,那么 一定是该博弈的唯一的纳什均衡 命题2:在n个博弈方的博弈中 中,如果 是 的一个纳什均衡,那么严格下策反复消去法一定 不会将它消去 上述两个命题保证在进行纳什均衡分析之前先通过严格下策 反复消去法简化博弈是可行的 ( , ) * * i n s s { , ; , } G S1 Sn u1 un ( , ) * * i n s s ( , ) * * i n s s { , ; , } G S1 Sn u1 un G