
《1)无=4时e0s%=1.则g=0 (2)名=时,04=0则码=±经因。<0取码- 《3)无=10x10w时.o0s%=05则%=号因%<0取码=子 名-10x0时5题=号6a取,- 3 旋转矢量法:分别面出四个不同初始找态的旋转美量图,如图13-7()所示,它们所对应 的初相分测为%-0,%-夏/2,停-g/3,4=4红/3: 丽幅A,角频率四,初相口均确定后。则各相应状志下的运动方程为 41)x=(2.0×10w0os4g (2)xy (3)-20x0mco4ag+ (4)=xm)co 138有一弹簧,当其下端挂一质量为曲的物体时,伸长量为9.8×102m。若使物体上下振动, 且规定向下为正方向.《1)0时,物体在平衡位置上方80×10■处,由静止开始向下运动, 象运动方程。(2)0时。物体在平衡位置并以060m小的速度向上运动,乘运动方程, b 13-8 分析求运动方程。也就是要确定握动的三个特征物理量A、⑧,和?:其中量动的角频率是 山弹簧暴予系统的国有性质(振子质量■及弹簧劲度系数k》浇定的。即心■、√/m,可根据物 体受力平衡时弹簧的伸长来计算:探幅A和初相需要复据初始条件确定。 解物体受力平衡时,弹性力F与重力P的大小相等,即P。而此时弹簧的伸长量 W=98×10广刚。则弹簧的动度系数k=F/山=四/W。系统作简著运动的角频率为 a=1w-g1-10s (1)设系绕平衡时,物体所在处为坐标眼点,向下为夏轴正向。由初始条件10时, 。=8.0x0m,,=0可得耀幅4-√2+(0/了=80x10周:应用旋转矢量法可确定
(1) x0 = A时,cos1 =1,则1 = 0; (2) 时, ,则 ,因 ,取 ; 2 0 2 0 cos 2 0 2 0 2 x = A = = v = (3) 时, ,则 ,因 ,取 ; 3 0 3 1.0 10 cos 3 0.5 3 0 3 2 0 = = = = − x m v (4) 时, ,则 ,因 ,取 ; 3 4 0 3 1.0 10 cos 4 0.5 4 0 4 2 0 = − = − = = − x m v 旋转矢量法:分别画出四个不同初始状态的旋转关量图,如图 13-7(b)所示,它们所对应 的初相分别为 1 = 0,1 = / 2 ,1 = / 3,1 = 4 / 3。 振幅 A、角频率 、初相 均确定后,则各相应状态下的运动方程为 (1) x (2.0 10 m) cos(4 s )t −2 −1 = (2) ] 2 (2.0 10 )cos[(4 ) 2 1 = + − − x m s t (3) ] 3 (2.0 10 )cos[(4 ) 2 1 = + − − x m s t (4) ] 3 4 (2.0 10 ) cos[(4 ) 2 1 = + − − x m s t 13-8 有一弹簧,当其下端挂一质量为 m 的物体时,伸长量为 9.8×10-2m。若使物体上下振动, 且规定向下为正方向。(1)t=0 时,物体在平衡位置上方 8.0×10-2m 处,由静止开始向下运动, 求运动方程。(2)t=0 时,物体在平衡位置并以 0.60m/s 的速度向上运动,求运动方程。 13-8 分析 求运动方程,也就是要确定振动的三个特征物理量 A、 ,和 。 其中振动的角频率是 由弹簧振子系统的固有性质(振子质量 m 及弹簧劲度系数 k)决定的,即 = k /m ,可根据物 体受力平衡时弹簧的伸长来计算;振幅 A 和初相 需要根据初始条件确定。 解 物体受力平衡时,弹性力 F 与重力 P 的大小相等,即 F=mg。 而此时弹簧的伸长量 l m 2 9.8 10− = 。 则弹簧的劲度系数 k = F /l = mg /l 。 系统作简谐运动的角频率为 1 / / 10 − = k m = g l = s (1)设系统平衡时,物体所在处为坐标原点,向下为 x 轴正向。 由初始条件 t=0 时, x m 2 10 8.0 10 − = , v10 = 0 可得振幅 A x v m 2 2 10 10 2 ( / ) 8.0 10− = + == ;应用旋转矢量法可确定
初相级=。[图13-8(a)]。则运动方程为 马,-(80×0m)cosk0:r+r] (2》t0时,x多=0,=0.6m手1,同理可得4=√”+n/=60x103m: %-/2:[图13-8(h)],则运动方程为 无=(6.0×109m0osk10sr+0.5xl 159某银动质点的x-1曲线如图所示,试求:《1)运动方程:(2)点P对应的相位:(3)到达 点P相应位置所需要的时间, 4¥ 0.10 0.05 4.0 13-9 分析由已知运动方程西振诗由线和由振动曲线求运功方程是佩功中常见的两类利题。本题藏 是要通过x1图线确定丽动的三个特征量量人,#,和风,从而写出运动方程。由线最大额值 即为扳幅:而。,通常可通过旋转矢量法或解析法解出,一毅采用鬓转矢量法比校方便 解(1)质点振动振氢A=0.10,而由服功曲线可面出1=0和=48时能转矢量,如图 13-9(b)所示。 由图可见初相风=-好/到暖风=5知/),雨由,-%)上乃+为得 世=5r/24,则运动方程为 x=0.10网e0 票-列 (2)图14-9(a》中点P的位置是质点从A/2处运 动到正向的端点处。应的旋转关量图如图13-10(C) 所示。当初相取风=一/3时,点P的相位为 ,=+例,-0=0(如果初相取%=5好/3,则点P f=0 相应的相位应表示为。=+0,-0)=2灯). (e) (3)由装特关量图可得%。-0)-乃期(,=16 130在一块平板下装有弹簧。平板上故一质景为1处g的重物。现使平板沿经直方向做上下 简话运动,属期为030s,振幅为2.0×10m。求:《1)平板到最低点时,重物对平板的作用力: (2)若顿率不变。则平板以多大的据幅据时时,重物金跳离平板:(3)若探解不变,则平版以 多大的顿率振动时,重物会洗离平板?
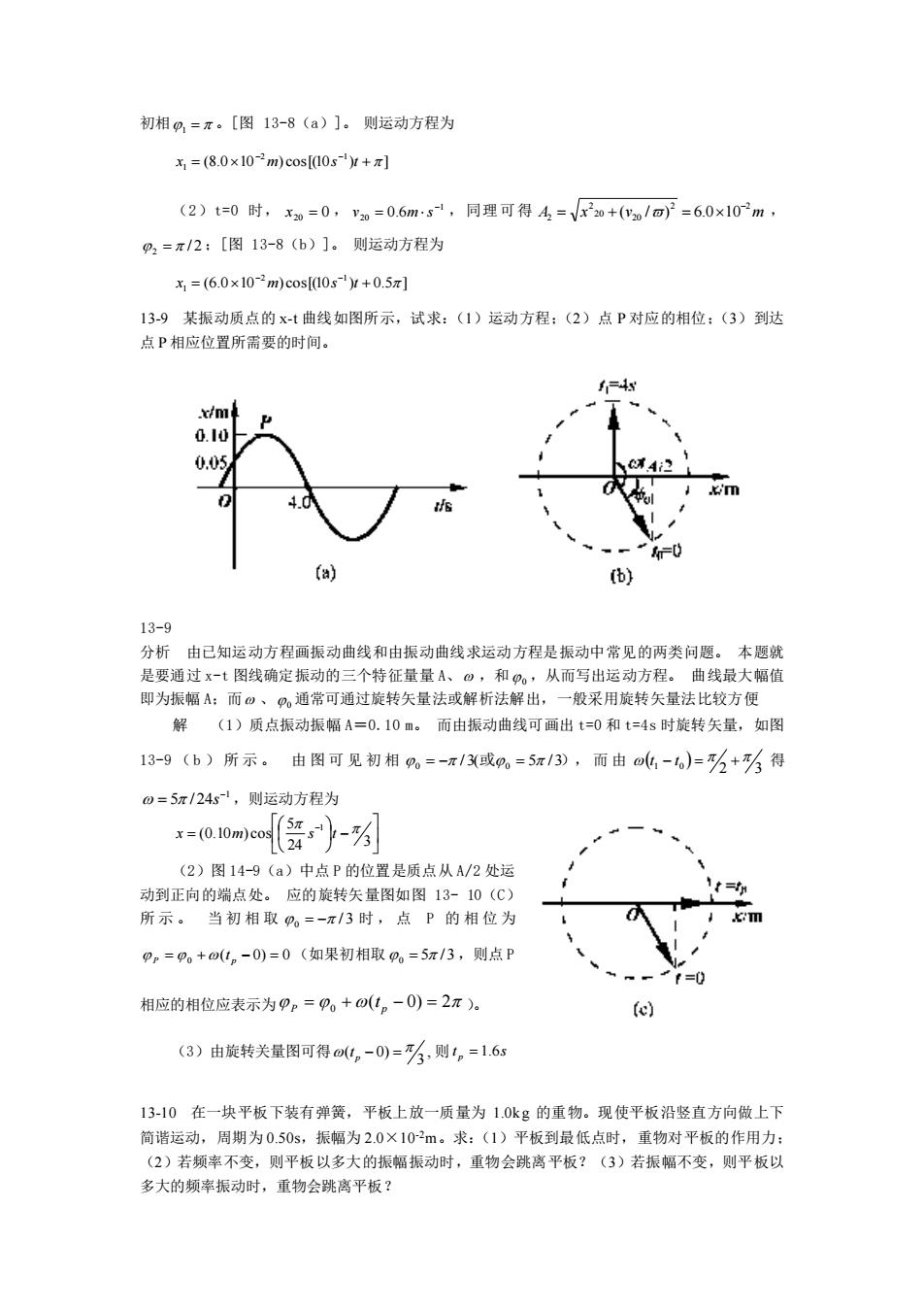
初相 1 = 。[图 13-8(a)]。 则运动方程为 (8.0 10 ) cos[(10 ) ] 2 1 1 = + − − x m s t (2)t=0 时, x20 = 0 , 1 20 0.6 − v = m s ,同理可得 A x v m 2 2 20 20 2 2 ( / ) 6.0 10− = + = , 2 = / 2 ;[图 13-8(b)]。 则运动方程为 (6.0 10 ) cos[(10 ) 0.5 ] 2 1 1 = + − − x m s t 13-9 某振动质点的 x-t 曲线如图所示,试求:(1)运动方程;(2)点 P 对应的相位;(3)到达 点 P 相应位置所需要的时间。 13-9 分析 由已知运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题。 本题就 是要通过 x-t 图线确定振动的三个特征量量 A、 ,和 0 ,从而写出运动方程。 曲线最大幅值 即为振幅 A;而 、 0 通常可通过旋转矢量法或解析法解出,一般采用旋转矢量法比较方便 解 (1)质点振动振幅 A=0.10 m。 而由振动曲线可画出 t=0 和 t=4s 时旋转矢量,如图 13-9 (b )所示。 由图可见初相 0 = − / 3(或 0 = 5 / 3) ,而由 ( ) 2 3 1 0 t − t = + 得 1 5 / 24 − = s ,则运动方程为 − = − 3 24 5 (0.10 ) cos 1 x m s t (2)图 14-9(a)中点 P 的位置是质点从 A/2 处运 动到正向的端点处。 应的旋转矢量图如图 13- 10(C) 所示。 当初相取 0 = − / 3 时,点 P 的相位为 P = 0 +(t p − 0) = 0 (如果初相取 0 = 5 /3 ,则点 P 相应的相位应表示为 P = 0 +(t p − 0) = 2 )。 (3)由旋转关量图可得 , 3 ( − 0) = p t 则 t s p = 1.6 13-10 在一块平板下装有弹簧,平板上放一质量为 1.0kg 的重物。现使平板沿竖直方向做上下 简谐运动,周期为 0.50s,振幅为 2.0×10-2m。求:(1)平板到最低点时,重物对平板的作用力; (2)若频率不变,则平板以多大的振幅振动时,重物会跳离平板?(3)若振幅不变,则平板以 多大的频率振动时,重物会跳离平板?