《电工技术》课程教学课件（课件讲稿）第4章 正弦交流电路

·【例】把复数A=6+8化为三角函数式、指数式和 极坐标式。 解：r=Va2+b2=V62+82=10 0=arctan =53 a 三角函数式：A=10(cos53°+jsin53) 指数式： A=10e53° 极坐标式： A=10∠53° 09:41 21

09:41 21 • 【例】把复数A=6+j8化为三角函数式、指数式和 极坐标式。 6 8 10 2 2 2 2 r  a  b     arctan  53 a b  三角函数式： 解： A 10cos53 jsin53   53 10 j A e A 1053 指数式： 极坐标式：

·1、A=3+4,A2=2+j,求A=A,+A2,并化成极坐 标式。 A=A,+A2=(3+4)+(2+) =(3+2)+(4+1)=5+j5=52∠45° 2、A=6+j8,A2=4-j3,求A=A/A2并化成代数式。 A=4=6+8 10∠53° A24-j35∠-37° =2∠90°=j2 (6+j8):(4+j3)-j50 =j2 (4-3)(4+3) 25 09:41 22

09:41 22 (3 4) (2 ) 1 2 A  A  A   j   j • 1、A1 =3+j4,A2 =2+j，求 A=A1+A2 ，并化成极坐 标式。  5 245    -     2 90 5 37 10 53  (3 2)  j(4 1)  5 j5 2、A1 =6+j8，A2 =4-j3，求 A=A1 /A2并化成代数式。 4 3 6 8 2 1 j j A A A -     j2 25 j50  (4 3) (4 3) (6 8) (4 3) j j j j -        j2

旋转因子ed=1∠0是一个模等于1，辐角 ti 为0的复数。 Aej0 任意一个复数A=4Aei乘以e,等于把A 逆时针旋转0角度，而模4保持不变。 e90=cos90°+jsin90°=j +1 0 .j=V-1=e9w=1∠90 .ew=cos(-90)+jsin(-90)=-j -j=1=e=1∠-90 e18w=cos180°+jsin180°=-1 09:41 -1=2=e1s0°=1∠180 23

09:41 23  旋转因子 e j =1∠是一个模等于1，辐角 为的复数。  任意一个复数A=|A|e jα乘以e j ，等于把A 逆时针旋转 角度，而模|A|保持不变。 +j o +1 A a Ae j  e cos90 jsin90 j j9 0        j 1 e 1 90 j9 0     -    e cos( ) jsin( ) j j  -  -  - -     90 90 90   e 1 90 1 j j9 0  -    - - j e cos180 jsin180 1 j180    -     1 j e 1 180 2 j180    -    

4.2.2正弦量用旋转有向线段表示 设正弦量：i=Isin(ot+y) @t 若：有向线段长度= 有向线段与横轴夹角=初相位少 有向线段以速度ω按逆时针方向旋转 则：该旋转有向线段每一瞬时在纵轴上的投影即 表示相应时刻正弦量的瞬时值。 09:41 24

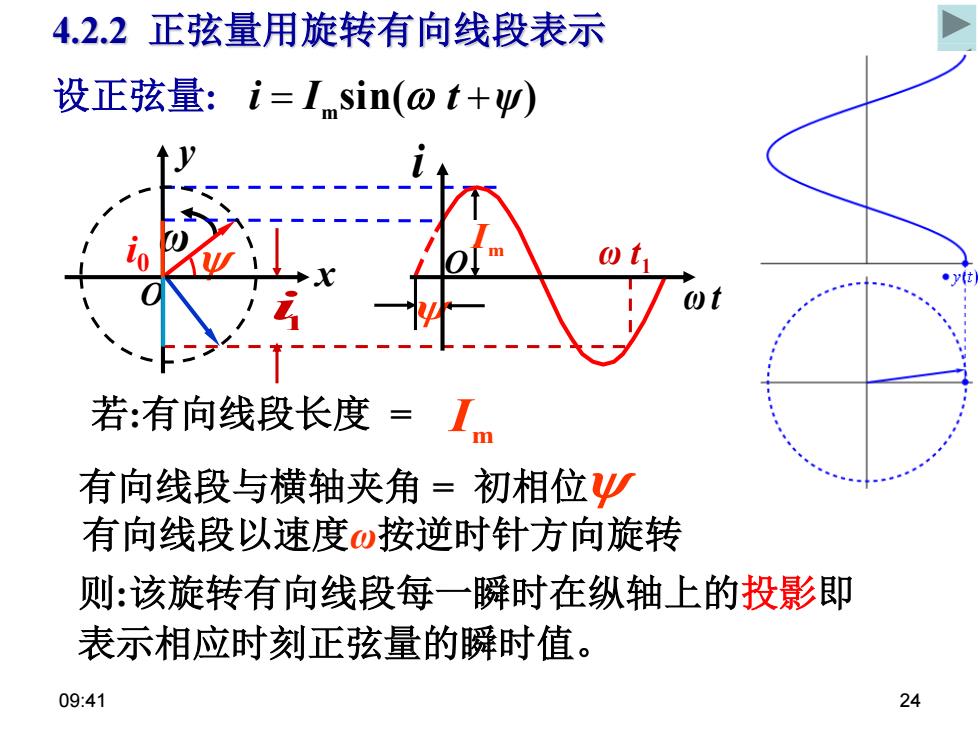
09:41 24 4.2.2 正弦量用旋转有向线段表示 ω sin( ) 设正弦量: i  I m  t ψ 若:有向线段长度 = m I 有向线段以速度ω按逆时针方向旋转 则:该旋转有向线段每一瞬时在纵轴上的投影即 表示相应时刻正弦量的瞬时值。 有向线段与横轴夹角 = 初相位  1 i 1 i ω t 0  x y O m I ψ i ω t O

称i=ILp 为正弦量) 对应的相量。 相量：表示正弦电量的幅值和初相角的复数。 设正弦量：u=Usin(ωt+w） 相量： U=Ue=ULv 相量的模=正弦量的有效值 (相量辐角=正弦量的初相角 09:41 25

09:41 25 相量: 相量的模=正弦量的有效值 相量辐角=正弦量的初相角   U Ue U j  设正弦量: u Um sin(ωt ) x y ω 1 i i0  A A’ O 相量:表示正弦电量的幅值和初相角的复数。 称   为正弦量 i(t)  I I 对应的相量