《电工技术》课程教学课件（课件讲稿）第4章 正弦交流电路

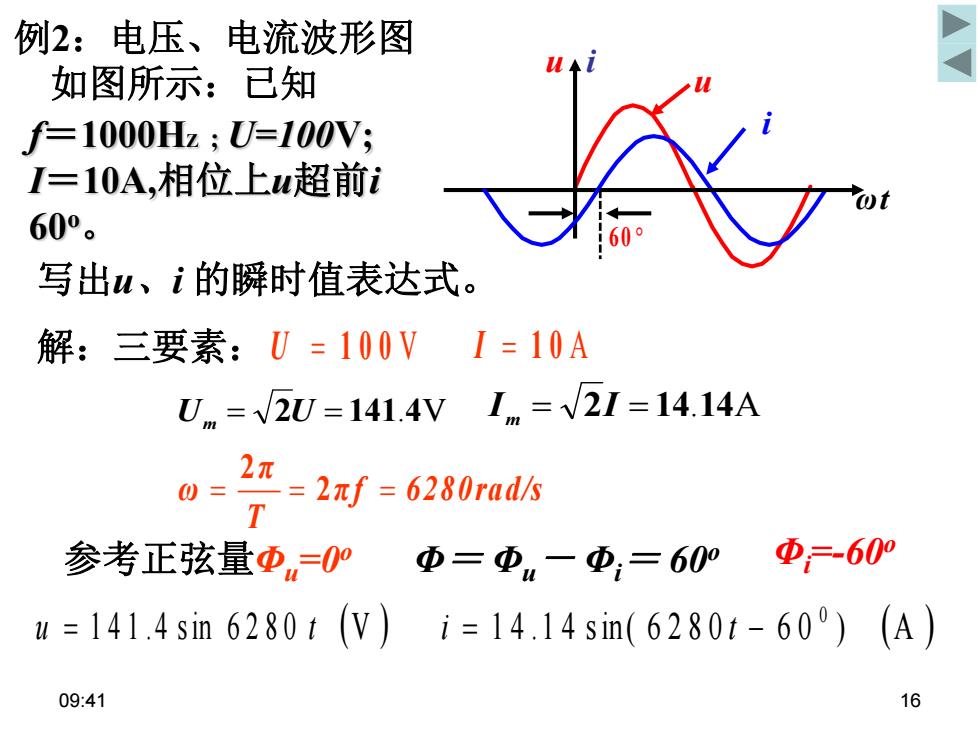
例2：电压、电流波形图 如图所示：已知 f=1000Hz;U=100V; 1I=10A,相位上u超前i 60°。 0 写出u、i的瞬时值表达式。 解：三要素：U=100VI=10A Um=V2U=141.4VIm=√2I=14.14A 2 0=27=2πf=6280rad5 T 参考正弦量Φ=0 Φ=Φ-Φ：=60° Φ=60 u=141.4sin6280t(Vi=14.14sin(6280t-600)(A) 09:41 16

09:41 16 i ωt u i 60  u 例2：电压、电流波形图 如图所示：已知 写出u、i 的瞬时值表达式。 f＝1000HZ ; U=100V; I＝10A,相位上u超前i 60o 。 Φi =-60o 参考正弦量Φu=0o U  100 V I  1 0 A 1 4 .1 4 s in ( 6 2 8 0 6 0 ) A  0 i  t - 解：三要素： u  141 .4 s in 6280 t V  U  2U  141.4V I m  2I  14.14A m π f 6280rad/s T π ω   2  2 Φ＝ Φu－ Φi ＝ 60o

可以证明同频率正弦波运算后，频率不变。 { w=100sin(wt+450) =60sin(wt-30) 儿=W1+W, =100sin(ot+45）+60sin(ot-30°） =129sin(ot+1821 幅值、相位变化 频率不变 结论： 因角频率（ω）不变，所以以下讨论同频率正弦波 时，ω可不考虑，主要研究幅值与初相位的变化。 09:41

09:41 17 可以证明同频率正弦波运算后，频率不变。 结论: 因角频率（）不变，所以以下讨论同频率正弦波 时， 可不考虑，主要研究幅值与初相位的变化。       ' sin sin sin 129 18 21 100 45 60 30 1 2         -   t t t u u u    幅值、相位变化 频率不变 如： ( ) ( ) 0 2 0 1 60 sin 30 100 sin 45 = - = + u t u t ω ω

4.2正弦量的相量表示法 4.2.1正弦量的表示方法 波形图 瞬时值表达式 必须 u(t)=U sin(ot+w） 小写 对正弦交流电路进行分析时，经常遇到正弦信号的 代数、微分和积分运算，用三角函数和波形图进行分 析运算繁杂不方便。 借用复数（矢量）表示正弦量（相量表示法）。 09:41 18

09:41 18 4.2 正弦量的相量表示法 瞬时值表达式 ut Um sin(t  ) 对正弦交流电路进行分析时,经常遇到正弦信号的 代数、微分和积分运算，用三角函数和波形图进行分 析运算繁杂不方便。 波形图 4.2.1 正弦量的表示方法 必须 小写 u O ωt 借用复数（矢量）表示正弦量（相量表示法）

复数可用有向线段表示 复数表示： +j 模 A=a+ib 代数式 =Al(cosw+jsin y叨 三角式 Al eiy . 指数式 +1 =A∠W 极坐标式 幅角 由欧拉公式， c0sw+jsin w=eΨ得出： 4=Va2+b2 复数在进行加减运算时应采用代数式， y=arctan b 实部与实部相加减，虚部与虚部相加减。 a=A cos v 复数在进行乘除运算时应采用指数式或 极坐标式，模与模相乘除，幅角与幅角 b=A sin w 相加减。 09:41 ▣出

09:41 19 复数可用有向线段表示 a A 0  b +1 +j |A| 模 幅角 a= |A| cos  b= |A| sin  |A| = a 2+b2  =arctan b a cos  +jsin  =ej 由欧拉公式， A=a+jb 代数式 三角式 指数式 极坐标式 复数表示： = |A|(cos  +jsin ) = |A| e j = |A|   复数在进行加减运算时应采用代数式， 实部与实部相加减，虚部与虚部相加减。 复数在进行乘除运算时应采用指数式或 极坐标式，模与模相乘除，幅角与幅角 相加减。 得出：

复数运算 A1=u1tb1=Al∠0 A2=2tjb2=A2l∠02 ·相等：a1=a2,b1=b2;A1=Al,01=82 A1=A2 加减：A1±A2=(a1士a2)+j(b1±b2) 相乘：A·=A∠0A2∠0=AA∠(0+O) +扩=0+jjA=1∠90·Al∠8=Al∠(0，+90) -j=0-i jA1=A1l∠(0-90) 相除：14=418=A∠(0-8) |A|∠82|AI 09:41 20

09:41 20 1 2 A A        A A A A ( ) 1 1 2 2 1 2 1 2     ( ) | | | | | | | | / 1 2 2 1 2 2 1 1 1 2       -    A A A A A A 相乘: 相除: • 加减：A1±A2= ( a1±a2 )+j (b1±b2 ) • 相等： a1 = a2 , b1 = b2；|A1 |= |A2 | ,  1 =  2 复数运算 •A1=a1+jb1= |A1 | 1 A2=a2+jb2 = |A2 |  2 +j=0+j j ·A1 =1∠90o · |A1 | 1 = |A1 | (1 + 90o ) -j=0-j -j ·A1= |A1 | (1 - 90o ) A1=A2