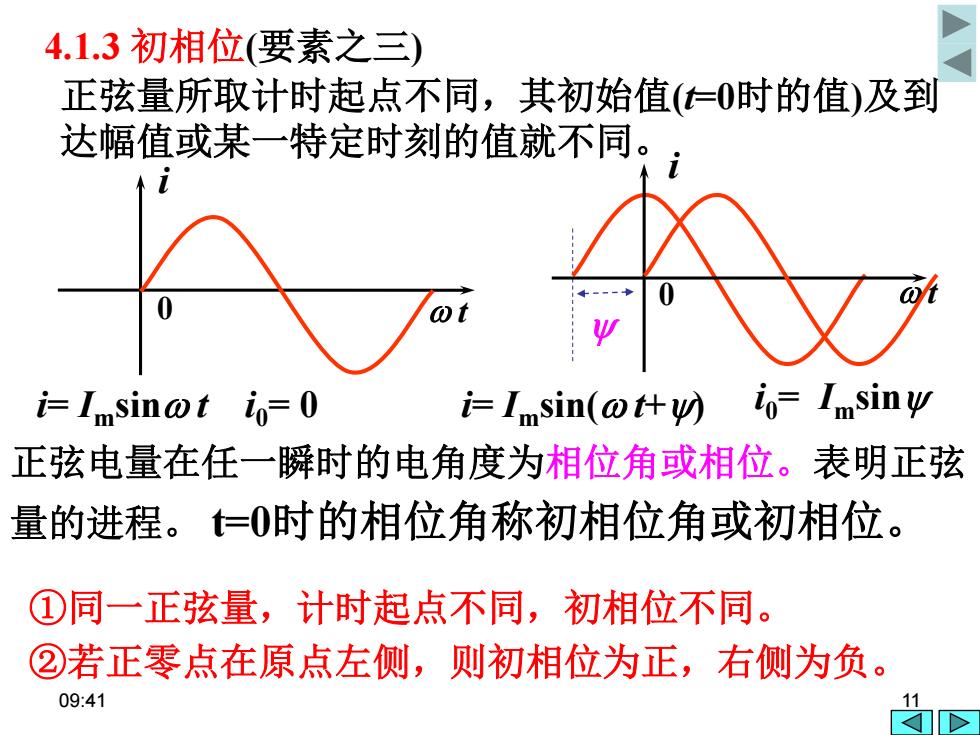
4.1.3初相位(要素之三) 正弦量所取计时起点不同,其初始值(仁0时的值)及到 达幅值或某一特定时刻的值就不同。 0 i=Imsinot i=0 i=Isin(ot什y吻io=Imsiny 正弦电量在任一瞬时的电角度为相位角或相位。表明正弦 量的进程。=0时的相位角称初相位角或初相位。 ①同一正弦量,计时起点不同,初相位不同。 ②若正零点在原点左侧,则初相位为正,右侧为负。 09:41 11
09:41 11 4.1.3 初相位(要素之三) ①同一正弦量,计时起点不同,初相位不同。 ②若正零点在原点左侧,则初相位为正,右侧为负。 i= Imsin t i= Imsin( t+) 正弦量所取计时起点不同,其初始值(t=0时的值)及到 达幅值或某一特定时刻的值就不同。 t i 0 i 0 t i0= 0 i0= Imsin 正弦电量在任一瞬时的电角度为相位角或相位。表明正弦 量的进程。 t=0时的相位角称初相位角或初相位
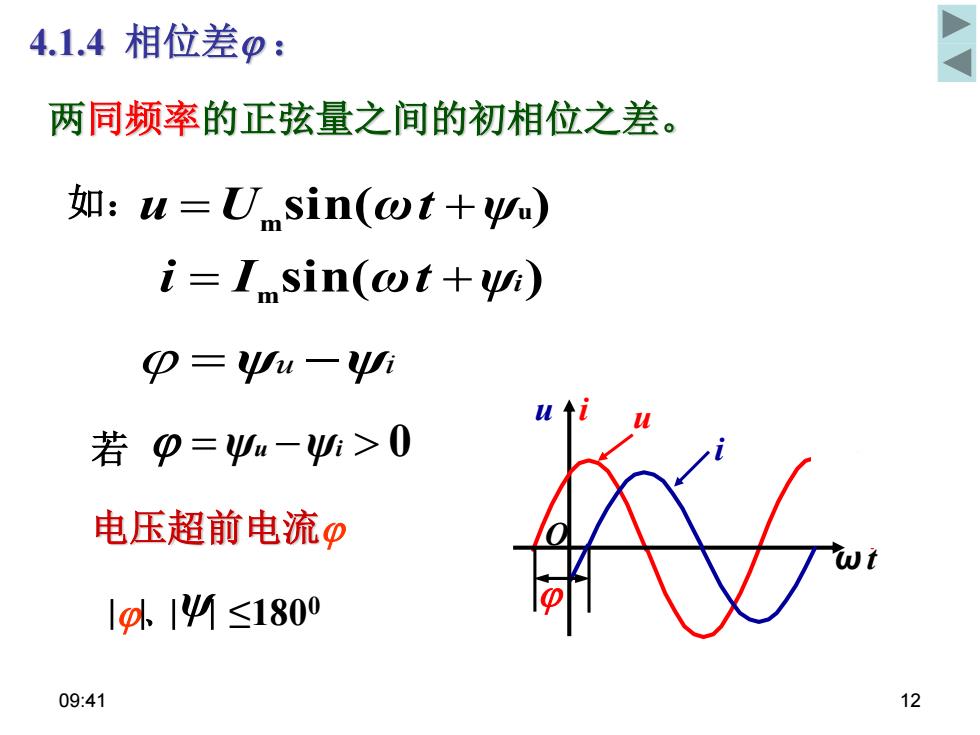
4.1.4相位差p: 两同频率的正弦量之间的初相位之差。 如:u=U sin(wt+u) i=I sin(ot+y) p=Ψu一Ψn 若p=必m-4>0 电压超前电流p lg4I4≤1800 09:41 12
09:41 12 sin( u) 如: u U m ωt ψ - ψu i ψ 若 ψu -ψi 0 电压超前电流 两同频率的正弦量之间的初相位之差。 4.1.4 相位差 : sin( ) m i I ωt ψi u i u i ω t O ﹑ ψ ≤1800

P=业a-<0 p=Ψm-=180° 电流超前电压p 电压与电流反相 p=Ψm-i=0 电压与电流同相 当两个同频率的正弦 量计时起点改变时, 它们的初相位角改变, 但初相角之差不变。 09:41 13
09:41 13 电压与电流同相 ψu -ψi 0 电流超前电压 ψu -ψi 0 u i ω t u i O ω t u i u i O u i ω t u i O 电压与电流反相 ψu -ψi 180 当两个同频率的正弦 量计时起点改变时, 它们的初相位角改变, 但初相角之差不变
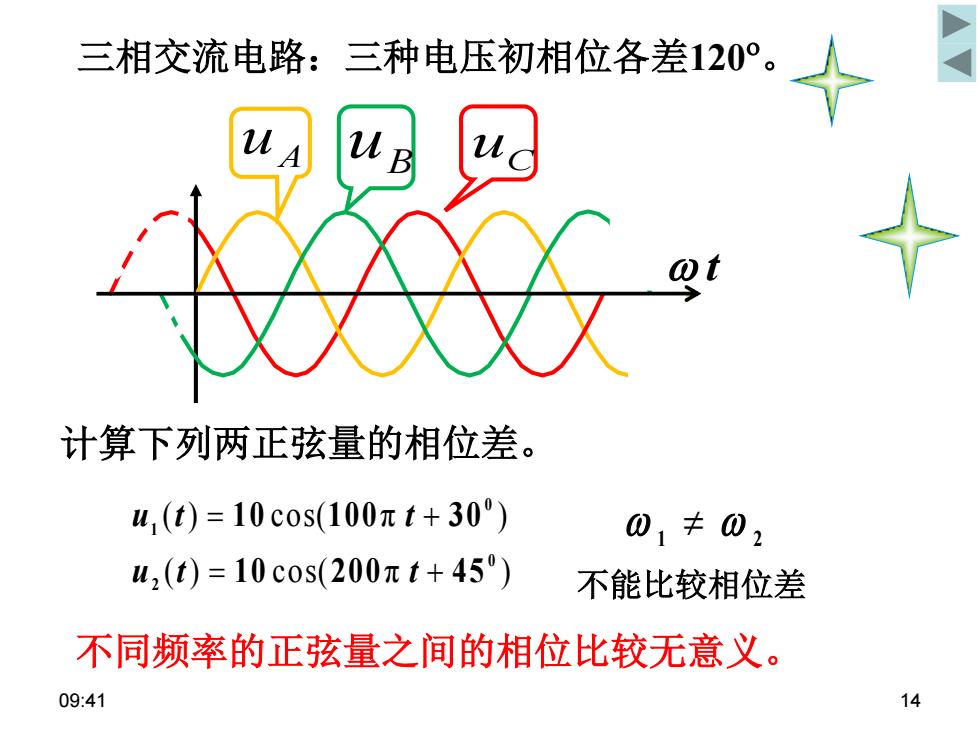
三相交流电路:三种电压初相位各差120°。 计算下列两正弦量的相位差。 u,(t)=10c0s(100πt+30) 01丰0, u,(t)=10c0s(200πt+45) 不能比较相位差 不同频率的正弦量之间的相位比较无意义。 09:41 14
09:41 14 不同频率的正弦量之间的相位比较无意义。 三相交流电路:三种电压初相位各差120 。 A uB uC u t ( ) cos( π ) ( ) cos( π ) 0 2 0 1 1 0 200 4 5 1 0 100 3 0 u t t u t t 不能比较相位差 1 2 计算下列两正弦量的相位差

例1:电压、电流波形图 如图所示: 已知 100V 0=6280rad/s 写出u、i的瞬时值表达式; W i 计算、之间的相位差。 解:三要素:Um=100VIm=10A 0=6280rad/s Φ=+60°Φ=一30 i=10sin(6280t+60)A u=100sin(6280t-30)V Φ=Φ4-Φ=一30一600=-900 即u落后i90 09:41 15
09:41 15 u i ω t u i 60 O o 30o 10A 100V Φi=+60o Φu =-30o U m 100 V I m 1 0 A s in ( ) A 0 i 1 0 6280 t 6 0 ω=6280 rad/s 写出u、i 的瞬时值表达式; 计算u、i之间的相位差。 解:三要素: 例1:电压、电流波形图 如图所示:已知 ω=6280 rad/s u s in ( ) V 0 1 0 0 6 2 8 0 t - 3 0 Φ= Φu- Φi = -30o -60o=-90o 即 u 落后 i 90o