
带限信道的信号设计 假设: ●带限信道具有理想频率响应特性。当fs时,C=1 ●脉冲x()具有谱特性X(f)=|G(f x(t)=x(N)emndr 由于: y=1+∑1nxn+y n=0 n≠K 无符号间干扰的条件是: 1 x(=KT)=x=0 k=0 k≠0 定理(奈奎斯特脉冲成形准则) 使0满足x()= n=0 0 n≠0 的充要条件是其傅里叶变换X(f)应满足: ∑X(f+m/T)=T 11
11 使 x(t)满足 ( ) 的充要条件是其傅里叶变换 X( f ) 应满足: 1 0 0 0 n x nT n = = 假设: ⚫带限信道具有理想频率响应特性。当 | f |w时,C(f)=1 ⚫脉冲x(t)具有谱特性 ( ) ( ) 2 X f = G f ( ) ( ) 2 w j ft w x t X f e df − = k n k n k n k k n y = I + I x + v − = 0 ( ) 1 0 0 0 k k x t kT x k = = = = 由于: 无符号间干扰的条件是: 定理(奈奎斯特脉冲成形准则) X ( f m T ) T m + = =− / 带限信道的信号设计

带限信道的信号设计 证明: x0)=°X(f2df 仁nT时刻: x(nT)=X(fy2rd所 积分区间分解成若干长度为1T的小区间: x0))=立x(2r 11 =2∫X(f+m/T)e2xrd =[三x+m)p df = B(f)emdf 式中:BU)=∑XU+m/T) 是周期为1T的周期函数 12
12 证明: t=nT 时刻: x(nT) X ( f )e df j2fnT − = ( ) ( ) 2 1) 2 (2 1) m T j fnT m T m x nT X f e df + − =− = ( ( ) ( ) =− = + m B f X f m /T 积分区间分解成若干长度为1/T的小区间: 式中: 是周期为1/T的周期函数 x(t) X ( f )e df j2ft − = 带限信道的信号设计 ( ) 1/ 2 2 1/ 2 / T j fnT T m X f m T e df − =− = + ( ) 1/ 2 2 1/ 2 / T j fnT T m X f m T e df − =− = + ( ) 1/ 2 2 1/ 2 T j fnT T B f e df − =
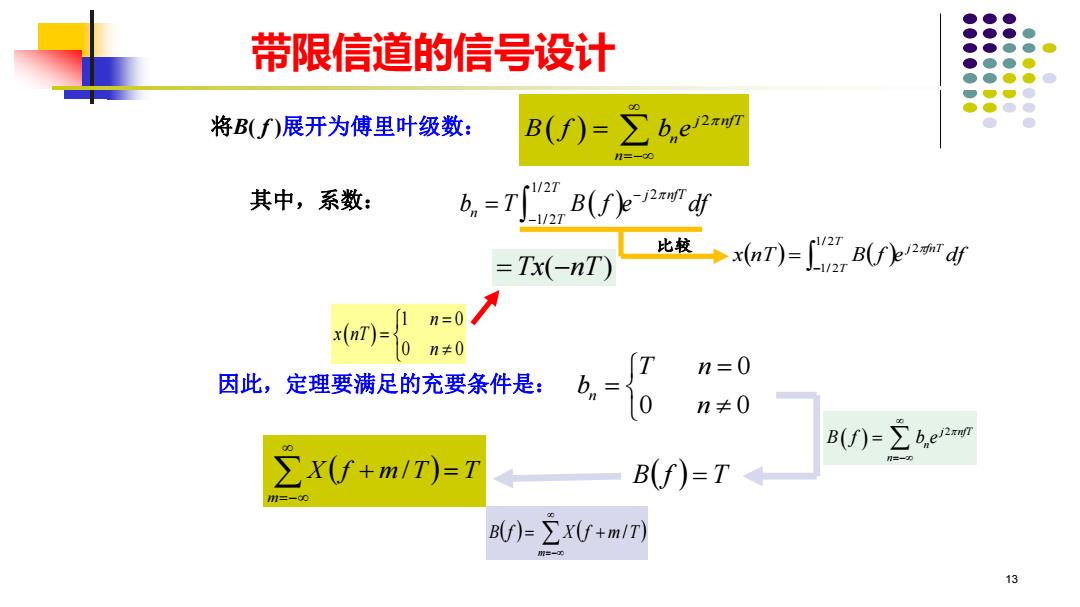
带限信道的信号设计 将B(f)展开为傅里叶级数: B(f)=∑b,e2mr 其中,系数: 6.-T B(fedf =Tx(-nT) 比较→xnT)=BU水2rd n=0 因此,定理要满足的充要条件是:么,=。 n=0 n≠0 B()=>b.el ∑X(U+m/T)=T B(f)=T BU)=∑xU+m/T) 13
13 将B( f )展开为傅里叶级数: ( ) j nfT 2 n n B f b e =− = ( ) 1/ 2 2 1/ 2 T j nfT n T b T B f e df − − = 其中,系数: ( ) ( ) 2 1/ 2 1/ 2 x nT B f e df j fnT T T − = = − Tx nT ( ) 0 0 0 n T n b n = = 因此,定理要满足的充要条件是: X ( f m T ) T B( f ) = T m + = =− / ( ) j nfT 2 n n B f b e =− = ( ) ( ) =− = + m B f X f m /T 带限信道的信号设计 ( ) 1 0 0 0 n x nT n = = 比较
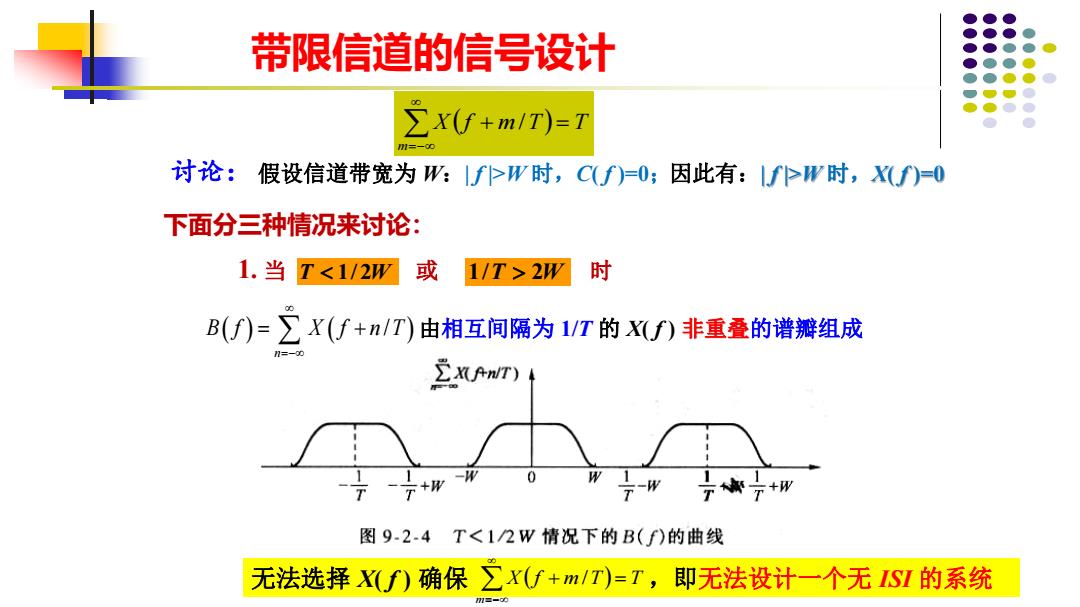
带限信道的信号设计 ∑X(f+m/T)=T 讨论: 假设信道带宽为W:If>W时,C(f)=O;因此有:fPW时,X(f)=0 下面分三种情况来讨论: 1.当T<1/2W 或 1/T>2W 时 B(f)=∑X(f+n/T)由相互间隔为1VT的f)非重叠的谱瓣组成 三AmT) + 图9-2.4T<1/2W情况下的B(f)的曲线 无法选择X(f)确保∑X(f+m/T)=T,即无法设计一个无IS的系统
14 1. 当 或 时 讨论: 假设信道带宽为 W:| f |>W 时,C( f )=0; T W 1/ 2 1/ 2 T W 由相互间隔为 1/T 的 X( f ) 非重叠的谱瓣组成 无法选择 X( f ) 确保 ,即无法设计一个无 ISI 的系统 下面分三种情况来讨论: 带限信道的信号设计 因此有:| f |>W 时,X( f )=0 X ( f m T ) T m + = =− / X ( f m T ) T m + = =− / ( ) ( / ) n B f X f n T =− = +