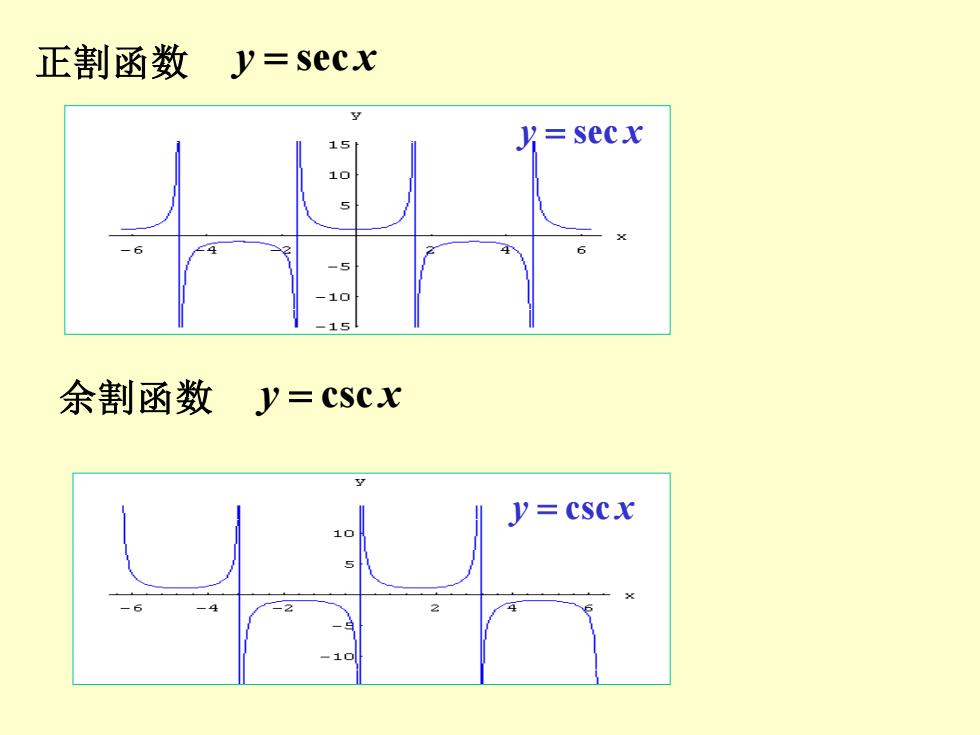
正割函数y=secx 15 y=secx 10 10 余割函数y=CsCx y=cscx 1口 10
正割函数 y = sec x y = sec x 余割函数 y = csc x y = csc x
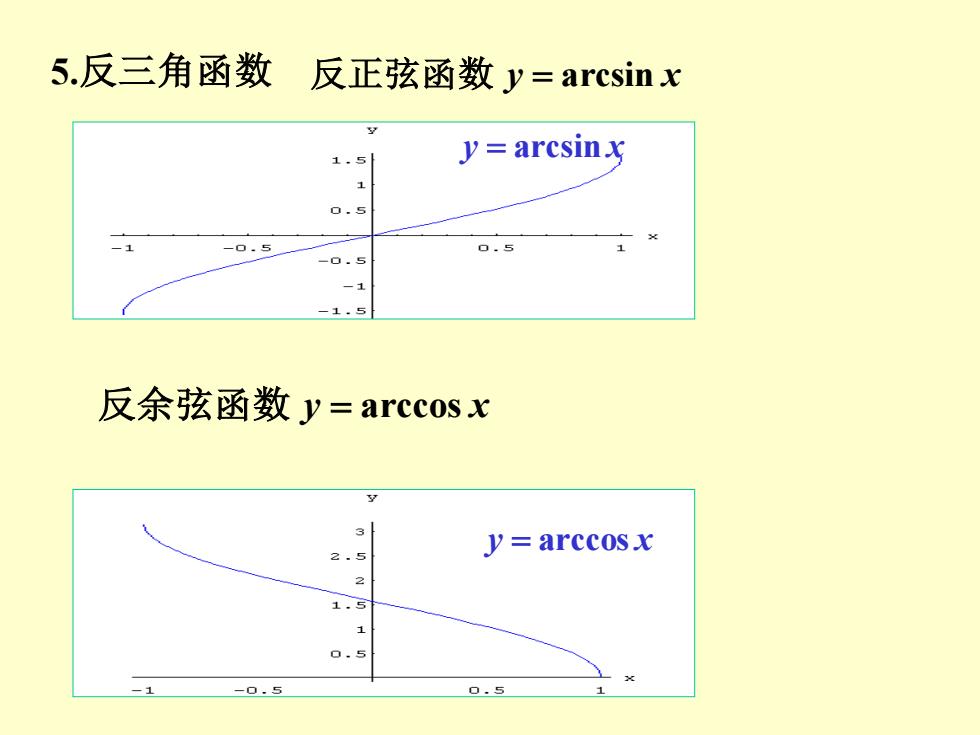
5.反三角函数 反正弦函数y=arcsinx 1.5 y=arcsinx 1 0.s -0.5 0.5 -0.5 -1 1.5 反余弦函数y=arccosx y=arccosx 2.5 2 1.5 1 0.5 一1 -0.5 0.5
5.反三角函数 反正弦函数 y = arcsin x y = arcsin x 反余弦函数 y = arccos x y = arccos x
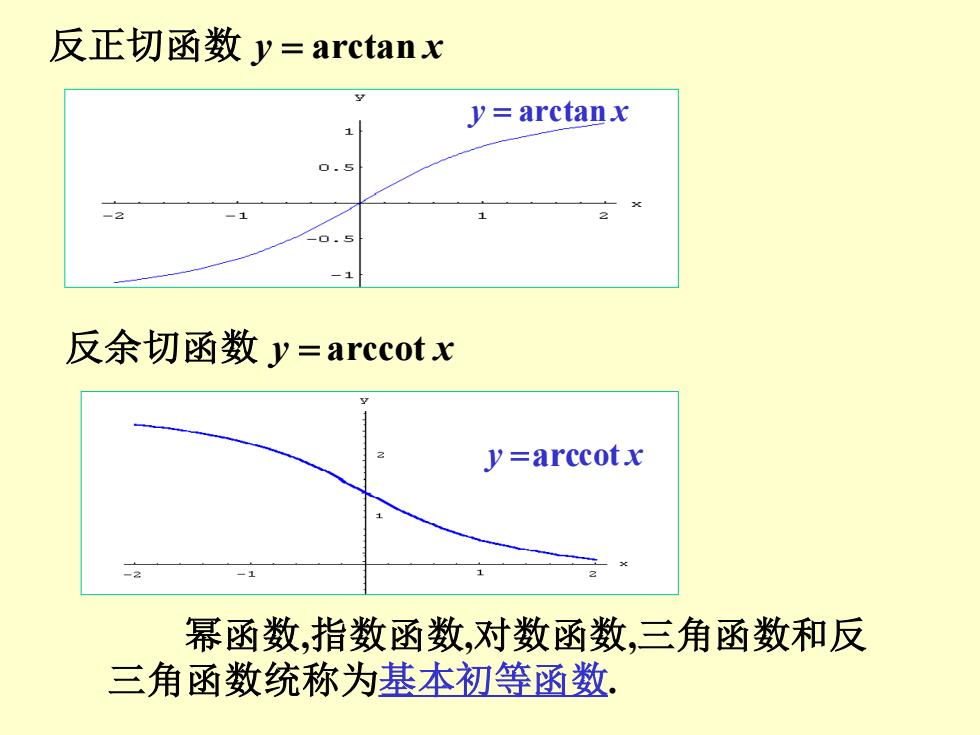
反正切函数y=arctanx y=arctanx 0.5 反余切函数y=arccotx y=arccotx 幂函数,指数函数,对数函数,三角函数和反 三角函数统称为基本初等函数
反正切函数 y = arctan x y = arctan x 反余切函数 y = arccot x y =arccot x 幂函数,指数函数,对数函数,三角函数和反 三角函数统称为基本初等函数

二、复合函数初等函数 1.复合函数 在实标问题中,有很多比较复杂的函数是由几个 比较简单的函数“叠置”而成的,如在简谐振动中 位移y与时间t的函数关系 y sin(at+p) 就是由三角函数y=sinw和线性函数u=ot+p “叠置”而成的, 设y=u,h=1-x2,→y=√1-x2
二、复合函数 初等函数 1.复合函数 在实际问题中,有很多比较复杂的函数是由几个 比较 简单的函数“叠置”而成的,如在简谐振动中 位移y与时间 t 的函数关系 y = sin(t +) 就是由三角函数 y = sin u 和线性函数 u = t + “叠置”而成的, 设 y = u, 1 , 2 u = − x 2 y = 1 − x