第二章导数与微分 2.1导数的概念 2.1.1两个实例 1、变速直线运动 我们如道,求物体作匀直线运动的速度有公式;(其中5表示路程。t表示 时间).但如果是求变速直线运动的解时速度就无法用这个公式,此时我们可以先考虑时间 区间,+△内的平均速度了=飞+-,显然当-0时,T(如果存在) 4 即是物体在时刻,时的瞬时速度。=mF=网化+A-。 △M 2、曲线切线的斜率 如图2.1.1,曲线在点x处的切线M,T为当割线MM绕着切点M。旋转至切线位置 MT时的直线, l/ 人1 x0+△rx 图2.1.1 则车=ma一回是一儿伍+型(哭极斑在的话. 2.1.2导数的概念 以上两例是变速直线运动的瞬时速度和曲线切线的斜率的具体问题,由此可抽象出导数 的概念。 △y 定义1:设函数f)在点。及其近旁有定义,若极限巴存在,则此极限称为函数 20
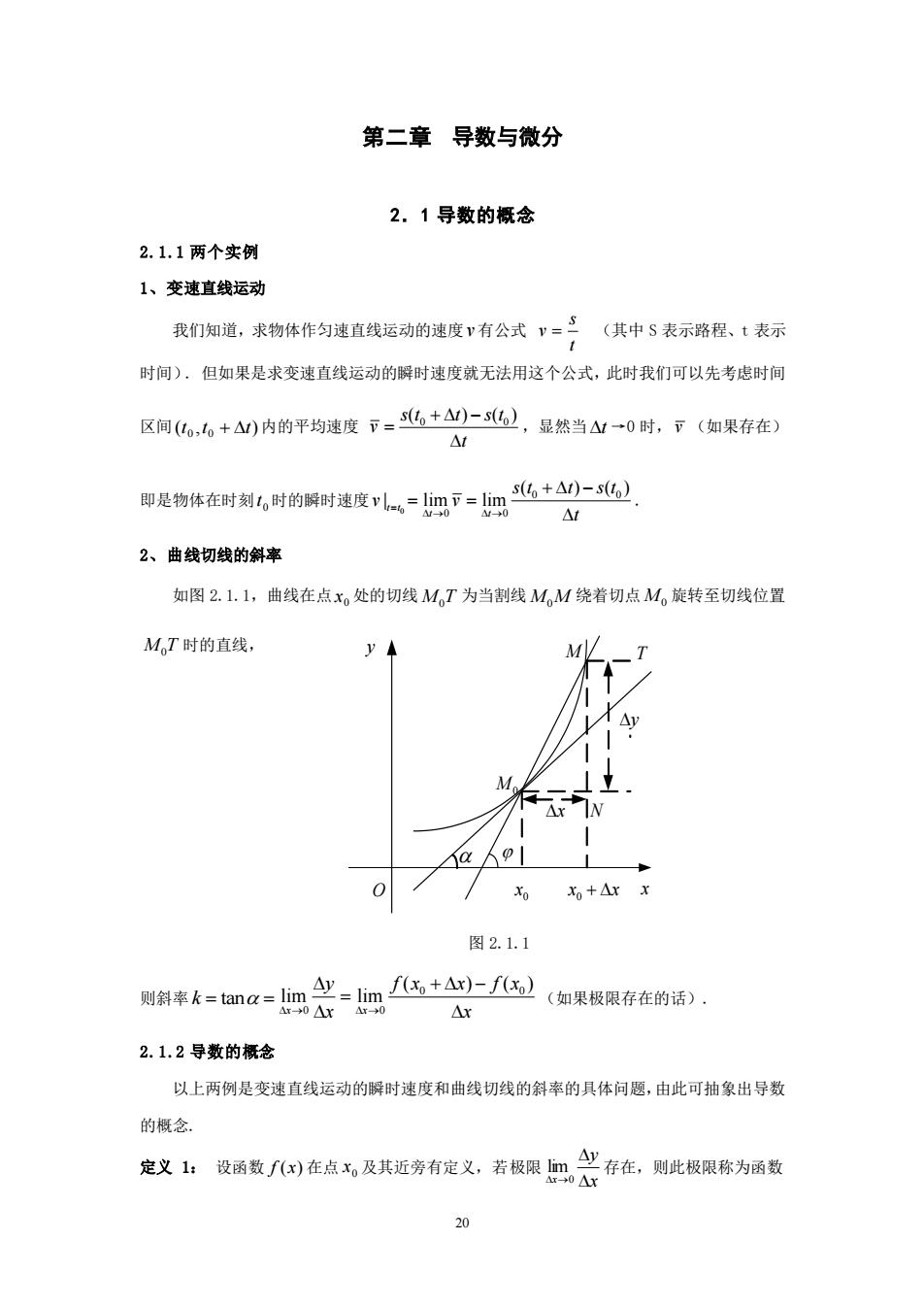
20 第二章 导数与微分 2.1 导数的概念 2.1.1 两个实例 1、变速直线运动 我们知道,求物体作匀速直线运动的速度 v 有公式 t s v = (其中 S 表示路程、t 表示 时间). 但如果是求变速直线运动的瞬时速度就无法用这个公式,此时我们可以先考虑时间 区间 ( , ) 0 0 t t + t 内的平均速度 0 0 s t t s t ( ) ( ) v t + − = ,显然当 t →0 时, v (如果存在) 即是物体在时刻 0 t 时的瞬时速度 0 0 0 0 0 ( ) ( ) | lim lim t t t t s t t s t v v t = → → + − = = . 2、曲线切线的斜率 如图 2.1.1,曲线在点 0 x 处的切线 M T0 为当割线 M M0 绕着切点 M0 旋转至切线位置 M T0 时的直线, 图 2.1.1 则斜率 k = = tan 0 0 0 0 ( ) ( ) lim lim x x y f x x f x → → x x + − = (如果极限存在的话). 2.1.2 导数的概念 以上两例是变速直线运动的瞬时速度和曲线切线的斜率的具体问题,由此可抽象出导数 的概念. 定义 1: 设函数 f (x) 在点 0 x 及其近旁有定义,若极限 x y x →0 lim 存在,则此极限称为函数 x O x + x 0 0 x M0 M T N y x y

f(x)在点x。处的导数(或称f(x)在点x。处可导,否则称f(x)在点x。处不可导).记作 1·密政l dx -是=+-四 x-x。 定义2:若函数f(x)在区间(a,b)内点点可导,则称函数f(x)在(a,b)内可导:又若f(a) 和f(b)存在,则称函数f(x)在闭区间[a,b1上可导. 其种)典二.f)=分别为商数阳 x-xo x-xo 在点x。处的左、右导数 若函数f(x)在区间(a,b)内点点可导,这时,对于(a,b)内的每一点x,必存在一个导 数与之对应,这样就确定了一个新的函数,称为函数∫(x)的导函数,简称为导数。记作 f,y,田 dx 导数的几何意义:f"(x)的几何意义是曲线y=f(x)在点(xo,f(x》处的切线的斜 率,即 k=tana=f'(xo)】 因此,曲线y=f(x)在点(xo,f(x》处的切线方程为 y-f(xo)=f'(xoXx-xo). 法线方程为 -=7-)*0, 例1求y=x2在x=1点处的导数. 0=色是-血+-四 △r
21 f (x) 在点 0 x 处的导数(或称 f (x) 在点 0 x 处可导,否则称 f (x) 在点 0 x 处不可导). 记作 ( ) 0 f x , 0 x x y = , 0 x x dx dy = 或 0 ( ) x x dx df x = . 即 ( ) 0 f x x y x = →0 lim x f x x f x x + − = → ( ) ( ) lim 0 0 0 0 0 ( ) ( ) lim 0 x x f x f x x x − − = → . 定义 2:若函数 f (x) 在区间 (a,b) 内点点可导,则称函数 f (x) 在 (a,b) 内可导;又若 f (a) + 和 f (b) − 存在,则称函数 f (x) 在闭区间 [a,b] 上可导. 其中 ( ) 0 f x − 0 0 ( ) ( ) lim 0 x x f x f x x x − − = → − , ( ) 0 f x + 0 0 ( ) ( ) lim 0 x x f x f x x x − − = → + 分别称为函数 f (x) 在点 0 x 处的左、右导数. 若函数 f (x) 在区间 (a,b) 内点点可导,这时,对于 (a,b) 内的每一点 x ,必存在一个导 数与之对应,这样就确定了一个新的函数,称为函数 f (x) 的导函数,简称为导数. 记作 f (x) , y , dx dy 或 dx df (x) . 导数的几何意义: ( ) 0 f x 的几何意义是曲线 y = f (x) 在点 ( , ( )) 0 0 x f x 处的切线的斜 率,即 tan ( ) 0 k = = f x . 因此,曲线 y = f (x) 在点 ( , ( )) 0 0 x f x 处的切线方程为 ( ) ( )( ) 0 0 0 y − f x = f x x − x . 法线方程为 ( ) ( ) 1 ( ) 0 0 0 x x f x y f x − − − = ( f (x0 ) 0 ). 例 1 求 2 y x = 在 x = 1 点处的导数. 解 f (1) = x y x →0 lim x f x f x + − = → (1 ) (1) lim 0

-+-12t-2 △r 例2试判定函数=中x之0在点x=0处是香可导, xx<0 幕0=10=0-pw f0=®f0=p1 X y化收8ee9 2.1.3导数与连续的关系 定义一极限一连续一导数,这是函数f(x)在点x。处四个概念之间的关系,但反 之却不然.即在点x。处可导必连续,连续不一定可导:不连续必不可导. 例3证明函数y=x在点x=0处连续但不可导. 证明 lim f(x)=lim=0=f(0). 所以,函数y=冈在点x=0处连续。 0=g:/0-=1. E0=:/0=m子=1 X 所以,函数y=冈在点x=0处不可导。 练习题2.1 1.求下列曲线在指定点处的切线方程和法线方程. (1)y=lnx在点(e,1)处: @e匠当是 2.物体作直线运动,运动方程为s=32-51,求: (1)物体在1秒到1+△秒的平均速度: (2)物体在1。到1+1。秒的平均速度:
22 2 0 (1 ) 1 lim x x → x + − = 2 0 2 lim x x x → x + = = 2 . 例 2 试判定函数 1 0 0 x x y x x + = 在点 x = 0 处是否可导. 解 f (0) 1 = , − (0) = ' f x f x f x ( ) (0) lim 0 − → − 0 1 lim x x x → − − = = + , + (0) = ' f x f x f x ( ) (0) lim 0 − → + 0 1 1 lim 1 x x x → + + − = = . 所以,函数 1 0 0 x x y x x + = 在点 x = 0 处不可导. 2.1.3 导数与连续的关系 定义 极限 ←连续 ←导数. 这是函数 f (x) 在点 0 x 处四个概念之间的关系,但反 之却不然. 即在点 0 x 处可导必连续,连续不一定可导;不连续必不可导. 例 3 证明函数 y = x 在点 x = 0 处连续但不可导. 证明 lim ( ) lim 0 (0) 0 0 f x x f x x = = = → → , 所以,函数 y = x 在点 x = 0 处连续. 但 + (0) = ' f x f x f x ( ) (0) lim 0 − → + lim 1 0 = = → + x x x , − (0) = ' f x f x f x ( ) (0) lim 0 − → − lim 1 0 = − − = → − x x x . 所以,函数 y = x 在点 x = 0 处不可导. 练习题 2.1 1.求下列曲线在指定点处的切线方程和法线方程. (1) y x = ln 在点(e,1)处; (2) y x = cos 在点 2 ( , ) 4 2 处. 2.物体作直线运动,运动方程为 2 s t t = − 3 5 ,求: (1)物体在 1 秒到 1+t 秒的平均速度; (2)物体在 0 t 到 0 t t + 秒的平均速度;

(3)物体在1。秒的速度. 3.讨论函数=十不>0在点x=0处的连续性和可导性 1-x,x≤0 2.2直接求导法 利用导数的定义(求增量、算比值、取极限),可以求得∫(x)在点x的导数。 例1求函数y=log。x的导数. 解(D求增量:4y=f八+A-f)=ogx+Ar)-bg。x=bg.1+A): ②第盒:g.e,0+ -g.0+4 (取概限y只-g0+当在-g,ea (log.)=xina' 转地,当a=时,有仙小- 例2求函数y=sinx的导数. 解(1)求增量:△y=fx+△x)-fx)=sn(+△x)-sinx -2o+An+5=2m+7m ②)算比值:g.20or+空m" 2 △x 2=c0r+4m 2△r 强r老+当芝 2r 2 2=cosx 2 即
23 (3)物体在 0 t 秒的速度. 3.讨论函数 − + = , , x x f x 1 1 ( ) 0 0 x x 在点 x = 0 处的连续性和可导性. 2.2 直接求导法 利用导数的定义(求增量、算比值、取极限),可以求得 f (x) 在点 x 的导数. 例 1 求函数 loga y x = 的导数. 解 (1)求增量: y = f (x + x)− f (x) (x x) x a a = log + −log log (1 ) x x a = + ; (2)算比值: x x x x y a + = log (1 ) x x a x x x = log (1+ ) 1 ; (3)取极限: 0 0 lim lim → → = = x x x y y x x a x x x log (1+ ) 1 1 1 log ln a e x x a = = , 即 1 (log ) ln a x x a = . 特别地,当 a e = 时,有 ( ) 1 ln ' x x = . 例 2 求函数 y = sin x 的导数. 解 (1)求增量: y = f (x + x)− f (x) = sin(x +x)−sin x ( ) ( ) 2 sin 2 2cos x + x + x x + x − x = 2 )sin 2 2cos( x x x = + ; (2)算比值: x x x x x y + = 2 )sin 2 2cos( 2 2 sin ) 2 cos( x x x x = + ; (3)取极限: x y y x = →0 lim 2 2 sin ) 2 lim cos( 0 x x x x x = + → x x x x x x x cos 2 2 sin ) lim 2 lim cos( 0 0 = = + → → , 即

(sinx)'=cosx. 同理可得 (cosx)'=-sinx 类似地,我们可以得到一些常用的求导基本公式: (1)C=0(c为常数): (2)(xy=ax-: (3)(a')=a'na, (4)(ey=e: (5)(log.)-xind 1 6)a-: (7)(sinx)'=cosx: (8)(cosx)'=-sinx: (9)(tanx)'=sec2x: (10)(cotx)'=-csc2x: (11)(secx)'=secxtanx (12)(cscx)=-cscxcotx: 1 1 (13)(arcsinx)'= VI-x (14)(arccosx)'=- V-x (15)(arctanx)= 1 (16)(arccotx)=- 导数的基本公式是由常数和基本初等函数的导数构成:六个三角函数相互搭档且正负相 间:四个反三角函数两两结论相同而符号相反, 导数的四则运算法则:设函数=u(x),v=v(x)在点x处都是可导的,则有 (1)(u±)=±v': (2)(6m)=r+m'; (3)(cw)=cW(c为常数): w月=-w*0 利用求导基本公式和四则运算法则,求得导数的方法叫作直接求导法。 例3求爵数y=号-+石的导数 房:米福y的9版
24 (sin ) cos x x = . 同理可得 (cos ) sin x x = − . 类似地,我们可以得到一些常用的求导基本公式: (1) c = 0 ( c 为常数); (2) 1 ( ) x x − = ; (3) (a ) a a x x = ln , (4) ( )x x e e = ; (5) 1 (log ) ln a x x a = , (6) ( ) 1 ln x x = ; (7) (sin ) cos x x = ; (8) (cos ) sin x x = − ; (9) x x 2 (tan ) = sec ; (10) ( ) 2 cot csc x x = − ; (11) (sec sec tan x x x ) = ; (12) (csc csc cot x x x ) = − ; (13) 2 1 (arcsin ) 1 x x = − ; (14) 2 1 (arccos ) 1 x x = − − ; (15) 2 1 (arctan ) 1 x x = + ; (16) 2 1 ( cot ) 1 arc x x = − + . 导数的基本公式是由常数和基本初等函数的导数构成;六个三角函数相互搭档且正负相 间;四个反三角函数两两结论相同而符号相反. 导数的四则运算法则:设函数 u u x = ( ) , v v x = ( ) 在点 x 处都是可导的,则有 (1) (u v) = u v ; (2) (uv) = u v + uv ; (3) (cu) = cu ( c 为常数); (4) 2 v u v uv v u − = ( v 0 ). 利用求导基本公式和四则运算法则,求得导数的方法叫作直接求导法. 例 3 求函数 3 2 3 x y x x x = − + 的导数. 解 3 3 4 2 3 x y x x = − + , 1 2 4 2 2 3 4 y x x x − = + + . 例 4 求函数 2 1 3 1 x y x + = + 的导数