《高等数学》课程教学资源（PPT课件）第十一章 曲线积分与曲面积分_第六节 对坐标的曲面积分_对坐标的曲面积分

>流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为立 单位时间内流向区域指定侧的流量Φ=A位， >有向曲面在坐标面上的投影 上述问题中，设=P+O+RX n=cosai+cosβj+cosyk Φ=AD·n=PAcosa+2 Acos B+RAcosy |Ac0sy|一A在xOy面上的投影区域的面积 Acosy一A在xOy面上的投影区域的面积的代数值 称Ac0Sy为A在xoy面上的投影. 分别称Acosa Ac0SB为4在voz面和z0x面上的投影

➢流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为v 单位时间内流向区域指定侧的流量  =  Av n ➢有向曲面在坐标面上的投影 v Pi Qj Rk = + + n i j k = + + cos cos cos     =  Av n= + + PA QA RA cos cos cos    | cos | A  A在xoy面上的投影区域的面积 Acos A在xoy面上的投影区域的面积的代数值 称 Acos 为A在xoy面上的投影. 分别称 Acos Acos  为A在yoz面和zox面上的投影. o x y z 上述问题中, 设 A n 

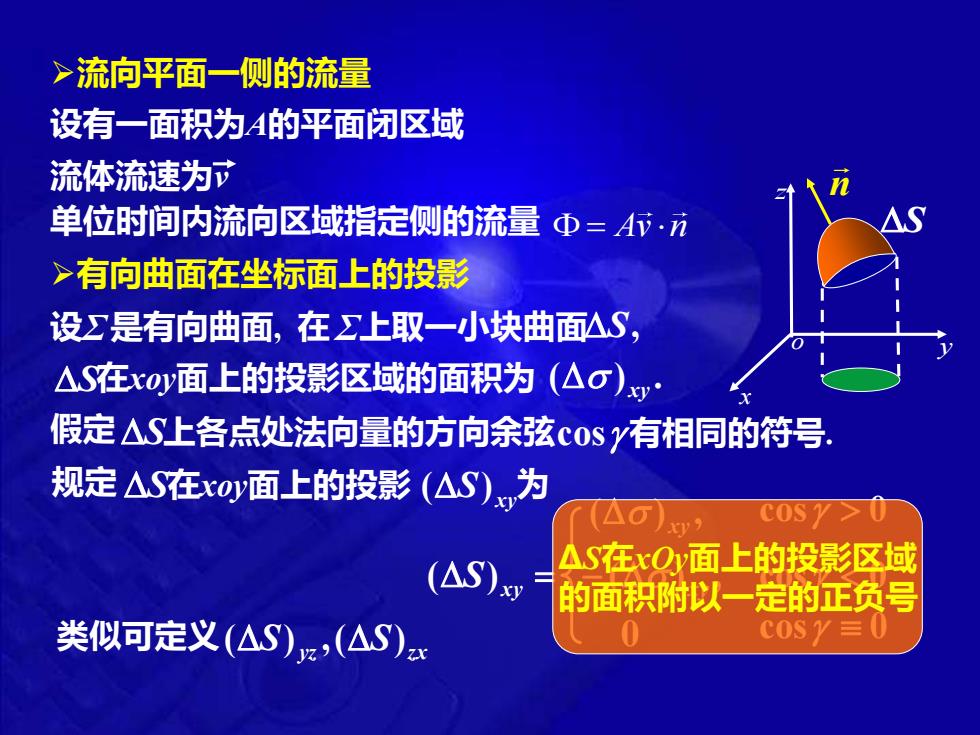
>流向平面一侧的流量 设有一面积为4的平面闭区域 流体流速为市 单位时间内流向区域指定侧的流量Φ=4行·方 >有向曲面在坐标面上的投影 设∑是有向曲面，在上取一小块曲面△S, △S在xOy面上的投影区域的面积为（△o)y· 假定△S上各点处法向量的方向余弦c0Sy有相同的符号. 规定△S在xoy面上的投影（△S)为 (△S)x AS在xOy面上的投影区域 的面积附以一定的正负号 类似可定义（△S),(△S): C0Sy≡U

➢流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为v 单位时间内流向区域指定侧的流量  =  Av n ➢有向曲面在坐标面上的投影 o x y z n  设 Σ 是有向曲面, 在 Σ 上取一小块曲面 S, S 在xoy面上的投影区域的面积为 ( ) .  xy 规定 S 在xoy面上的投影 S xy ( ) 为 (S) xy = ( ) ,  xy 假定 S 上各点处法向量的方向余弦 cos 有相同的符号. cos  0 ( ) , −  xy cos  0 0 cos  0 ΔS在xOy面上的投影区域 的面积附以一定的正负号 类似可定义 S yz S zx ( ) ,( ) S