
>曲面的侧 通过曲面上任一点处法向量的指向来指定 例:Σ:z=(x,y) n=-3,0cos7>0上侧 (3x,z,-1)c0sy<0下侧 ∑:x=x(y,z) -副 Σ:Jy=Jy(x,z i=-y1,-)cosB>0右侧 (y,-1,y)cosB<0左侧 有向曲面规定了侧的曲面
➢曲面的侧 通过曲面上任一点处法向量的指向来指定 例: = : ( , ) z z x y n = ( , ,1) x y − − z z cos 0 上侧 ( , , 1) x y z z − cos 0 下侧 = : ( , ) x x y z n = (1, , ) y z − − x x cos 0 前侧 ( 1, , ) y z − x x cos 0 后侧 = : ( , ) y y x z n = ( ,1, ) x z − − y y cos 0 右侧 ( , 1, ) x z y y − cos 0 左侧 o x y z o x y z o x y z ➢有向曲面 规定了侧的曲面

>流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为旷 单位时间内流向区域指定侧的流量Φ=? (位,)<
➢流向平面一侧的流量 设有一面积为A的平面闭区域 单位时间内流向区域指定侧的流量 = ? ( , ) 2 v n 流体流速为v

>流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为时 单位时间内流向区域指定侧的流量Φ=A位,方 心,m<2 V=A cos(,)=Ai
➢流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为v 单位时间内流向区域指定侧的流量 = Av n ( , ) 2 v n V A v v n Av n = = | | cos( , ) v n

>流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为下 单位时间内流向区域指定侧的流量Φ=A位, 低用=子V=0=4pjo反万
➢流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为v 单位时间内流向区域指定侧的流量 = Av n ( , ) 2 v n = V A v v n Av n = = = 0 | | cos( , ) v n
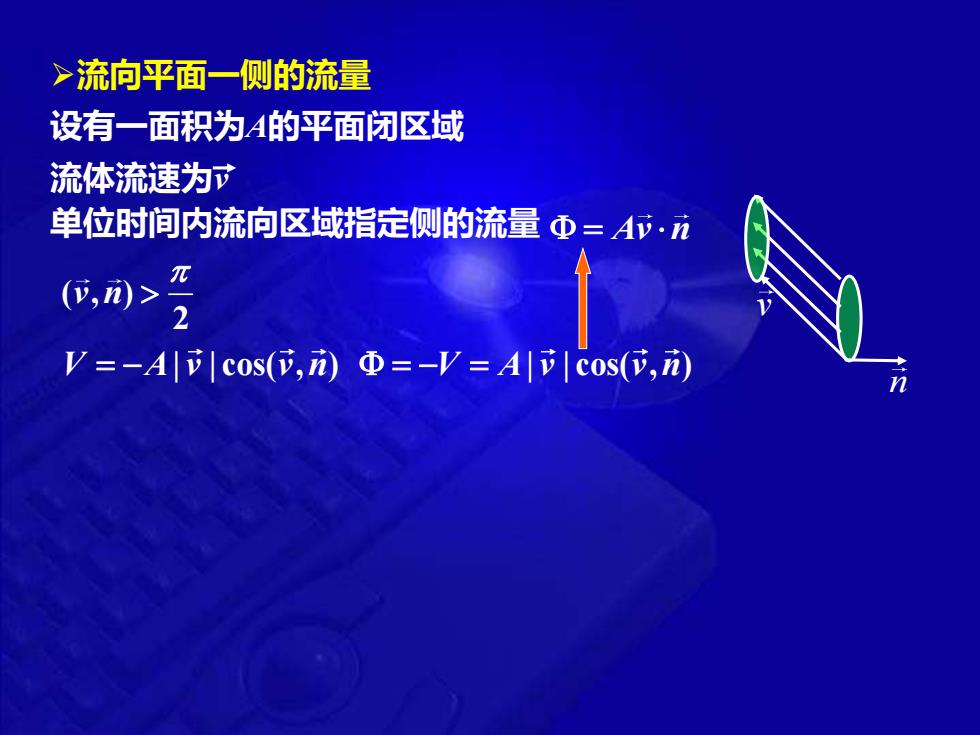
>流向平面一侧的流量 设有一面积为4的平面闭区域 流体流速为 单位时间内流向区域指定侧的流量Φ=A)· (,m>2 V=-A||c0s(位,)Φ=-V=A|币|c0s(正,)
➢流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为v 单位时间内流向区域指定侧的流量 = Av n ( , ) 2 v n V A v v n = − | | cos( , ) v n = − = V A v v n | | cos( , )