河套学院（河套大学）：《线性代数》课程教学资源（PPT课件讲稿）第二章 矩阵 2.5 初等变换与初等矩阵

人人 2.5.2 阶梯形矩阵 （续2) 尚本 阶梯形矩阵的特点是：可画出一条阶梯线， 线的下方全是零元素；每个台阶只有一行，台阶 数就是非零行的行数，每段台阶线上面的第一个 元素为非零元，也就是非零行的第一个非零元素， 3 如 三 河套大学《线性代数》课件 第二章矩阵 快东骨司

快乐学习 以人 2.5.2 阶梯形矩阵（续2） 为本 河套大学《线性代数》课件 第二章 矩阵 阶梯形矩阵的特点是：可画出一条阶梯线， 线的下方全是零元素；每个台阶只有一行，台阶 数就是非零行的行数，每段台阶线上面的第一个 元素为非零元，也就是非零行的第一个非零元素. 如 .               − − = 0 0 0 0 0 0 0 0 0 3 0 2 6 5 1 1 3 4 0 1 A

水人 2.5.3 最简形矩阵 尚本 定义2.5.3 满足下列两个条件的阶梯形矩阵 称为最简形矩阵： (1)矩阵的各首非零元素全为1， (2)矩阵的各首非零元素1所在列的上方元素 也全为零， 最简形矩阵的特点是：非零行的第一个非零元 素为1，且这些非零元素所在列的其他元素都是0. 河套大学《线性代数》课件 第二章矩阵 快乐骨司

快乐学习 以人 2.5.3 最简形矩阵 为本 河套大学《线性代数》课件 第二章 矩阵 定义2.5.3 满足下列两个条件的阶梯形矩阵 称为最简形矩阵 ： （1）矩阵的各首非零元素全为1； （2）矩阵的各首非零元素1所在列的上方元素 也全为零； 最简形矩阵的特点是：非零行的第一个非零元 素为1，且这些非零元素所在列的其他元素都是0

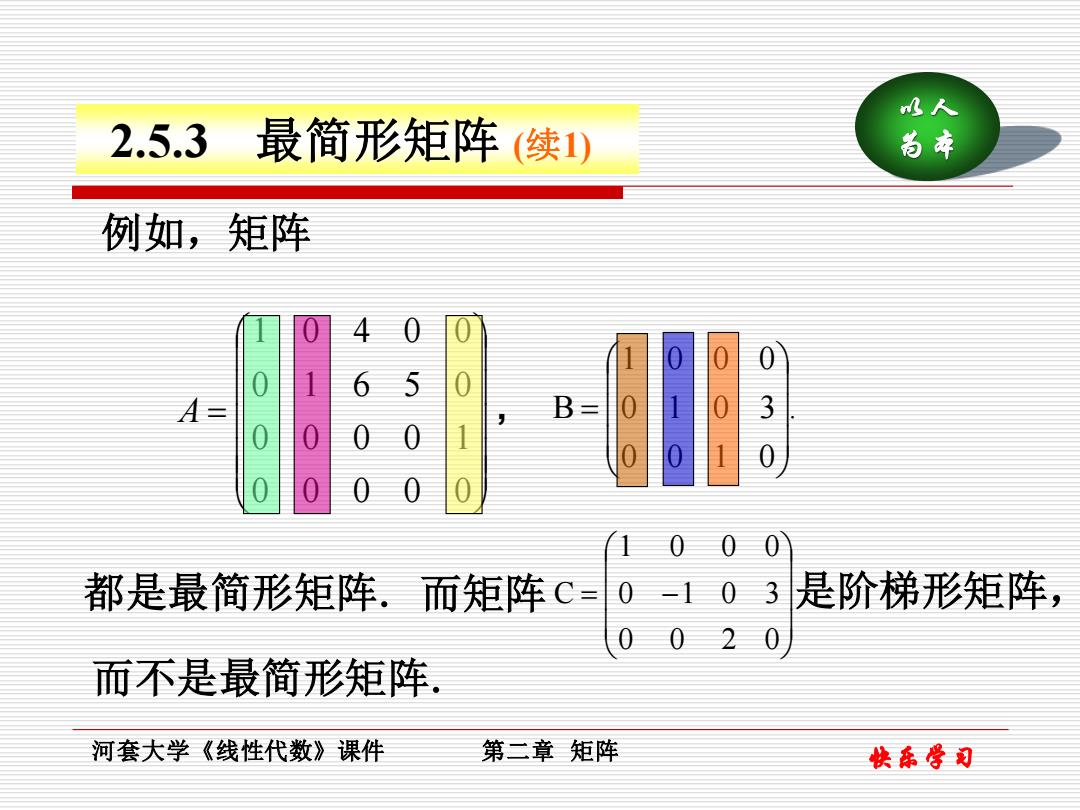
水人 2.5.3 最简形矩阵（续1） 尚本 例如，矩阵 4 0 A三 B 000 都是最简形矩阵.而矩阵C= 0-103 是阶梯形矩阵， 而不是最简形矩阵 河套大学《线性代数》课件 第二章矩阵 快东骨司

快乐学习 以人 为本 河套大学《线性代数》课件 第二章 矩阵 2.5.3 最简形矩阵 (续1) 例如，矩阵               = 0 0 0 0 0 0 0 0 0 1 0 1 6 5 0 1 0 4 0 0 A , . 0 0 1 0 0 1 0 3 1 0 0 0 B           = 都是最简形矩阵.           = − 0 0 2 0 0 1 0 3 1 0 0 0 而矩阵 C 而不是最简形矩阵. 是阶梯形矩阵

水人 2.5.4 初等矩阵 尚本 矩阵的初等变换是矩阵的一种最基本的运算， 它有着广泛的应用. 定义2.5.4对单位阵E进行一次初等变换所得 到的矩阵称为初等矩阵 对应于三类初等变换有三种类型的初等矩阵 (1)对调单位矩阵两行或两列 把单位矩阵E中第、两行对调（→）得初等 矩阵 河套大学《线性代数》课件 第二章矩阵 快乐骨司

快乐学习 以人 为本 河套大学《线性代数》课件 第二章 矩阵 2.5.4 初等矩阵 矩阵的初等变换是矩阵的一种最基本的运算 ， 它有着广泛的应用. 定义2.5.4 对单位阵 E 进行一次初等变换所得 到的矩阵称为初等矩阵. 对应于三类初等变换有三种类型的初等矩阵. （1）对调单位矩阵两行或两列 E i、j ( ) i j 把单位矩阵 中第 两行对调 r  r 得初等 矩阵

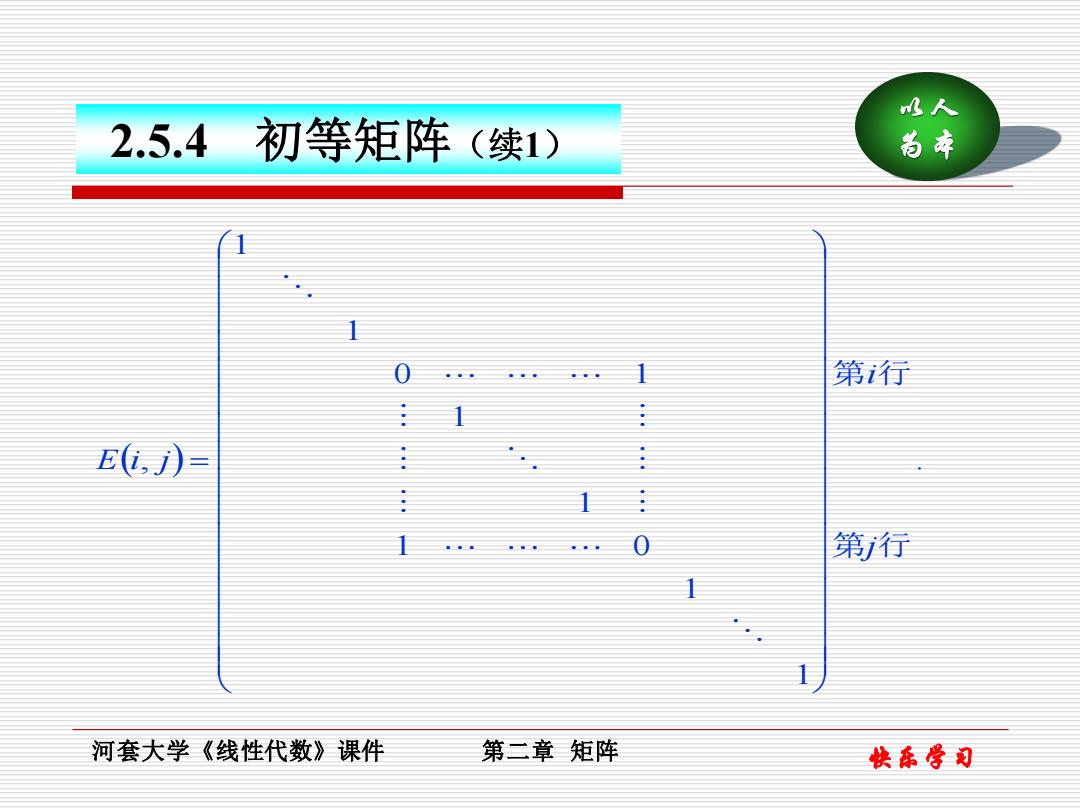
水人 2.5.4 初等矩阵（续1） 尚本 0 第行 E,) 1 0 第行 河套大学《线性代数》课件 第二章矩阵 快东学司

快乐学习 以人 为本 河套大学《线性代数》课件 第二章 矩阵 ( ) . 1 1 1 0 1 1 0 1 1 1 , 第 行 第 行 j i E i j                                     =                2.5.4 初等矩阵（续1）