河套学院（河套大学）：《线性代数》课程教学资源（PPT课件讲稿）第二章 矩阵 2.5 初等变换与初等矩阵

水人 2.5.4 初等矩阵（续2） 尚本 (2)以数入≠0乘单位矩阵的某行或某列.以数 入≠0乘单位阵E的第行G×入)得初等矩阵 E(2) 第行 河套大学《线性代数》课件 第二章矩阵 快东学司

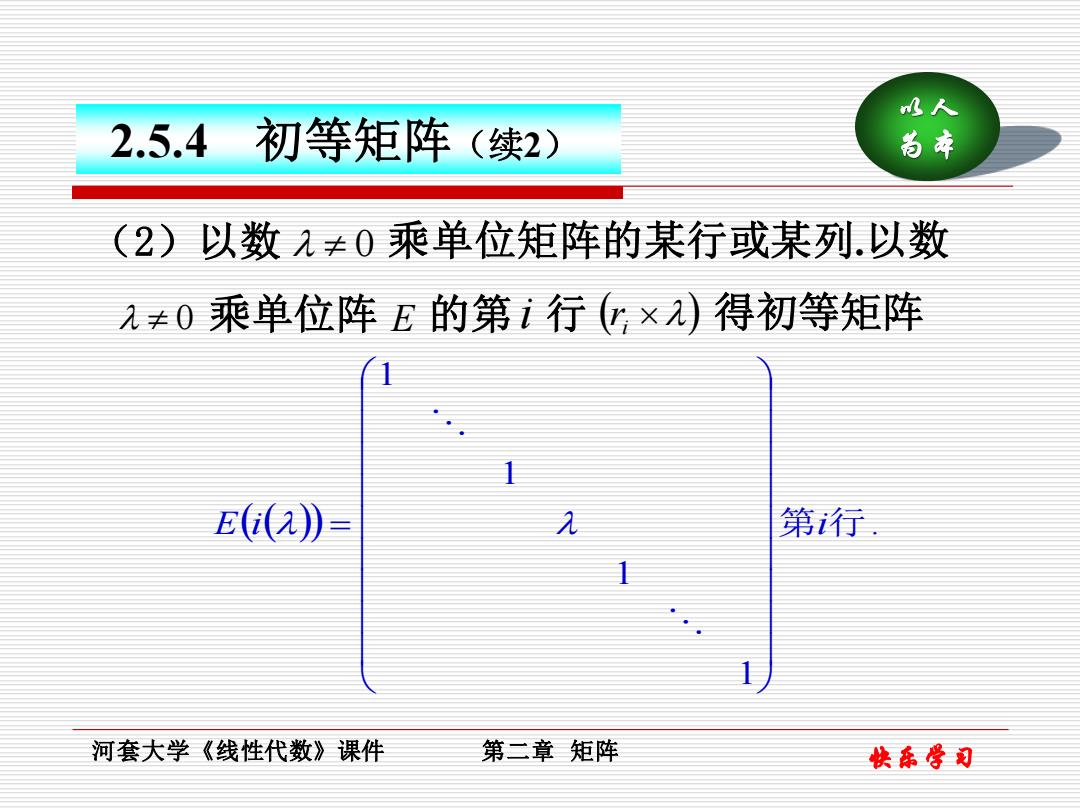
快乐学习 以人 为本 河套大学《线性代数》课件 第二章 矩阵 2.5.4 初等矩阵（续2） （2）以数   0 乘单位矩阵的某行或某列.以数   0 乘单位阵 E 的第 i 行 (  ) i r 得初等矩阵 ( ( )) . 1 1 1 1 E i 第i行                       =    

以人 2.5.4 初等矩阵（续3） 尚本 (3)以数乘单位矩阵的某行(（列)加到另 行（列)上，以入乘单位矩阵E的第行加到第 i行上+)或以乘E的第列加到第列上 c,+c)得初等矩阵 第行 E,(2) 第行 河套大学《线性代数》课件 第二章矩阵 快东学司

乘单位矩阵的某行（列）加到另一 快乐学习 以人 为本 河套大学《线性代数》课件 第二章 矩阵 2.5.4 初等矩阵（续3） （3）以数  行（列）上. 以  乘单位矩阵 E 的第 j 行加到第 i 行上 ( ) i j r + r 或以  乘 E 的第 i 列加到第 j 列上 ( ) j i c + c 得初等矩阵 ( ( )) 第 行 第 行 j i E i j                       = 1 1 1 1 ,      

水人 2.5.4 初等矩阵（续4） 尚本 下面以三阶矩阵为例，讨论初等矩阵左乘与 右乘矩阵对矩阵带来的变化 1213 412413 观察 00 2122 Q23 43 Q32 33 右边矩 010 阵多原 32433 a1 022 d23 矩阵的 12 4年 a13 412 吴秦 421Q22 a21 0l23 a22 431032 33 01 Q31Q33 2 和等矩阵左乘等价于雉阵进行行和等变换. 和等矩阵右乘号价于矩阵进行列初等变换 河套大学《线性代数》课件 第二章矩阵 快东学司

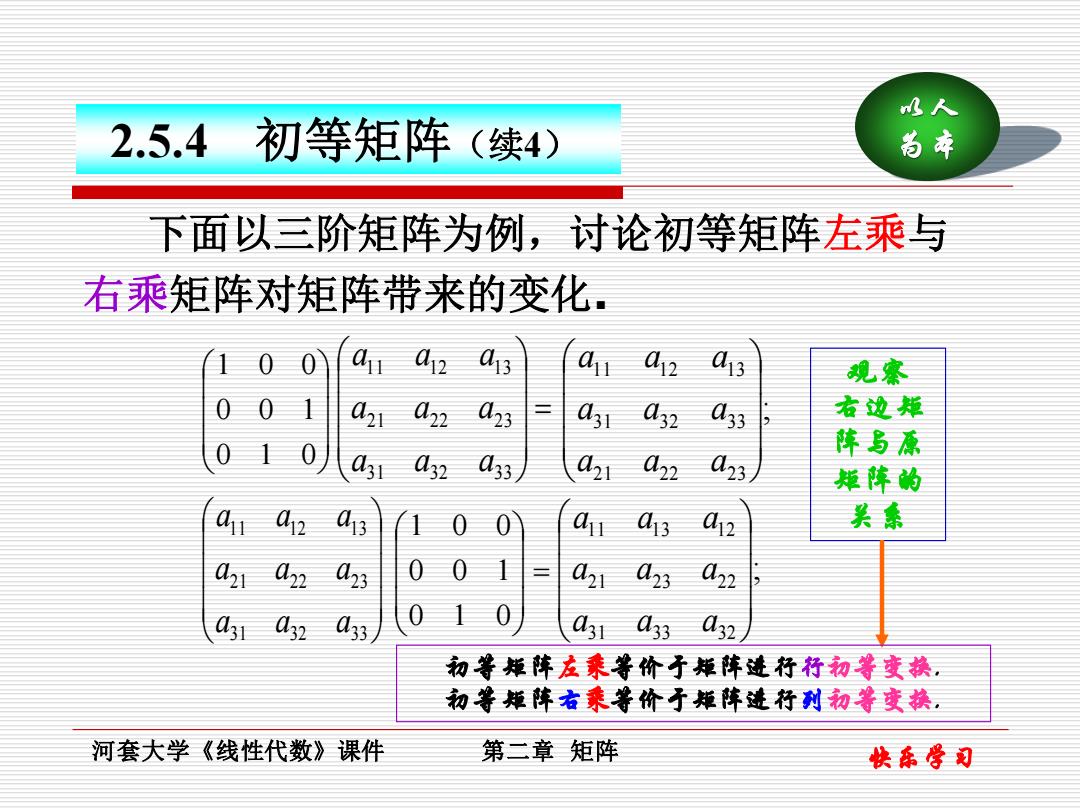
快乐学习 以人 为本 河套大学《线性代数》课件 第二章 矩阵 2.5.4 初等矩阵（续4） 下面以三阶矩阵为例，讨论初等矩阵左乘与 右乘矩阵对矩阵带来的变化.           0 1 0 0 0 1 1 0 0 =           31 32 33 21 22 23 11 12 13 a a a a a a a a a ; 21 22 23 31 32 33 11 12 13           a a a a a a a a a           31 32 33 21 22 23 11 12 13 a a a a a a a a a =           0 1 0 0 0 1 1 0 0 ; 31 33 32 21 23 22 11 13 12           a a a a a a a a a 观察 右边矩 阵与原 矩阵的 关系 初等矩阵左乘等价于矩阵进行行初等变换. 初等矩阵右乘等价于矩阵进行列初等变换