
■第三章随机过程 3.1随机过程的基本概念 3.2平稳随机过程 3.3高斯过程 3.4平稳随机过程通过线性系统 3.5窄带随机过程
1 第三章 随机过程 3.1 随机过程的基本概念 3.2 平稳随机过程 3.3 高斯过程 3.4 平稳随机过程通过线性系统 3.5 窄带随机过程

3.1随机过程的基本概念 随机过程是时间t的函数 ■在任意时刻观察,它是一个随机变量 ■随机过程是全部可能实现的总体 2
2 3.1 随机过程的基本概念 ◼ 随机过程是时间t的函数 ◼ 在任意时刻观察,它是一个随机变量 ◼ 随机过程是全部可能实现的总体
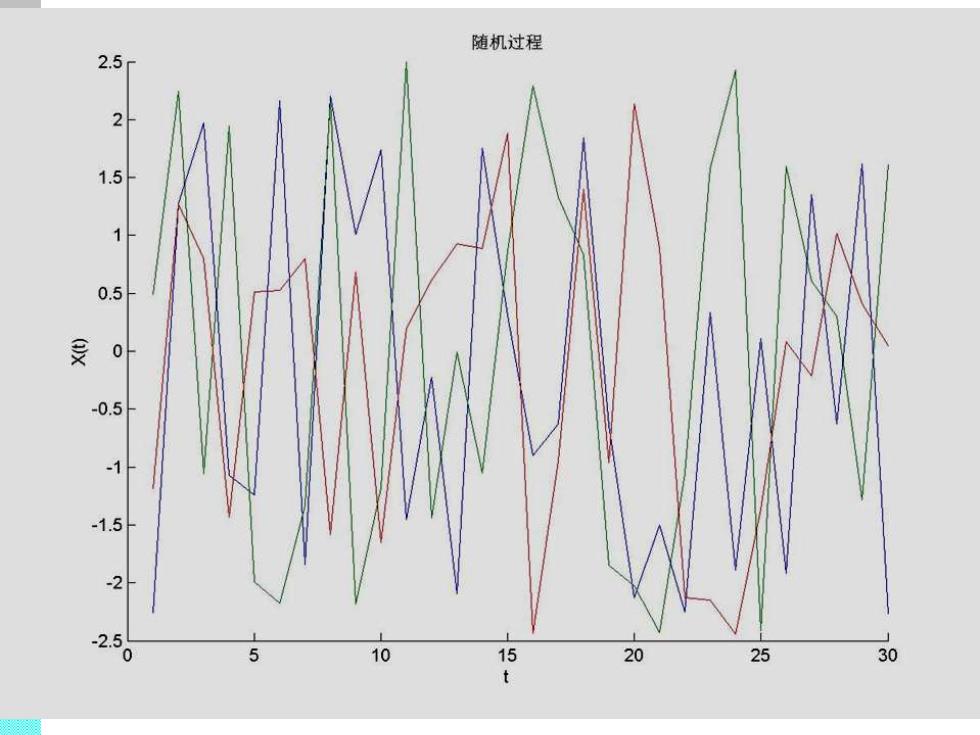
随机过程 2.5 1.5 0.5 0 0.5 15 .25 0 10 15 20 25 30
3

分布函数与概率密度: 设(t)表示一个随机过程,5(t)(t为任意时刻)是一 个随机变量。 F1(X1, t)=P{5(t上x1} 5(t)的一维分布函数 如果存在 aF(x,4) Ox =f(x1,t) 则称之为5(t)的一维概率密度函数
4 分布函数与概率密度: ◼ 设 表示一个随机过程, (t1为任意时刻)是一 个随机变量。 F1(x1,t1)=P{ ≤x1} 的一维分布函数 ◼ 如果存在 ◼ ◼ 则称之为 的一维概率密度函数 (t) ( ) 1 t ( ) 1 t (t) ( , ) ( , ) 1 1 1 1 1 1 1 f x t x F x t = (t)

5(t)的n维分布函数 F(x,x,.,x;t,1,.,t)=P{5()≤x5)≤x,.,5(t)≤x.} n维概率密度函数 aF.(x,x2,.x41)=f(,.X,4,.1) OxOx2.Oxn n越大,Fn,fn描述(t)的统计特性就越充分
5 的n维分布函数 n维概率密度函数 n越大,Fn,fn描述 的统计特性就越充分 n n n n n F (x , x , , x ;t ,t , ,t ) = P{ (t ) x , (t ) x , , (t ) x 1 2 1 2 1 1 2 2 n n n n n x x x F x x x t t t 1 2 1 2 1 2 ( , , ; , , , ) ( , , ; , , , ) n 1 2 n 1 2 n = f x x x t t t (t) (t)