
第5章数字基带传输系统 5.1典型例题 【例5-1】已知二元信息序列为0100110000100001100000000010,求DB3码,并画出 其波形图。 思路二元信息码中有4组4个连0码,第1、2组之间1码个数为奇数,第2、3组之 间及第3、4组之间1码的个数为偶数。据此,可以进行取代变换。取代变换之后再加符号 就得到HD3码。画波形图时应注意脉冲占空比为O.5,这是国际标准,不能随意画。 解取代变换后原二进制序列变为 010011000V1000V11B00VB00V010 加符号后得HDB,码。HDB,码及其波形图如图5-20所示。 皮形图 图5-20例5-1图 位的有4个连1和4个连0交替出现的序列,画出单极性非归零码、日 思路单极性非归零码、A码的编码规律比较简单。对DB码的编码规律比较熟悉后 即可直接由信息代码求出HDB码,并进而画出波形图。由于序列中4个连1和4个连0是 交替出现的,故相邻的4个连0码组之间1码的个数肯定是偶数个,因此DB码中的每个 取代节都应是BOOv。 解单极性非归零码、AM码、DB3码及其波形图如图521所示 信息代码 NRZ战形 AMm码1-11-100001-11-100001-11-10000 AMI被形 几LrLL HDB码 1-11-1B00V-11-11-B00-V1-11-1B00V waas nnhn 图5-21例5-2图 【例5-3】设随机二进制序列中的1码出现的概率为0.5,对应一个振幅等于1、宽度 等于码元间隔Ts的矩形脉冲,0码对应0电平。 (1)求其功率谱密度及功率,并画出功率谱曲线,求增零点带宽: (②)若1码对应一个占空比等于0.5的矩形脉冲,0码仍为0电平,重新回答(1)中的 问题 3)能否从上述两个信号中用滤波法直接提取码元同步所需的频率s=1/Ts的分量?若 能,给出该分量的功率: (④)分析离散谱£,的功率与1码概率P的关系
1 第 5 章 数字基带传输系统 5.1 典 型 例 题 【例 5-1】 已知二元信息序列为 0100110000100001100000000010,求 HDB3 码,并画出 其波形图。 思路 二元信息码中有 4 组 4 个连 0 码,第 1、2 组之间 1 码个数为奇数,第 2、3 组之 间及第 3、4 组之间 1 码的个数为偶数。据此,可以进行取代变换。取代变换之后再加符号 就得到 HDB3 码。画波形图时应注意脉冲占空比为 0.5,这是国际标准,不能随意画。 解 取代变换后原二进制序列变为 010011000V1000V11B00VB00V010 加符号后得 HDB3 码。HDB3 码及其波形图如图 5-20 所示。 图 5-20 例 5-1 图 【例 5-2】 有 4 个连 1 和 4 个连 0 交替出现的序列,画出单极性非归零码、AMI 码、HDB3 码所对应的波形图。 思路 单极性非归零码、AMI 码的编码规律比较简单。对 HDB3 码的编码规律比较熟悉后 即可直接由信息代码求出 HDB3 码,并进而画出波形图。由于序列中 4 个连 1 和 4 个连 0 是 交替出现的,故相邻的 4 个连 0 码组之间 1 码的个数肯定是偶数个,因此 HDB3 码中的每个 取代节都应是 B00V。 解 单极性非归零码、AMI 码、HDB3 码及其波形图如图 5-21 所示。 图 5-21 例 5-2 图 【例 5-3】 设随机二进制序列中的 1 码出现的概率为 0.5,对应一个振幅等于 1、宽度 等于码元间隔 Ts 的矩形脉冲,0 码对应 0 电平。 (1) 求其功率谱密度及功率,并画出功率谱曲线,求谱零点带宽; (2) 若 1 码对应一个占空比等于 0.5 的矩形脉冲,0 码仍为 0 电平,重新回答(1)中的 问题; (3) 能否从上述两个信号中用滤波法直接提取码元同步所需的频率 fs=1/Ts 的分量?若 能,给出该分量的功率; (4) 分析离散谱 fs 的功率与 1 码概率 P 的关系

思路第一个信号为单极性非归零码,第二个信号为占空比等于0.5的单极性归零码, 它们的基本波形为DT.(t)和D0.5T.()。这两个信号都是相同波形随机序列,可用式(5-3) 求其功率谱。若功率谱中含有=1/的离散语,则可用滤波法直接提取频率为.的他 定时信号,否则不能。 傅氏变换对 D.()-:Sa()=sn/2 0t/2 是本课程中常用公式,此题中t=.或t=0.5T。 解(1)P=0.5,al,a-0 G(f)=T,Sa(fT,)=T,Sa(f/f,) 代入式(5-3)得 P.(f)=f.x0.5X0.5XT*Sa(n f/f.) .'xTSa'(f./)5(f-mf.) =0.25T.Sa(rf/f.)+0.25∑Sa(m)6(f-mf.) 由于 sin(mx)=0 所以 Sa(m)=0 故 P.(f)=0.25t.Sa(mf/) 功率谱密度曲线如图5-22所示。 一0 图5-22例5-3图1 由图5-22可知,谱零点带宽为B.=f。 信号功率为 .s( 0.25f.jrs(/f 根据帕塞瓦尔定理 ar.r (2)P=0.5 G(f)=0.5t.Sa(0.5πfT,)=0.5t.5a(0.5mf/f,) P.(f)=0.0625T.Sa(0.5f/f.)
2 思路 第一个信号为单极性非归零码,第二个信号为占空比等于 0.5 的单极性归零码, 它们的基本波形为 DTs(t)和 D0.5Ts(t)。这两个信号都是相同波形随机序列,可用式(5-3) 求其功率谱。若功率谱中含有 fs=1/Ts 的离散谱,则可用滤波法直接提取频率为 fs=1/Ts 的位 定时信号,否则不能。 傅氏变换对 Dτ(t)←→τSa ) 2 ( =τ / 2 sin / 2 是本课程中常用公式,此题中τ=Ts 或τ=0.5Ts。 解 (1) P=0.5,a1=1,a2=0 G(f)=TsSa(πfTs)=TsSa(πf/fs) 代入式(5-3)得 Ps(f)=fs×0.5×0.5×T 2 sSa2 (πf/fs) +f2 s m=− 0.52×T 2 sSa2 (mπfs/fs)δ(f-mfs) =0.25TsSa2 (πf/fs)+0.25 m=− Sa2 (mπ)δ(f-mfs) 由于 sin(mπ)=0 所以 Sa(mπ)=0 故 Ps(f)=0.25TsSa2 (πf/fs) 功率谱密度曲线如图 5-22 所示。 图 5-22 例 5-3 图 1 由图 5-22 可知,谱零点带宽为 Bs=fs。 信号功率为 S= − Ps(f)df=0.25 − TsSa2 (πf/fs)df =0.25fs − T 2 sSa2 (πf/fs)df 根据帕塞瓦尔定理 − T 2 sSa2 (πf/fs)df= − |G(f)|2 df= − D 2 Ts(t)dt=T2 s 得 (2) P=0.5 G(f)=0.5TsSa(0.5πfTs)=0.5TsSa(0.5πf/fs) Ps(f)=0.0625TsSa2 (0.5πf/fs)
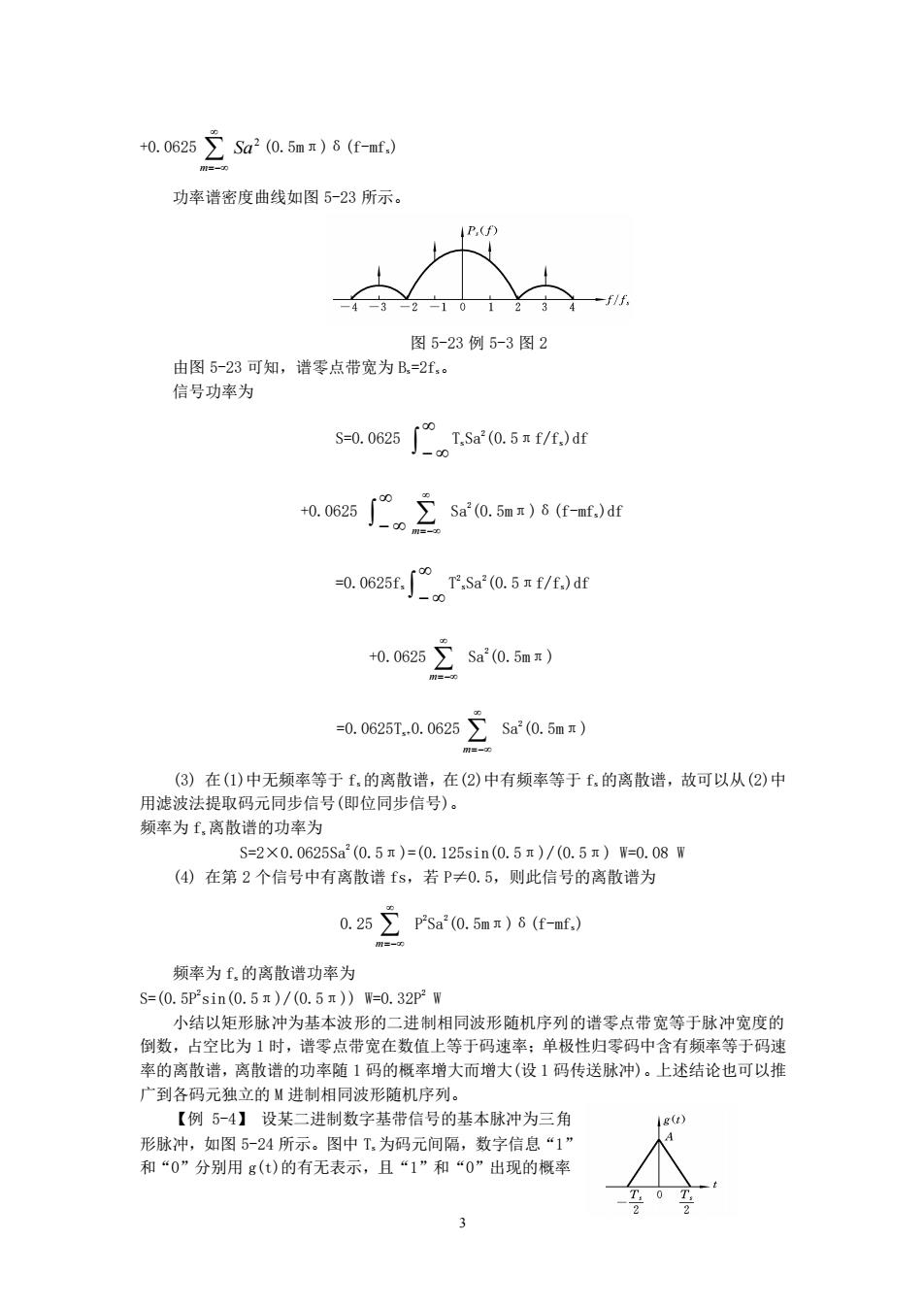
+0.0625∑Sa2(0.5m)6(f-mf,) 功率谱密度曲线如图5-23所示。 RCD 图5-23例5-3图2 由图5-23可知,谱零点带宽为B=2f,。 信号功率为 -.02( aoas三aa6 n0w5trsa.5a/iDdr +0.0625Sa2(0.5mm) -0.06251.06255a.5m (③)在(1)中无频率等于£,的离散谱,在(2)中有频率等于£,的离散谱,故可以从(2)中 用滤波法提取码元同步信号(即位同步信号)。 频率为,离散谱的功率为 S=2×0.0625Sa'(0.5π)=(0.125sin(0.5r)/(0.5r)f=0.08T (4)在第2个信号中有离散谱fs,若P≠0.5,则此信号的离散谱为 0.25∑psa2(0.5mm)6(f-mf,) 频率为£的离散谱功率为 S=(0.5Psin(0.5)/(0.5))W=0.32pW 小结以矩形脉冲为基本波形的二进制相同波形随机序列的谱零点带宽等于脉冲宽度的 倒数,占空比为1时,谱零点带宽在数值上等于码速率:单极性归零码中含有频率等于码速 率的离散谱,离散谱的功率随1码的概率增大而增大(设1码传送脉冲)。上述结论也可以推 广到各码元独立的M进制相同波形随机序列。 【例5-4】设某二进制数字基带信号的基本脉冲为三角 g() 形脉冲,如图5-24所示。图中T,为码元间隔,数字信息“1” 和“0”分别用g(t)的有无表示,且“1”和“0”出现的概率
3 +0.0625 2 Sa m =− (0.5mπ)δ(f-mfs) 功率谱密度曲线如图 5-23 所示。 图 5-23 例 5-3 图 2 由图 5-23 可知,谱零点带宽为 Bs=2fs。 信号功率为 S=0.0625 − TsSa2 (0.5πf/fs)df +0.0625 − m=− Sa2 (0.5mπ)δ(f-mfs)df =0.0625fs − T 2 sSa2 (0.5πf/fs)df +0.0625 m=− Sa2 (0.5mπ) =0.0625Ts+0.0625 m=− Sa2 (0.5mπ) (3) 在(1)中无频率等于 fs 的离散谱,在(2)中有频率等于 fs 的离散谱,故可以从(2)中 用滤波法提取码元同步信号(即位同步信号)。 频率为 fs 离散谱的功率为 S=2×0.0625Sa2 (0.5π)=(0.125sin(0.5π)/(0.5π) W=0.08 W (4) 在第 2 个信号中有离散谱 fs,若 P≠0.5,则此信号的离散谱为 0.25 m=− P 2 Sa2 (0.5mπ)δ(f-mfs) 频率为 fs 的离散谱功率为 S=(0.5P2 sin(0.5π)/(0.5π)) W=0.32P2 W 小结以矩形脉冲为基本波形的二进制相同波形随机序列的谱零点带宽等于脉冲宽度的 倒数,占空比为 1 时,谱零点带宽在数值上等于码速率;单极性归零码中含有频率等于码速 率的离散谱,离散谱的功率随 1 码的概率增大而增大(设 1 码传送脉冲)。上述结论也可以推 广到各码元独立的 M 进制相同波形随机序列。 【例 5-4】 设某二进制数字基带信号的基本脉冲为三角 形脉冲,如图 5-24 所示。图中 Ts 为码元间隔,数字信息“1” 和“0”分别用 g(t)的有无表示,且“1”和“0”出现的概率

相等。 图5-24例5-4图 (1)求该数字基带信号的功率谱密度: (2)能否用滤被法从该数字基带信号中提取码元同步所需的频率=1/T,的分量?若能, 试计算该分量的功率。 思路将底部宽度为t、高度为1的三角形时域函数表示为△t(),傅氏变换对为 4.0-一Ia=5aor14 @r/4 据此式可求得本题中g(t)所对应的G(f),再由式(5-3)即可求解。 解(1 P=0.5,a=l,a=0 2 Rm=f-刊aac0f2laa-刊aeaD5md 4 4 4 -悟立学W 16 (2)频率f.=1/1,离散谱分量为 专iU-#60-0 所以可以用滤波法从该数字基带信号中提取码元同步所需要的频率£.=1/几,的分量,该分量 的功率为 【例5-5】某基带系统的频率特性是截止频率为1z、幅度为1的理想低通滤波器 (1)试根据系统无码间串扰的时域条件求此基带系统无码间串扰的码速率。 (2)设此系统传输信息速率为3Ms,能否无码间串扰? 思路此题需求系统的冲激响应。系统的频率特性是一个幅度为1、宽度为⊙。=4π×10 rad/s的门函数(双边频率特性)Do(u),根据傅氏变换的对称性可得 D,(o)-一%a()-2x10rsa2r×10rt) 2π 2 无码间串扰的时域条件为 C,k=0 MkI,)=0,k0 式中,工,为码元间隔。所以,根据冲激响应波形就可确定此系统无码间串扰的码速率。 设进制数为任意值,根据信息速率与码速率之间的关系求3Mbs所对应的码速率,从 而判断传输3Mbps信号有无码间串扰。 4
4 相等。 图 5-24 例 5-4 图 (1) 求该数字基带信号的功率谱密度; (2) 能否用滤波法从该数字基带信号中提取码元同步所需的频率 fs=1/Ts 的分量?若能, 试计算该分量的功率。 思路 将底部宽度为τ、高度为 1 的三角形时域函数表示为Δτ(t),傅氏变换对为 Δτ(t)←→ 2 2 ] / 4 sin / 4 [ 2 )] 4 [ ( 2 Sa = 据此式可求得本题中 g(t)所对应的 G(f),再由式(5-3)即可求解。 解 (1) P=0.5,a1=1,a2=0 G(f)= ) 2 ( 2 s 2 s fT Sa AT Ps(f)=fsP(1-P)(a1-a2) 2 G 2 (f)+f2 s m=− |Pa1+(1-P)a2| 2 G(mfs)δ(f-mfs) = 4 s f · ) 2 ( 4 4 2 2 s s fT Sa A T + ) 2 ( 4 4 4 2 2 2 s s m s fT Sa f A T =− δ(f-mfs) ) ( ) 2 ( 16 ) 2 ( 16 4 2 2 2 s m s s f mf m Sa fT A Sa A T = + − =− (2) 频率 fs=1/Ts 离散谱分量为 ( ) 0 2 ) ( ) 2 ( 8 4 2 4 2 − s = f − f s A Sa f f A 所以可以用滤波法从该数字基带信号中提取码元同步所需要的频率 fs=1/Ts 的分量,该分量 的功率为 【例 5-5】 某基带系统的频率特性是截止频率为 1 MHz、幅度为 1 的理想低通滤波器。 (1) 试根据系统无码间串扰的时域条件求此基带系统无码间串扰的码速率。 (2) 设此系统传输信息速率为 3 Mbps,能否无码间串扰? 思路 此题需求系统的冲激响应。系统的频率特性是一个幅度为 1、宽度为ω0=4π×106 rad/s 的门函数(双边频率特性)Dω0(ω),根据傅氏变换的对称性可得 Dω0(ω)←→ ) 2 ( 2 0 0 t Sa =2×106 Sa(2π×106 t) 无码间串扰的时域条件为 = = 0, 0 , 0 ( ) k C k h kTs 式中,Ts 为码元间隔。所以,根据冲激响应波形就可确定此系统无码间串扰的码速率。 设进制数为任意值,根据信息速率与码速率之间的关系求 3 Mbps 所对应的码速率,从 而判断传输 3 Mbps 信号有无码间串扰

解(1)h(t)=2×10Sa(2πX10t) 波形如图525所示。由图可知,当T=0.54s/k(k为正整数)时无码间串扰,即此系 统无码间串扰的码速率为 h(r) 图5-25例5-5图 (2)设传输独立等概的M进制信号,则 g:Mm) 3 32 log2 Mk 8=8(n=L,2,.) 即当采用8进制信号时,码速率R(QB),可以满足无码间串扰 n H(oo 条件 例5-6】设某基带传输系统具有图5-26所示的三角形传输函数: ()当R=。/π时,用奈奎斯特准则验证该系统能否实现无码间 0 串扰传输? 图5-26例5-6图1 (②)求该系统接收滤波器输出基本脉冲的时间表达式,并用此来说明(1)中的结论 思路因R=0/T,即R=2f,所以式(5-5)或式(5-6)中的£,=2f。也可将式(5-5)或 式(5-6)表示为角频率的形式 ∑H(unwJ-clo≤g 或∑H(on心)-C。为任意位 若用此两式,则对于此题给定的条件,有 0,=200 根据傅氏变换的对称性,可得 由此式可求得本题所给系统的接收滤波器输出基本脉冲时间表达式,再根据码速率决定 抽样时刻,从而决定有无码间串扰。 解(1)方法一 将H(w)在频率轴上以2u。为间隔切开,由于H(u)的频率范围为(←u,。),故切开、 平移、选加后仍为H(ω),在|w|《o范围内(u)不为常数,故系统有码间串扰
5 解 (1) h(t)=2×106 Sa(2π×106 t) 波形如图 5-25 所示。由图可知,当 Ts=0.5 μs/k(k 为正整数)时无码间串扰,即此系 统无码间串扰的码速率为 图 5-25 例 5-5 图 (2) 设传输独立等概的 M 进制信号,则 RB= log 2 M 3 (MBd) 令 log 2 M 3 = k 2 得 M= k 2 8 =8n (n=1,2,.) 即当采用 8 n 进制信号时,码速率 RB= n 1 (MBd),可以满足无码间串扰 条件。 【例 5-6】设某基带传输系统具有图 5-26 所示的三角形传输函数: (1) 当 RB=ω0/π时,用奈奎斯特准则验证该系统能否实现无码间 串扰传输? 图 5-26 例 5-6 图 1 (2) 求该系统接收滤波器输出基本脉冲的时间表达式,并用此来说明(1)中的结论。 思路 因 RB=ω0/π,即 RB=2f0,所以式(5-5)或式(5-6)中的 fs=2f0。也可将式(5-5)或 式(5-6)表示为角频率的形式 n=− H(ω+nωs)=C,|ω|≤ 2 s 或 n=− H(ω+nωs)=C,ω为任意值 若用此两式,则对于此题给定的条件,有 s = 20 根据傅氏变换的对称性,可得 ΔΩ(ω)←→ 2 2 ] / 4 sin / 4 [ 4 )] 4 [ ( 4 t t t Sa = 由此式可求得本题所给系统的接收滤波器输出基本脉冲时间表达式,再根据码速率决定 抽样时刻,从而决定有无码间串扰。 解 (1) 方法一 将 H(ω)在频率轴上以 2ω0 为间隔切开,由于 H(ω)的频率范围为(-ω0,ω0),故切开、 平移、迭加后仍为 H(ω),在|ω|<ω0 范围内 H(ω)不为常数,故系统有码间串扰