
第7章模拟信号的数字传输 7.1典型例题 【例7-1】已知信号m(t)=10cos(20It)cos(200πt),抽样频*E,=250z。 (1)求已抽样信号m()的频谱: (2)要求无失直恢复m(t),试求对m(t)采用的低頫滤波器的截止师率: 3)试求无失真恢复m()情况下的最低抽样频率 解(①)m()=5c0s(220)+5c0s(180rt M(f)=5I[6(f+110)+6(f-110)+6(f+90)+8(f-90)] L(f)=f,∑M(f+nf,)=1250元∑M(f+250m) m(t)的频谱如图7-16所示。 IM.( 图7-16例7-1图 (②)低通滤波器的截止频率为110H2。 (③)根据低通信号抽样定理,最低抽样频率f.=110×2Hz=220Hz。 【例7-2】已知一低通信号m(t)的频谱M(E)为 200 0,其它 (1)假设以300z的速率对m(t)进行理想抽样,试画出已抽样信号m,(t)的频谱草图: (2)若用f.=400Hz的速率抽样,重做上题。 解()■()的频谱如图7-17(a)所示,画()的频谱M()如图7-17)所示。 (2)f.=400z时,m(t)的频谱如图7-17(c)所示
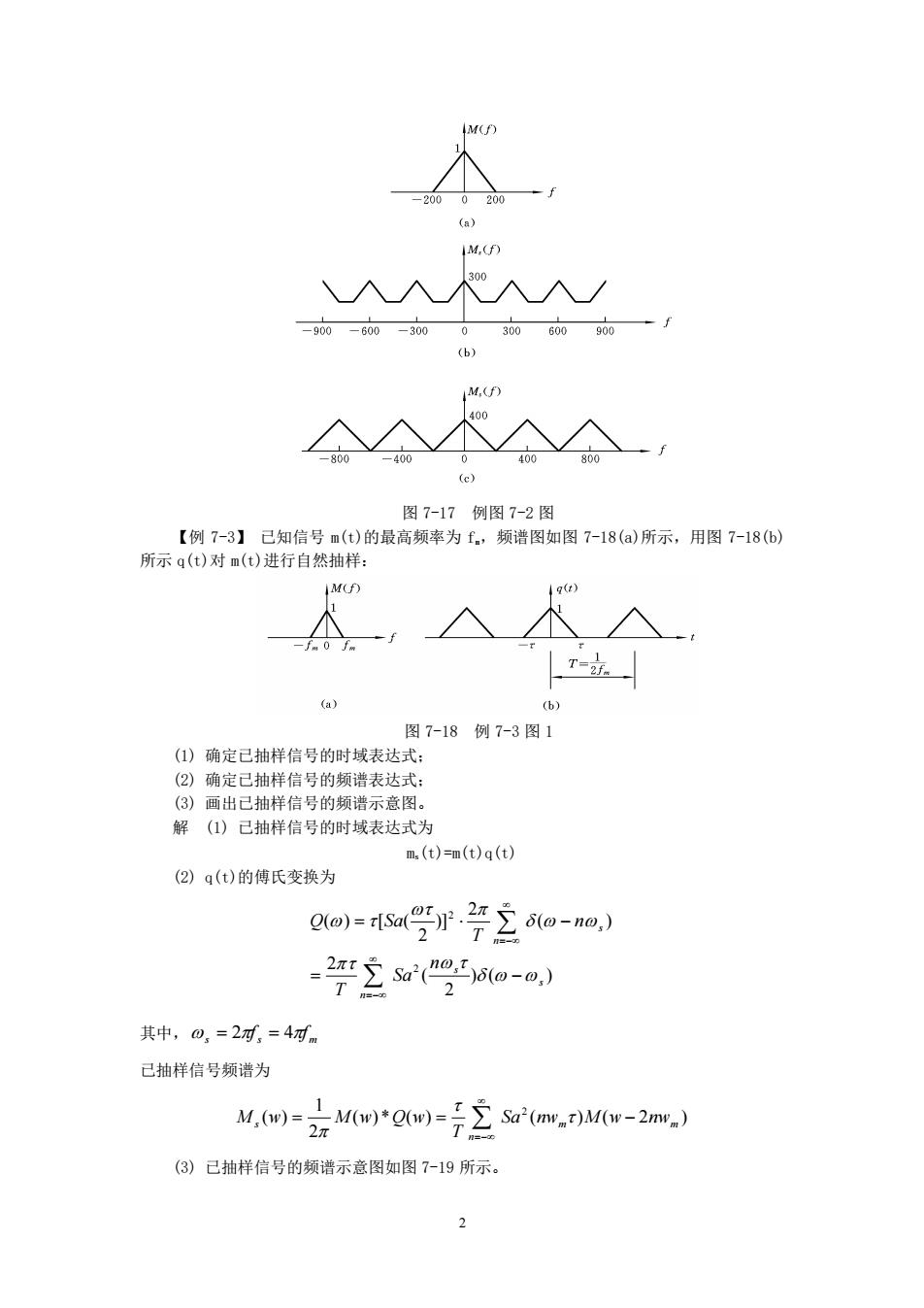
1 第 7 章 模拟信号的数字传输 7.1 典 型 例 题 【例 7-1】 已知信号 m(t)=10cos(20πt)cos(200πt),抽样频率 fs=250 Hz。 (1) 求已抽样信号 ms(t)的频谱; (2) 要求无失真恢复 m(t),试求对 ms(t)采用的低频滤波器的截止频率; (3) 试求无失真恢复 m(t)情况下的最低抽样频率 fs。 解 (1) m(t)=5cos(220πt)+5cos(180πt) M(f)=5π[δ(f+110)+δ(f-110)+δ(f+90)+δ(f-90)] Ms(f)=fs n=− M(f+nfs)=1250π n=− M(f+250n) ms(t)的频谱如图 7-16 所示。 图 7-16 例 7-1 图 (2) 低通滤波器的截止频率为 110 Hz。 (3) 根据低通信号抽样定理,最低抽样频率 fs=110×2 Hz=220 Hz。 【例 7-2】 已知一低通信号 m(t)的频谱 M(f)为 M(f)= − 0,其它 ,| | 200 200 | | 1 f Hz f (1) 假设以 300 Hz 的速率对 m(t)进行理想抽样,试画出已抽样信号 ms(t)的频谱草图; (2) 若用 fs=400 Hz 的速率抽样,重做上题。 解 (1) m(t)的频谱如图 7-17(a)所示,ms(t)的频谱 Ms(f)如图 7-17(b)所示。 (2) fs=400 Hz 时,ms(t)的频谱如图 7-17(c)所示
M.( -600-3000 30600900 图7-17例图7-2图 【例7-3】己知信号m()的最高频率为f,频谱图如图7-18(a)所示,用图7-18(b) 所示q(t)对()进行自然抽样 9() T=. w 图7-18例7-3图1 ()确定己抽样信号的时域表达式: (2)确定己抽样信号的频谐表达式: ③)画出己抽样信号的缬谐示意图。 解()已抽样信号的时域表达式为 m.(t)=m(t)q(t) (2)q(t)的傅氏变换为 go)=a(r2立a-nm,) 22%5a-a) 其中,0,=2列,=4河 己抽样信号频谱为 M.()()()(m)M(w-2m) (3)已抽样信号的频谱示意图如图7-19所示
2 图 7-17 例图 7-2 图 【例 7-3】 已知信号 m(t)的最高频率为 fm,频谱图如图 7-18(a)所示,用图 7-18(b) 所示 q(t)对 m(t)进行自然抽样: 图 7-18 例 7-3 图 1 (1) 确定已抽样信号的时域表达式; (2) 确定已抽样信号的频谱表达式; (3) 画出已抽样信号的频谱示意图。 解 (1) 已抽样信号的时域表达式为 ms(t)=m(t)q(t) (2) q(t)的傅氏变换为 ) ( ) 2 ( 2 ( ) 2 )] 2 ( ) [ ( 2 2 s s n s n n Sa T n T Q Sa = − = − =− =− 其中, s s m = 2f = 4f 已抽样信号频谱为 ( ) * ( ) ( ) ( 2 ) 2 1 ( ) 2 m m n s Sa nw M w nw T M w = M w Q w = − =− (3) 已抽样信号的频谱示意图如图 7-19 所示

S02(xr) 图7-19例7-3图2(设=5.) 【例7-4】设m()频谱如图7一18(a)所示,用图7-18)所示q()的单个脉冲对m() 进行瞬时抽样: (1)确定已抽样信号的时域表达式: (②)确定已抽样信号的频域表达式: (③)画出己抽样信号的频谱示意图。 解(Q①)瞬时抽样的原理框图如图7-5(a)所示,已抽样信号的时域表达式为 (2)q(t)的频谱为 9(o)=r5r(9 所以m,()的频谱为 L(o)=号[立Ma+a小q(o)=号s(7)三(o+2) (3)血()的频谱图如图7-20所示。 M.( Sa( 人人人人入 -4f-2f0 2f 图7-20例7-4图 图7-21例7-5例图1 【例7-5】已知模拟信号抽样值的概率密度p(x)如图7-21所示。 ()如果按4电平进行均匀量化,试计算信号与量化噪声功率比: (②)如果按8电平进行均匀量化,试确定量化间隔和量化电平: (③)如果按8电平进行非均匀量化,试确定能使量化信号电平等概的非均匀量化区间, 并画出压缩特性 解(1)分层电平为 x1=-1,x=-0.5,x=0,x=0.5,xg=1 量化电平为 y=-0.75,yg=-0.25,y=0.25,y=0.75 信号功率为 s小布e2时05-团r号 6
3 图 7-19 例 7-3 图 2(设 m 5 f 1 = ) 【例 7-4】 设 m(t)频谱如图 7—18(a)所示,用图 7-18(b)所示 q(t)的单个脉冲对 m(t) 进行瞬时抽样: (1) 确定已抽样信号的时域表达式; (2) 确定已抽样信号的频域表达式; (3) 画出已抽样信号的频谱示意图。 解 (1) 瞬时抽样的原理框图如图 7-5(a)所示,已抽样信号的时域表达式为 ms(t)=[ n=− m(t)δ(t+nT)]*q(t) (2) q(t)的频谱为 Q(ω)=τSa2 ) 2 ( w 所以 ms(t)的频谱为 Ms(ω)= T 1 [ n=− M(ω+2nωm)]·Q(ω)= T Sa2 ) 2 ( w n=− (ω+2nωm) (3) ms(t)的频谱图如图 7-20 所示。 图 7-20 例 7-4 图 图 7-21 例 7-5 例图 1 【例 7-5】 已知模拟信号抽样值的概率密度 p(x)如图 7-21 所示。 (1) 如果按 4 电平进行均匀量化,试计算信号与量化噪声功率比; (2) 如果按 8 电平进行均匀量化,试确定量化间隔和量化电平; (3) 如果按 8 电平进行非均匀量化,试确定能使量化信号电平等概的非均匀量化区间, 并画出压缩特性。 解 (1) 分层电平为 x1=-1, x2=-0.5,x3=0,x4=0.5,x5=1 量化电平为 y1=-0.75, y2=-0.25, y3=0.25, y4=0.75 信号功率为 S= −1 1 x 2 p(x)dx=2 0.5 1 x 2 (1-x)dx= 6 1
量化噪声功率为 信号与量化噪声功率比为 SNR.=S/N.=8 (②)量化间隔为 △=2/8=1/4 量化电平分别为 -7/8,-5/8,-3/8,-1/8,1/8,3/8,5/8,7/8 (3)设分层电平依次为-1,X,x,-x,0,x,x,1,依题意 可得下列方程 8 x-专 解之,得 2aa25n 2 量化电平为相邻分层电平的平均值,依次为-0.75,0.40,-0.21,-0.07,0.07 0.21,0.40,0.75 压缩特性曲线如图7-22所示。 0.75 0.40 15 .21 .130.290.5 -0.40 7 图7-22例7-5图2 【例7-6】设正弦信号动态范围为45dB,量化信噪比不低于26dB,求线性PCW的编 码位 解最大量化信噪比为 [SNR(26+45)dB=71 dB 由式(7-10)得 [SNR1=1.77+6N≥71
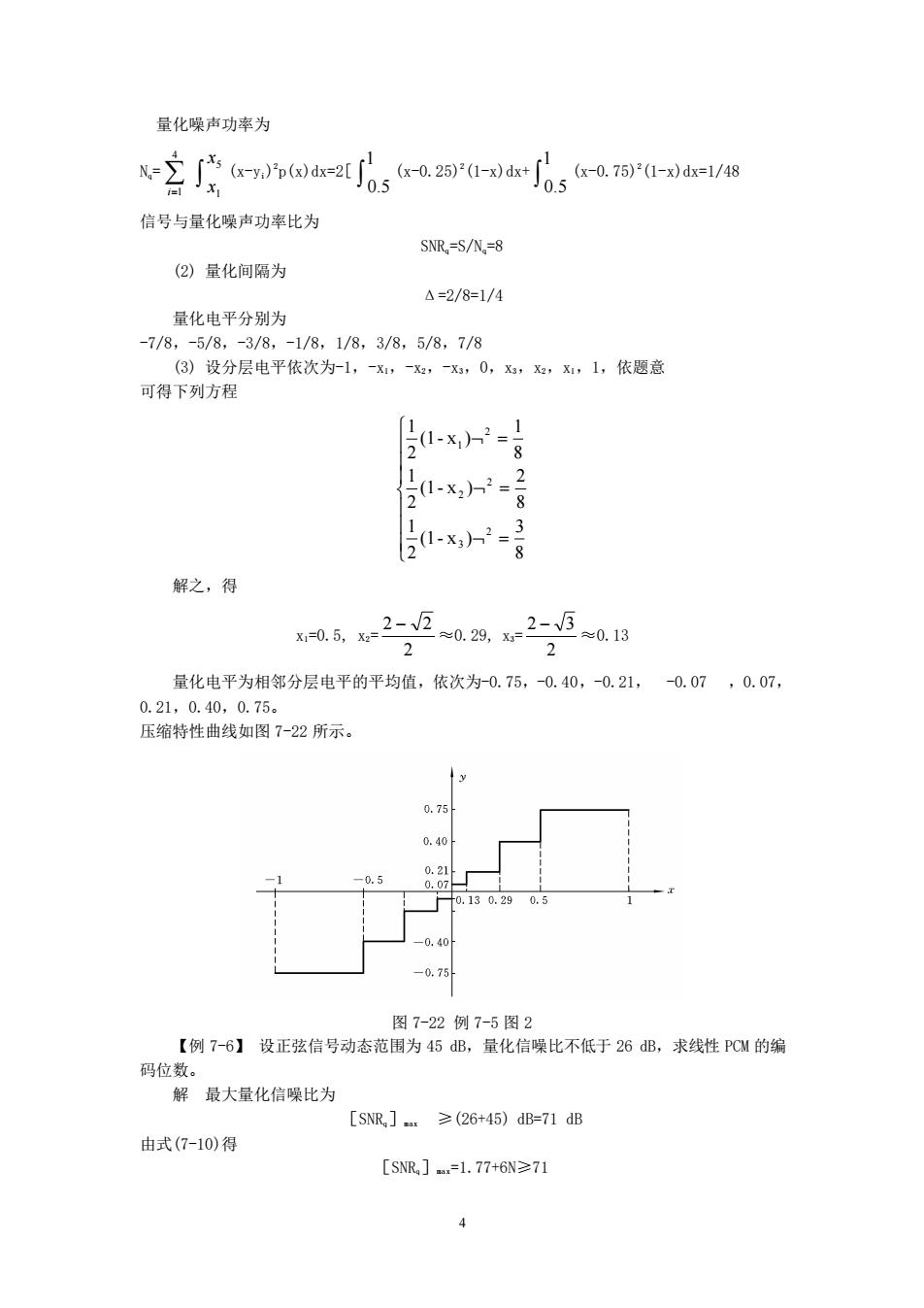
4 量化噪声功率为 Nq= = 1 5 4 1 x x i (x-yi) 2 p(x)dx=2[ 0.5 1 (x-0.25)2 (1-x)dx+ 0.5 1 (x-0.75)2 (1-x)dx=1/48 信号与量化噪声功率比为 SNRq=S/Nq=8 (2) 量化间隔为 Δ=2/8=1/4 量化电平分别为 -7/8,-5/8,-3/8,-1/8,1/8,3/8,5/8,7/8 (3) 设分层电平依次为-1,-x1,-x2,-x3,0,x3,x2,x1,1,依题意 可得下列方程 = = = 8 3 (1- x ) 2 1 8 2 (1- x ) 2 1 8 1 (1- x ) 2 1 2 3 2 2 2 1 解之,得 x1=0.5, x2= 2 2 − 2 ≈0.29, x3= 2 2 − 3 ≈0.13 量化电平为相邻分层电平的平均值,依次为-0.75,-0.40,-0.21, -0.07 ,0.07, 0.21,0.40,0.75。 压缩特性曲线如图 7-22 所示。 图 7-22 例 7-5 图 2 【例 7-6】 设正弦信号动态范围为 45 dB,量化信噪比不低于 26 dB,求线性 PCM 的编 码位数。 解 最大量化信噪比为 [SNRq]max ≥(26+45) dB=71 dB 由式(7-10)得 [SNRq]max=1.77+6N≥71

N>12 即线性PCM的编码位数至少为12才能满足对量化信噪比的要求。 【例7-7】输入信号抽样值x为630个最小量化单位,求A律P0M码、译码输出和量 化误 解(1)先采用逐位比较法确定PCW码组 因为x>0,所以C=1 因为x》128,所以C=1,处于第5一8段落内 因为x0512,所以C= ,处于第7或第8段落内 因为x<1024 所以C 于第7段落 (人工编码时,上述第2、3、4步可以合在一起:因为512(x<1024,所以C:CC=110) 再逐位确定段内码 -512=118 因为118<8×32-256,所以C=0 因为118<4×32=128 所以C 因为118>2×32=64,所以C=1 因为118-64=54>1×32,所以C。=1 即PCM码组为11100011,此码组对应的量化值为512+64+32=608,量化误差为 ©,=630-608=22。编码器的量化误差可大于量化间隔的一半,不是最佳编码器。 (2)译码输出及量化误差 译码输出为编码器的量化电平加上编码器输入信号所处段落的量化间隔的一半,即为 608+32/2=624 译码器输出的量化误差为 630-624=6 讨论译码器首先将对数PCM转换为线性PCM,再进行数模转换。若将A律PCM码11IOOO1I 转换为12位线性码(仅称自然码)101001100000(第1位为符号位) 则译码结果为608,量 化结果不是最佳的(量化误差大于量化间隔的一半)。实际使用的译码器是将A律PCM码按照 表7-2转换为13位线性PC码,再进行数模转换,从而使译码输出(即量化电平)处于量化 区间的中间,实现最佳量化。 出题A律PCy码11100011对应的13位线性PC为1010011100000(第1位为符号位) 对应的十进制数为608×2+32=1248,相当于将编码器的输出电平增大1倍再加上该段落的 量化电平,为了与抽样值进行比较,认为译码吗输出为608+32/2=624。 【例7-8】设简单增量调制器输入的正弦信号频率为3.4kz、幅度为1V,若抽样频 密=32kH2,求量阶0 解正弦信号最大斜率为 Au=1×2×3.4×10 为使△M不过载,必须满足 Au≤0f 由此得 0≥4=20x34x10y=0.6N 32×103 【例7-9】对10路带宽均为300~3400z的模拟信号进行PCM时分复用传输。抽样 速率为8000Hz,抽样后进行8级量化,并编为自然二进制码,码元波形是宽度为ī的矩形 脉冲,且占空比为1。试求传输此时分复用CM信号所需的最小带宽(设码流中无顿同步码 5
5 N≥12 即线性 PCM 的编码位数至少为 12 才能满足对量化信噪比的要求。 【例 7-7】 输入信号抽样值 x 为 630 个最小量化单位,求 A 律 PCM 码、译码输出和量 化误差。 解 (1) 先采用逐位比较法确定 PCM 码组 因为 x>0,所以 C1=1 因为 x>128,所以 C2=1,处于第 5~8 段落内 因为 x>512,所以 C3=1,处于第 7 或第 8 段落内 因为 x<1024,所以 C4=0,处于第 7 段落 (人工编码时,上述第 2、3、4 步可以合在一起:因为 512<x<1024,所以 C2C3C4=110) 再逐位确定段内码 x-512=118 因为 118<8×32=256,所以 C5=0 因为 118<4×32=128,所以 C6=0 因为 118>2×32=64,所以 C7=1 因为 118-64=54>1×32,所以 C8=1 即 PCM 码组为 11100011,此码组对应的量化值为 512+64+32=608,量化误差为 eq=630-608=22。编码器的量化误差可大于量化间隔的一半,不是最佳编码器。 (2) 译码输出及量化误差 译码输出为编码器的量化电平加上编码器输入信号所处段落的量化间隔的一半,即为 608+32/2=624 译码器输出的量化误差为 630-624=6 讨论 译码器首先将对数PCM转换为线性PCM,再进行数模转换。若将A律PCM码11100011 转换为 12 位线性码(又称自然码)101001100000(第 1 位为符号位),则译码结果为 608,量 化结果不是最佳的(量化误差大于量化间隔的一半)。实际使用的译码器是将 A 律 PCM 码按照 表 7-2 转换为 13 位线性 PCM 码,再进行数模转换,从而使译码输出(即量化电平)处于量化 区间的中间,实现最佳量化。 此题 A 律 PCM 码 11100011 对应的 13 位线性 PCM 码为 1010011100000(第 1 位为符号位), 对应的十进制数为 608×2+32=1248,相当于将编码器的输出电平增大 1 倍再加上该段落的 量化电平,为了与抽样值进行比较,认为译码输出为 608+32/2=624。 【例 7-8】 设简单增量调制器输入的正弦信号频率为 3.4 kHz、幅度为 1 V,若抽样频 率 fs=32 kHz,求量阶σ。 解 正弦信号最大斜率为 Aω=1×2π×3.4×103 为使ΔM 不过载,必须满足 Aω≤σfs 由此得 σ≥ 3 3 32 10 2 3.4 10 = s f A V=0.67V 【例 7-9】 对 10 路带宽均为 300~3400 Hz 的模拟信号进行 PCM 时分复用传输。抽样 速率为 8000 Hz,抽样后进行 8 级量化,并编为自然二进制码,码元波形是宽度为τ的矩形 脉冲,且占空比为 1。试求传输此时分复用 PCM 信号所需的最小带宽(设码流中无帧同步码