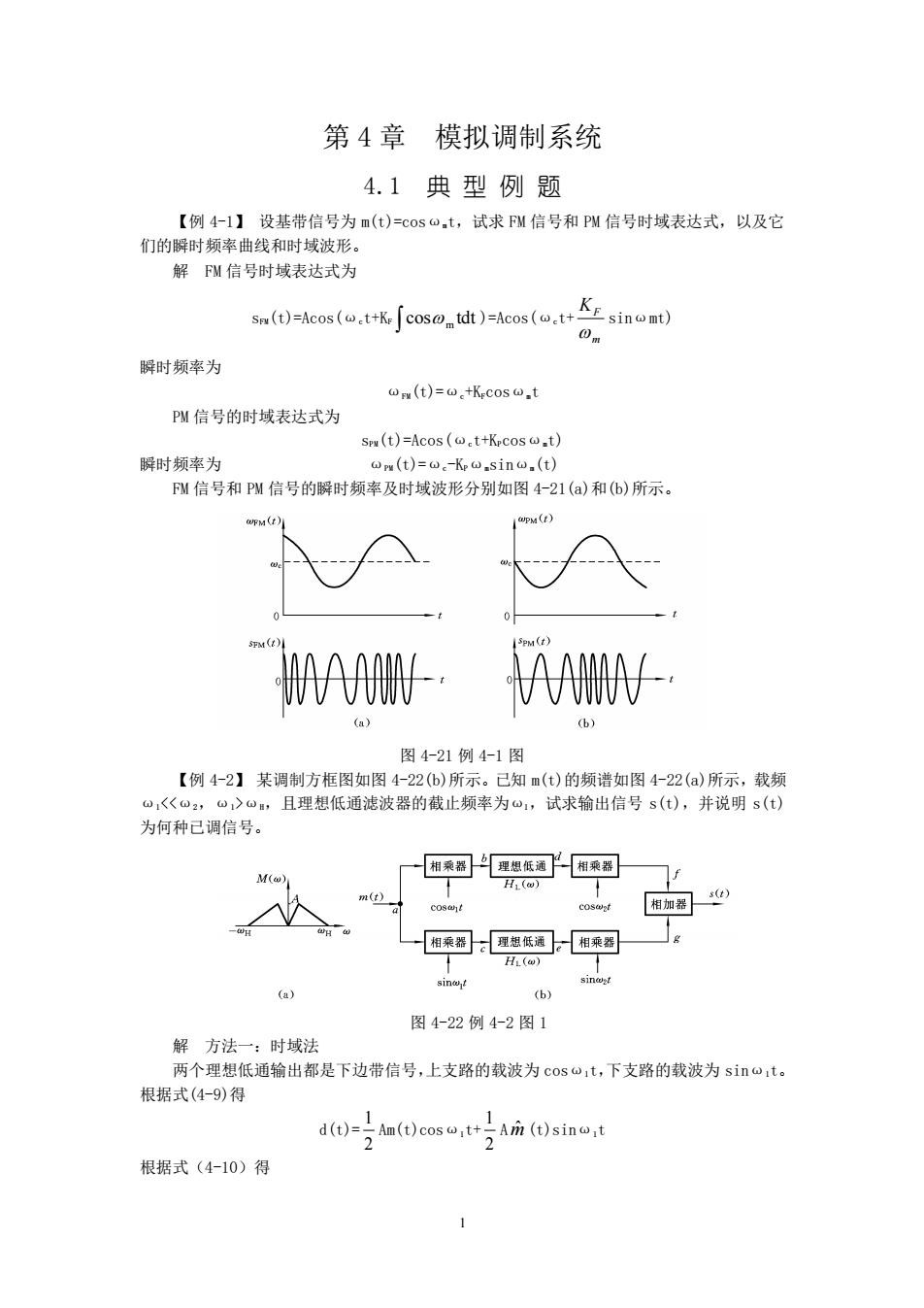
第4章模拟调制系统 4.1典型例题 【例41】设基带信号为m()=cos@,t,试求W信号和PW信号时域表达式,以及它 们的瞬时频率曲线和时域波形。 解W信号时域表达式为 m(t)-cos()=Acos() 瞬时频率为 n(t)=w.+K:cosw.t PW信号的时域表达式为 sw(t)=Acos(w.t+Krcosw.t) 瞬时频率为 wm(t)=w.-Krwsinw.(t) FM信号和PW信号的瞬时频率及时域波形分别如图4-21(a)和(6)所示。 aM】 PM C MAAAW- (a) 图4-21例4-1图 【例4-2】某调制方框图如图4-22(b)所示。已知m(t)的频谱如图4-22()所示,载频 a1〈《o2,。>u,且理想低通滤波器的截止频率为o,试求输出信号s(t),并说明s(t) 为何种已调信号。 M(o 一一超桑司理思润-西来司V 一相来司:里电低国-附来剂: a) (b) 图4-22例4-2图1 解方法一:时域法 两个理想低通输出都是下边带信号,上支路的载波为cos,t,下支路的载波为sin~t 根据式(4-9)得 根据式(4-10)得
1 第 4 章 模拟调制系统 4.1 典 型 例 题 【例 4-1】 设基带信号为 m(t)=cosωmt,试求 FM 信号和 PM 信号时域表达式,以及它 们的瞬时频率曲线和时域波形。 解 FM 信号时域表达式为 sFM(t)=Acos(ωct+KF cos tdt m )=Acos(ωct+ m KF sinωmt) 瞬时频率为 ωFM(t)=ωc+KFcosωmt PM 信号的时域表达式为 sPM(t)=Acos(ωct+KPcosωmt) 瞬时频率为 ωPM(t)=ωc-KPωmsinωm(t) FM 信号和 PM 信号的瞬时频率及时域波形分别如图 4-21(a)和(b)所示。 图 4-21 例 4-1 图 【例 4-2】 某调制方框图如图 4-22(b)所示。已知 m(t)的频谱如图 4-22(a)所示,载频 ω1<<ω2,ω1>ωH,且理想低通滤波器的截止频率为ω1,试求输出信号 s(t),并说明 s(t) 为何种已调信号。 图 4-22 例 4-2 图 1 解 方法一:时域法 两个理想低通输出都是下边带信号,上支路的载波为 cosω1t,下支路的载波为 sinω1t。 根据式(4-9)得 d(t)= 2 1 Am(t)cosω1t+ 2 1 A m ˆ (t)sinω1t 根据式(4-10)得

e(t)-m(t)sin (t)cos,t 由此得 s(t)=f(t)+g(t) ((cossi((sinsin -Am(t)cos(-)t-(t)sin()t 可知,s(t)是一个载频为ω2-01的上边带信号。 方法二:频域法 上支路各点信号的频谱表达式为 soj-号a*-o1(oy S(w)-4 [S(w+w)+S(w-w)] 下支路各点信号的频谱表达式为 so)号(oa(e-o】 s()() -{[u(u+u)-(a-u)]L(o)}*[8(o-o,-6(u+o] S(u)=S:(u)+S.(u) 各点信号频谱图如图4-23所示。由图可知,s()是一个载频为:ω的上边带信号 s()-Aa(t)cos(w:-)t-Ai (t)sin(w:-)t
2 e(t)= 2 1 Am(t)sinω1t- 2 1 A m ˆ (t)cosω1t 由此得 s(t)=f(t)+g(t) = 2 1 Am(t)(cosω1t+sinω1t)cosω2t+ 2 1 A m ˆ (t)(sinω1t-cosω1t)sinω 2t = 2 1 Am(t)cos(ω2-ω1)t-= 2 1 A m ˆ (t)sin(ω2-ω1)t 可知,s(t)是一个载频为ω2-ω1 的上边带信号。 方法二:频域法 上支路各点信号的频谱表达式为 Sb(ω)= 2 A [M(ω+ω1)+M(ω-ω1)] Sd(ω)= 2 A [M(ω+ω1)+M(ω-ω1)]HL(ω) Sf(ω)= 4 A [Sd(ω+ω2)+Sd(ω-ω2)] 下支路各点信号的频谱表达式为 Sc(ω)= 2 jA [M(ω+ω1)-M(ω-ω1)] Se(ω)= 2 jA [M(ω+ω1)-M(ω-ω1)]HL(ω) Sg(ω)= 2 1 ·Se(ω)* j [δ(ω+ω2)-δ(ω-ω2)] = 4 A [M(ω+ω1)-M(ω-ω1)]HL(ω) *[δ(ω-ω2)-δ(ω+ω2)] S(ω)=Sf(ω)+Sg(ω) 各点信号频谱图如图 4-23 所示。由图可知,s(t)是一个载频为ω2-ω1 的上边带信号, 即 s(t)= 2 1 Am(t)cos(ω2-ω1)t- 2 1 A m ˆ (t)sin(ω2-ω1)t
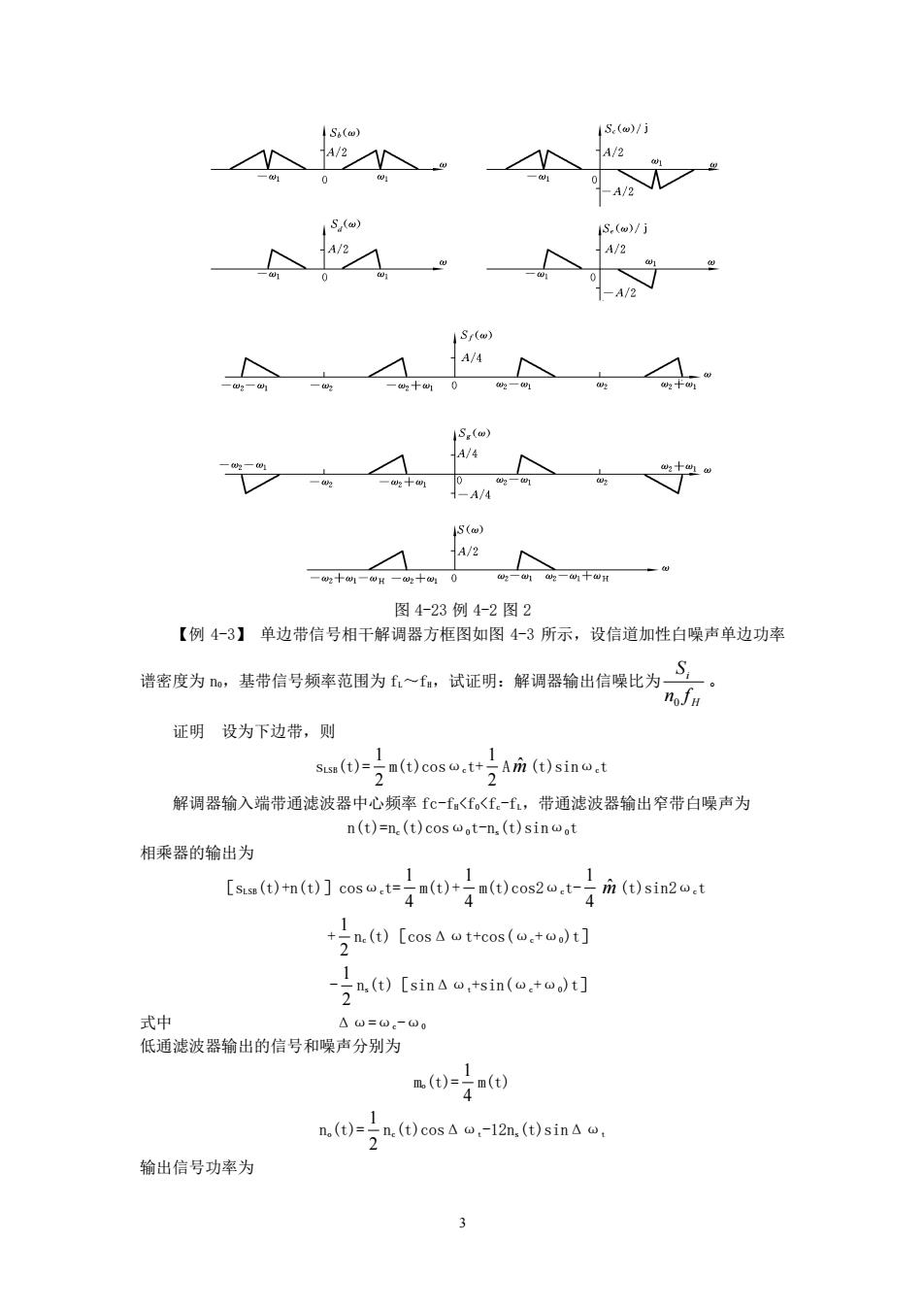
S,w】 A/4 图4-23例4-2图2 【例4-3】单边带信号相干解调器方框图如图4-3所示,设信道加性白噪声单边功率 谱密度为,基带信号频率范围为~,试证明:解调器输出信噪比为 证明设为下边带,则 sa(t)()cos.t ()sino.t 解调器输入端带通滤波器中心频率fc-f<f<f-f,带通滤波器输出窄带白噪声为 n(t)=n(t)cost-n.(t)sinwot 相乘器的输出为 [s(t)+n(t)]co.(t)cos2.()sin2.t 式中 △0=0-00 低通滤波器输出的信号和噪声分别为 n0-分0eas4ol2 .()in 输出信号功率为
3 图 4-23 例 4-2 图 2 【例 4-3】 单边带信号相干解调器方框图如图 4-3 所示,设信道加性白噪声单边功率 谱密度为 n0,基带信号频率范围为 fL~fH,试证明:解调器输出信噪比为 H i n f S 0 。 证明 设为下边带,则 sLSB(t)= 2 1 m(t)cosωct+ 2 1 A m ˆ (t)sinωct 解调器输入端带通滤波器中心频率 fc-fH<f0<fc-fL,带通滤波器输出窄带白噪声为 n(t)=nc(t)cosω0t-ns(t)sinω0t 相乘器的输出为 [sLSB(t)+n(t)]cosωct= 4 1 m(t)+ 4 1 m(t)cos2ωct- 4 1 m ˆ (t)sin2ωct + 2 1 nc(t)[cosΔωt+cos(ωc+ω0)t] - 2 1 ns(t)[sinΔωt+sin(ωc+ω0)t] 式中 Δω=ωc-ω0 低通滤波器输出的信号和噪声分别为 mo(t)= 4 1 m(t) no(t)= 2 1 nc(t)cosΔωt-12ns(t)sinΔωt 输出信号功率为

sGm可 输出噪声功率 ow(co(cos()()sin2A 因n.(t)与n(t)在同一时刻不相关,cos2△u,与sin2△u:及n.(t)、n,(t)不相关, n2()=m,(),所以 g0gn0-0-6 解调器输入信号功率 sSa0-gm0+gm0eoa2ut"g[aw]2 因为 M()=[-jsgn()].M() 所以 [M(o)]=[M(o)]: 可见m(t)的功率与m(t)的功率是相等的。因为t()及[m()]与cos2.t不相关,m(t)、 m(t)与si2“t不相关,所以解调器输入信号功率为 Smm()cos2m ()2cos2. r阿a0si2or可 解调器输出信噪比 N。 命题证毕。 【例4-4】设某信道具有均匀的双边噪声功率谱密度P.()=0.5×103W/z,在该信道 中传输抑制载波的双边带信号,并将调制信号m(t)的频带限制在5kz,而载波频率为100 kz,己调信号的功率为10kW,若接收机的输入信号在加至解调器之前,先经过带宽为10k 的一理想带通滤波器滤波,试问: ()该理想带通滤波器中心频率为多大 (②)解调器输入端的信噪功率比为多少? (③)解调器输出端的信噪功率比为多少? (④)求出解调器输出端的噪声功率谱密度,并用图形表示出米。 解(1)滤波器中心频率为100kz。 (③)输出信噪功率比为 S./N,=G(S/N)=2X10 (④)解调器输出噪声n(t)为
4 So= 16 1 ( ) 2 m t 输出噪声功率 No= n o (t) 2 = 8 1 n c (t) 2 (1+cos2Δωt)+ 8 1 n c (t) 2 (1-cos2Δωt)- 4 1 nc(t)ns(t)sin2Δωt 因 nc(t)与 ns(t)在同一时刻不相关,cos2Δωt 与 sin2Δωt 及 nc(t)、ns(t)不相关, n 2 c(t)=n2 s(t),所以 No= 8 1 n c (t) 2 +1 8 1 n c (t) 2 = 4 1 n 2 c(t)= 4 1 n0fH 解调器输入信号功率 Si ( ) 2 S LSB t = 8 1 ( ) 2 m t + 8 1 ( ) 2 m t cos2ωct+ 8 1 [ m ˆ (t)]2 - 8 1 [ m ˆ (t)]2cos2ωct- 4 1 m(t) m ˆ (t)sin2ωct 因为 M ˆ (ω)=[-jsgn(ω)]·M(ω) 所以 [ M ˆ (ω)] 2 =[M(ω)] 2 可见 m(t)的功率与 m ˆ (t)的功率是相等的。因为 m 2 (t)及[ m ˆ (t)]2 与 cos2ωct 不相关,m(t)、 m ˆ (t)与 sin2ωct 不相关,所以解调器输入信号功率为 Si= ( ) 4 1 2 m t + ( ) 8 1 2 m t cos2ωct- 8 1 [ m ˆ (t)]2cos2ωct - ( ) 4 1 2 m t m ˆ (t)·sin2ωct= ( ) 4 1 2 m t 解调器输出信噪比 H H o o n f m t n f m t N S 0 2 0 2 ( ) 4 1 4 1 ( ) 16 1 = = = H i n f S 0 命题证毕。 【例 4-4】 设某信道具有均匀的双边噪声功率谱密度 Pn(f)=0.5×10-3 W/Hz,在该信道 中传输抑制载波的双边带信号,并将调制信号 m(t)的频带限制在 5 kHz,而载波频率为 100 kHz,已调信号的功率为 10 kW。若接收机的输入信号在加至解调器之前,先经过带宽为 10 kHz 的一理想带通滤波器滤波,试问: (1) 该理想带通滤波器中心频率为多大? (2) 解调器输入端的信噪功率比为多少? (3) 解调器输出端的信噪功率比为多少? (4) 求出解调器输出端的噪声功率谱密度,并用图形表示出来。 解 (1) 滤波器中心频率为 100 kHz。 (2) Ni=2Pn(f)×2fH=(4×0.5×10-3×5×103 ) W=10 W 输入信噪功率比为 Si/Ni=10×103 /10=103 (3) 输出信噪功率比为 So/No=G(Si/Ni)=2×103 (4) 解调器输出噪声 no(t)为

(n(t)cos,t-n(t)sinw.tcos.tLPE(t) 所以n(t)的功率谱密度为 m0-月0-D25x103w1trs5x10 0,.其它 P.(f 5×10- P()的图形如图4-24所示。 【例4-5】设本地载波与发送载波的频率误差和相位误差分别为△“和 -505f/H △Φ,试分析对DSB信号相干解调结果的影响。 图4-24例4-4图 解本地载波与DSB信号相乘后为 sa(t)·c(t)=m(t)cosw.tcos(o:t+△ot+△中) ()cos(co) 经LPF后得到 a(0=))cos(A0+A) 可见,若△“=0,则解调输出功率下降,即相位误差使解调输出功率下降。若△≠0,则 解调输出发生失真。 【例4-6】试证明:当AM信号采用同步检波法进行解调时无门限效应。 证明相乘器输入信号和噪声分别为 sw(t)=[A+m(t)]coso.t n(t)=n.(t)cosw.t 相乘器输出为 有4+m]cos。1-n.(0coso.t-n,0sino.1coso.l =A+m】+[A+m(cos2o. +7n.0+2.0cos201-7n,0sn2a1 低通滤波器输出信号和噪声分别为 L()=5n() n(t)-zn(t) 输出信噪比为 是 输入信号功率为 S-5iav(=++]
5 (nc(t)cosωct-ns(t)sinωctcosωct 2 1 LPF nc(t) 所以 no(t)的功率谱密度为 Pno(f)= 4 1 nc P (f)= 其它 0, 0.25 10 W/Hz, | f | 5 10 -3 3 nc P (f)的图形如图 4-24 所示。 【例 4-5】设本地载波与发送载波的频率误差和相位误差分别为Δω和 Δφ,试分析对 DSB 信号相干解调结果的影响。 图 4-24 例 4-4 图 解 本地载波与 DSB 信号相乘后为 sDSB(t)·c(t)=m(t)cosωct·cos(ωct+Δωt+Δφ) = 2 1 m(t)cos(Δωt+Δφ)+ 2 1 m(t)cos(2ωct+Δωct+Δφ) 经 LPF 后得到 mo(t)= 2 1 m(t)cos(Δωt+Δφ) 可见,若Δω=0,则解调输出功率下降,即相位误差使解调输出功率下降。若Δω≠0,则 解调输出发生失真。 【例 4-6】 试证明:当 AM 信号采用同步检波法进行解调时无门限效应。 证明 相乘器输入信号和噪声分别为 sAM(t)=[A+m(t)]cosωct n(t)=nc(t)cosωct 相乘器输出为 A m t t n t t n t t t c c c s c c [ + ( )]cos − ( )cos − ( )sin cos n t n t t n t t A m t A m t t c c c s c c ( )sin 2 2 1 ( ) cos 2 2 1 ( ) 2 1 [ ( )]cos 2 2 1 [ ( )] 2 1 + + − = + + + 低通滤波器输出信号和噪声分别为 mo(t)= 2 1 m(t) no(t)= 2 1 nc(t) 输出信噪比为 ( ) ( ) 2 n t m t N S o c o = 输入信号功率为 Si= [ ( )] 2 1 [ ( )] 2 1 ( ) 2 2 2 2 S t A m t A m t AAM = + = +