
概華论与款醒统外 离散型随机变量的分布律 ()定义 设离散型随机变量X所有可能取的值为xx (k=1,2,),X取各个可能值的概率,即事件 {X=x}的概率,为 P{X=Xk}=pk,k=1,2,. 称此为离散型随机变量X的分布律
. { } , 1,2, . { } , ( 1,2, ), , 称此为离散型随机变量 的分布律 的概率 为 取各个可能值的概率 即事件 设离散型随机变量 所有可能取的值为 X P X x p k X x k X X x k k k k = = = = = 离散型随机变量的分布律 (1)定义
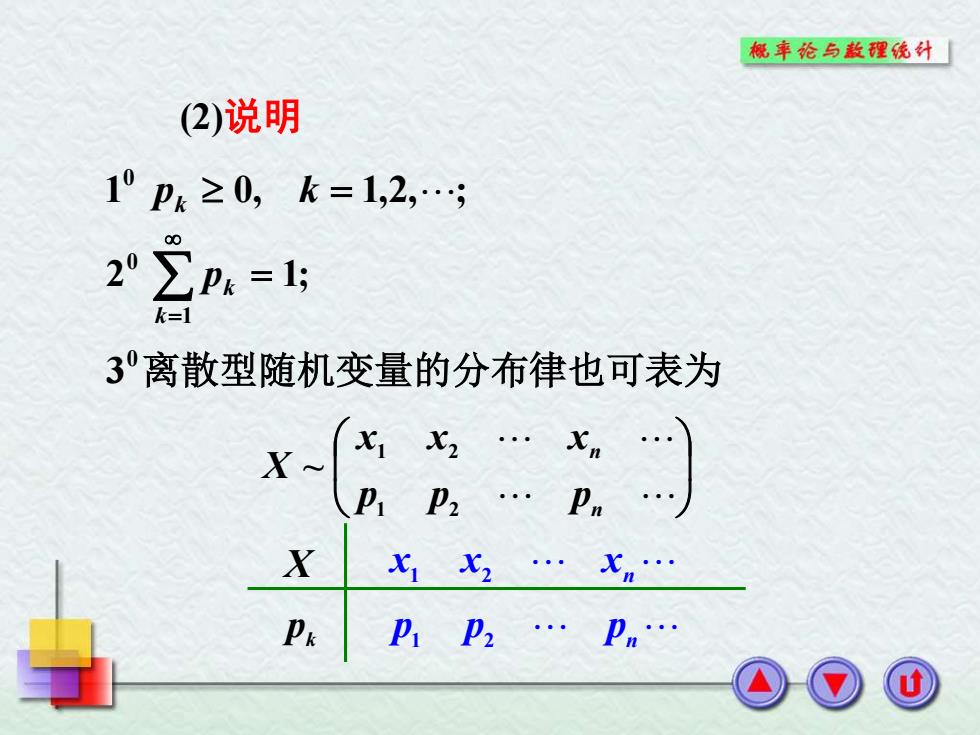
概车纶与款理统外 (2)说明 1°pk≥0,k=1,2, 00 2”∑p&=l5 k=1 3离散型随机变量的分布律也可表为 X x12. Xn P P2 X 2.xn. Pk PP.Pm
n n p p p x x x X 1 2 1 2 ~ X pk x1 x2 xn p1 p2 pn 1 0, 1,2, ; 0 pk k = 2 1; 1 0 = k= pk (2)说明 3 0离散型随机变量的分布律也可表为

概華论与款醒统外 两点分布 设随机变量X只可能取0与1两个值,它的分 布律为 X 0 1 P& 1-p 则称X服从(0-1)分布或两点分布
设随机变量 X 只可能取0与1两个值 , 它的分 布律为 X pk 0 1− p 1 p 则称 X 服从(0-1)分布或两点分布. 两点分布

概车纶与款理统外 二项分布 X的分布律为 P{X=}=Cp(I-p)”- (k=0,1,2,.,n,0<p<1) 称这样的分布为二项分布.记为X~(n,p). 二项分布 n=1. 两点分布
称这样的分布为二项分布.记为 X ~ b(n, p). X的分布律为 (k = 0,1,2, ,n, 0 p 1) 二项分布 n = 1 两点分布 二项分布 { } (1 ) k k n k P X k C p p n − = = −

概華论与款醒硫外 泊松分布 设随机变量所有可能取的值为0,1,2,.,而取 各个值的概率为 P==e e! ,k=0,1,2,.) 其中入>0是常数.则称X服从参数为入的泊松分 布,记为X~(2)
, ~ π( ). 0 . , 0,1,2, , ! e { } 0,1,2, , X X k k P X k k 布 记为 其中 是常数 则称 服从参数为 的泊松分 各个值的概率为 设随机变量所有可能取的值为 而取 = = = − 泊松分布