《高等数学》课程教学资源（PPT课件）第九章 多元函数的微分法及其应用_第三节 全微分_全微分

第三讲 ，全微分

第三讲 全微分

全微分 一、 全微分的概念 二、全微分的存在条件 三、全微分的运算 四、全微分的应用

全微分 一、全微分的概念 二、全微分的存在条件 三、全微分的运算 四、全微分的应用

全微分 一、金微分的概念 二、全微分的存在条件 三、全微分的运算 四、全微分的应用

全微分 一、全微分的概念 二、全微分的存在条件 三、全微分的运算 四、全微分的应用

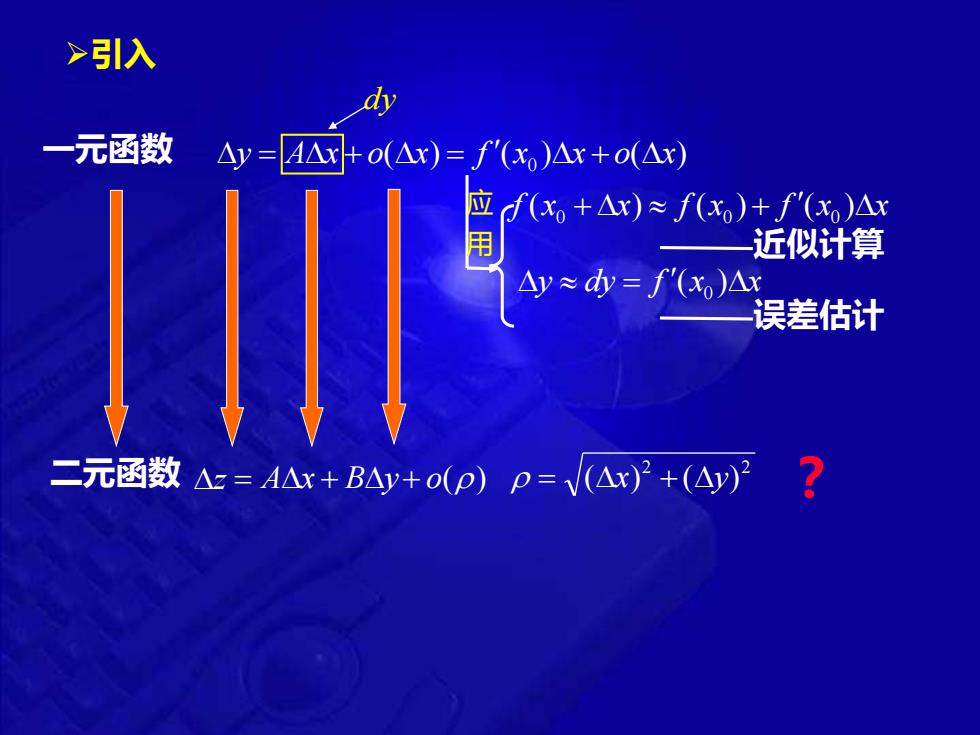
>引入 一元函数 △y=A△☒+o(△x)=f'(x)△x+o(△x) 4 +)≈ftx 一近似计算 Ay≈=f'(x)△ 误差估计 二元函数△z=A△x+B△y+o(p)p=VAx)2+(A)?

➢引入 一元函数 y = A x + o ( x ) ( ) ( ) 0 = f  x x + o x 应用 f ( x + x )  f ( x ) + f ( x ) x 0 0 0 近似计算 y  dy = f ( x ) x 0 dy 误差估计 二元函数 z = A x + B y + o ( ) 2 2  = ( x ) + ( y ) ？

>定义 设函数：=f(化，y)在点cy)的某邻域内有定义，如果函数 在点化，y)处的全增量△：=f(x+△x,y+△y)-f(x,y)可表示为 △z=A△x+B△y+0(P),其中A,B不依赖于△x,△y而仅与x,Jy 有关P=(△x)+(△y),那么称函数f化，y)在点化，y)可微分， 而A△x+B△称为函数zf(xy)在点化y)的全微分，记作dk 即dz=A△x+B△y ●注 △x与△的线性函数dz=A△x+BAy dz的特性 与△相差一个比p高阶的无穷小量 与△x和△y无关 A、B的特性 仅与和有关

➢定义 ⚫注 dz的特性 Δx与Δy的线性函数 与Δz相差一个比ρ高阶的无穷小量 A、B的特性 与Δx和Δy无关 仅与x和y有关 设函数z = f (x, y)在点(x,y)的某邻域内有定义，如果函数 可表示为  z = Ax + B  y + o( ) , 其中A,B不依赖于x, y 而仅与x, y Ax + By 称为函数z=f (x,y)在点(x,y)的全微分，记作 在点(x, y)处的全增量 有关， 那么称函数f (x, y)在点(x, y)可微分， 而 dz 即 dz = Ax + By. dz = Ax + By