
第四讲 多元拯数微分学概念习题课
第四讲 多元函数微分学概念习题课

多元函数微分学概念习题课 一、内容小结 二、题型练习
多元函数微分学概念习题课 一、内容小结 二、题型练习

多元函数微分学概念习题课 一、内容小结 二、题型练习
多元函数微分学概念习题课 一、内容小结 二、题型练习
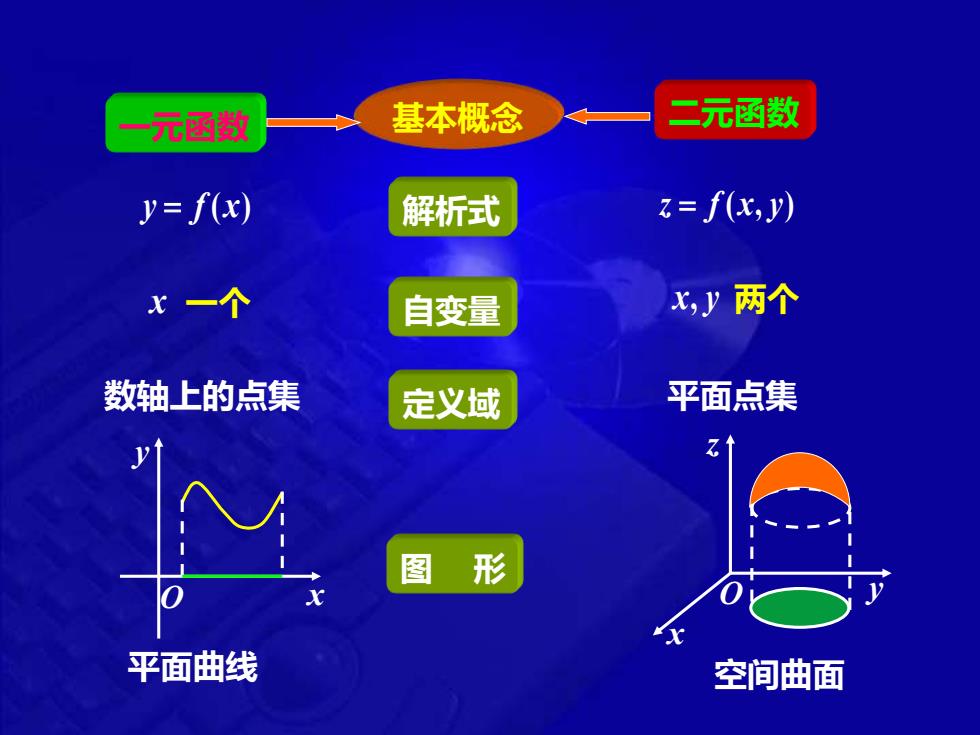
元函数 基本概念 二元函数 y=f(x) 解析式 z=f(x,y) x一个 自变量 x,y两个 数轴上的点集 定义域 平面点集 图 形 平面曲线 空间曲面
一元函数 基本概念 二元函数 y = f (x) 解析式 z = f (x, y) x 一个 自变量 x, y 两个 数轴上的点集 定义域 平面点集 图 形 O x y x O z y 平面曲线 空间曲面

元函数 基本概念 二元函数 limf(x)=A之 lim f(x,y)=A x→x0 极 限 (x,xn】 f(x)=f(x)=A 任何路径的极限都等于A lim f(x)=f(x) 连 续 imf(化,y)=f(xo,yo) x->xo (xJx%)】 f(xo,Yo)= f"(x)=lim f(x,+△x)-f(x, △x-0 △Y (偏)导数 lim f(x+△x,yo)-f(x,Jy) △x→0 △x ffyfrFo f"(x) 高阶导数 混合偏导数连续时相等 dy=f(x)dx (全)微分 dz= 0 d此+ dy Ox a
一元函数 基本概念 二元函数 极 限 连 续 (偏)导数 (全)微分 高阶导数 f x A x x = → lim ( ) 0 f x y A x y x y = → lim ( , ) ( , ) ( , ) 0 0 f x = f x = A + − ( ) ( ) 0 0 任何路径的极限都等于A lim ( ) ( ) 0 0 f x f x x x = → lim ( , ) ( , ) 0 0 ( , ) ( , ) 0 0 f x y f x y x y x y = → x f x x f x f x x + − = → ( ) ( ) ( ) lim 0 0 0 f x (x0 , y0 ) = x f x x y f x y x + − → ( , ) ( , ) lim 0 0 0 0 0 f (x) f xx , f xy , f yx , f yy , 混合偏导数连续时相等 dy = f (x)dx y y z x x z dz d d + =