
第七节 函数的连续性 一、 函数的连续性 二、函数的间断点 三、初等函数的连续性 四、闭区间上连续函数的性质 五、小结 ☑合
第七节 函数的连续性 一、函数的连续性 二、函数的间断点 三、初等函数的连续性 四、闭区间上连续函数的性质 五、小结

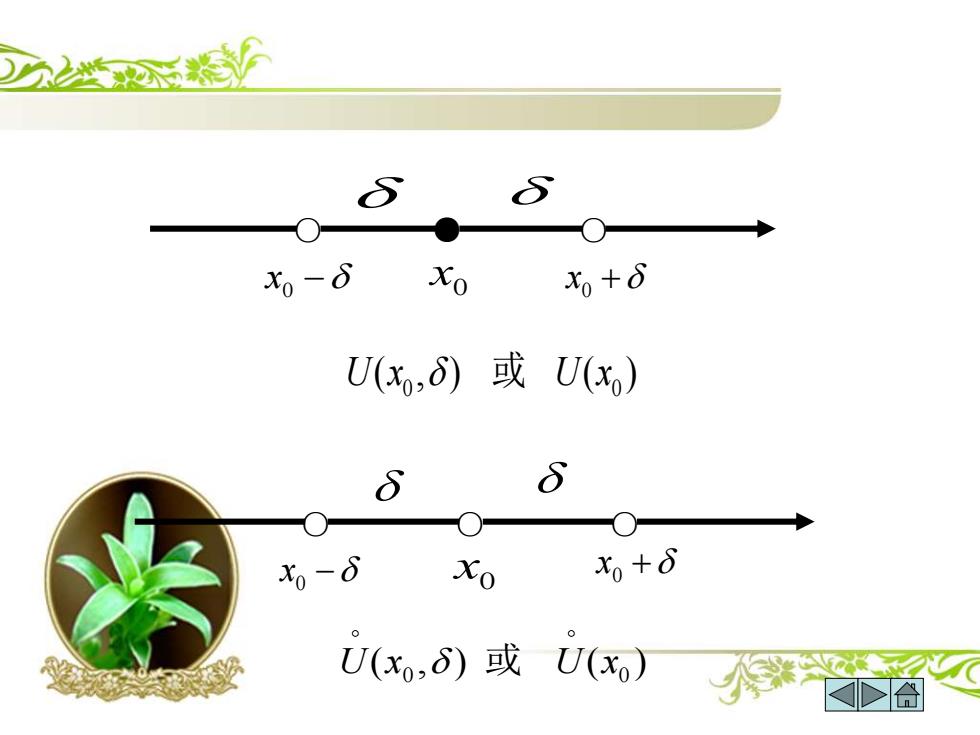
邻域与空心邻域(补从内容) 设x。∈R,6>0,称开区间(x。-6,x。+6)为点x的邻域, 记为U(x,δ), 即U(x,6)=(x。-6,x。+6)={x‖x-xKδ}, x为邻域的中心,δ为邻域的半径 将的s邻域中心x去掉后得x,的6空心邻域,记为U°(x,δ) =(x-δ,x)U(xo,x+δ)={x|0x-xkδ} 或及空心邻域分别简记为U(x)与U°(x)
邻域与空心邻域(补从内容) ( , ), , 0, ( , ) 0 0 0 0 0 U x x R x x x 记为 设 称开区间 − + 为点 的 邻域, 0 0 0 0 即U x x x x x x ( , ) ) { || | }, = − + = − ( , x0 为邻域的中心,为邻域的半径 o 0 0 0 0 将x x x U x 的 邻域中心 去掉后得 的 空心邻域,记为 ( , ), o 0 0 0 0 0 0 即U x x x x x x x x ( , ) { | 0 | | } = − + = − ( , )( , ) 0 0 0 ( ) ( ) o 点x U x U x 的邻域及空心邻域分别简记为 与
S S x,-6 Xo x0+6 U(x,6)或U(x) δ 8 七,-6 Xo x0+6 U(x,)或U(x) ✉囧
○ ● ○ x0 − x0 + 0 x x0 − x0 + 0 x ○ ○ ○ ( , ) ( ) 0 0 U x U x 或 ( , ) ( ) 0 0 U x 或 U x

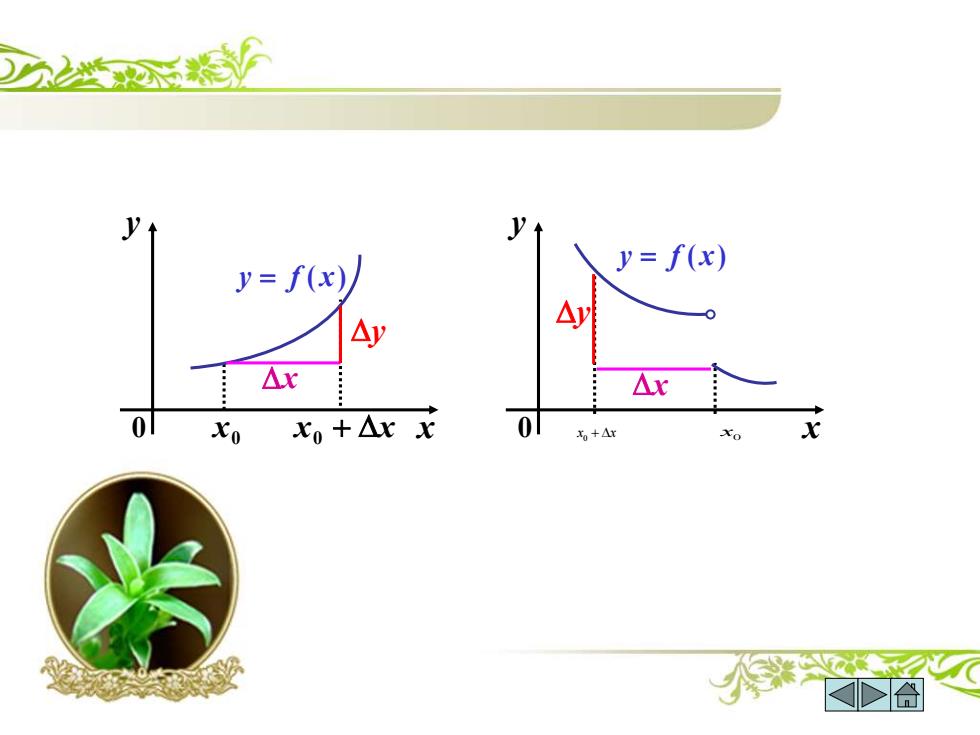
函数的连续性 1.函数的增量 设函数f(x)在U(x)内有定义,廿x∈U(x), △x=x-x,称为自变量在点x,的增量 x:x0→x0+△x △y=f(x)-f(x),称为函数f(x)相应于△x的增量 f(x):f(x)→f(x+△) 作米吃 ✉合
一、函数的连续性 1. 函数的增量 0 0 0 0 ( ) ( ) , ( ), , . f x U x x U x x x x x = − 设函数 在 内有定义 称为自变量在点 的增量 ( ) ( ), ( ) . y = f x − f x0 称为函数 f x 相应于x的增量 x x → x + x 0 0 : ( ): ( ) ( ) 0 0 f x f x → f x + x
y=f(x) y=f(x) y Ay △x △x 0 Xo xo+△xx 0 Xo
x y 0 x0 x0 + x y = f ( x) x y x y 0 x + x 0 x0 x y y = f ( x)