§1 单纯形表的灵敏度分析 迭代 X1 X2 S1 S2 3 比值 基变量 CB 次数 S0 100 0 0 0 blai X1 601 1 0 1 0 -1 50 S2 0 0 0 -2 1 1 50 X2 100 0 1 0 1 250 501 100 01 0 -c'1100 27500 0=G冯 0 0 01 0 c'1e00 1、用c'1代替原来的c1=50 3、从o≤0,得c1≤100 0Sc'≤100,若c超出取值范围,必存在检验数>0,可通过迭代来得到新 的最优解
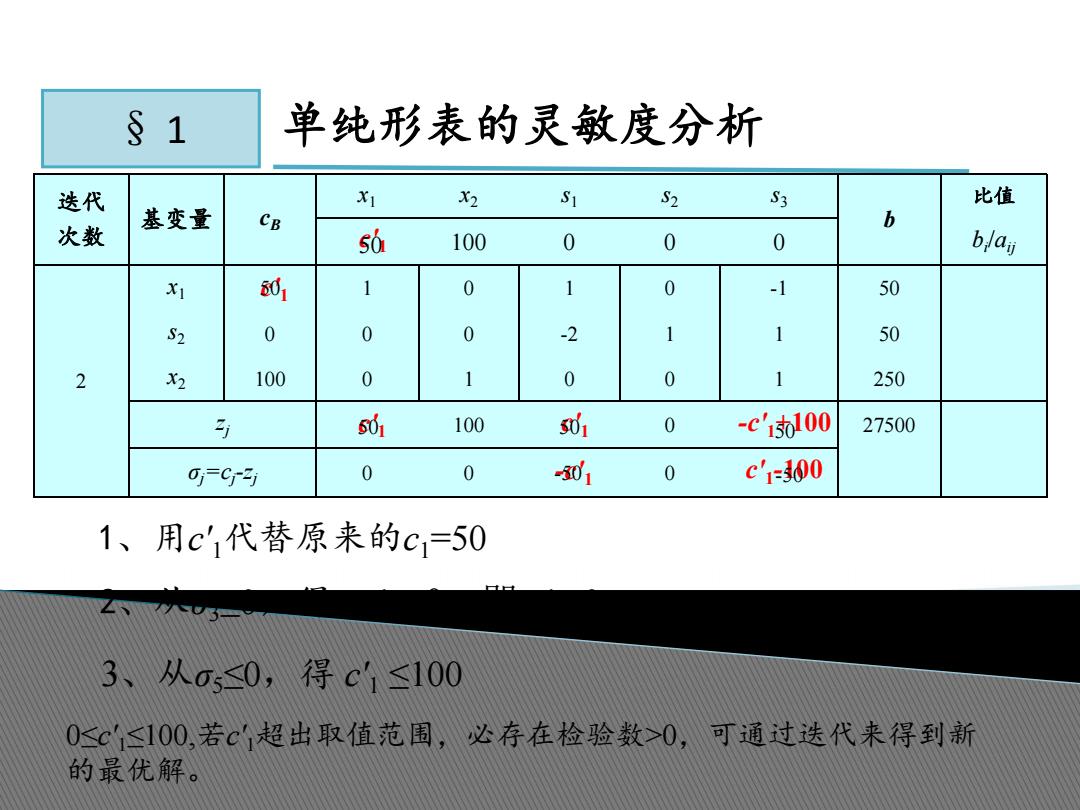
§ 1 单纯形表的灵敏度分析 2、从σ3≤0,得− c' 1 ≤0,即 c' 1≥0 1、用c' 1代替原来的c1=50 迭代 次数 基变量 cB x1 x2 s1 s2 s3 b 比值 100 0 0 0 bi/aij 2 x1 1 0 1 0 -1 50 s2 0 0 0 -2 1 1 50 x2 100 0 1 0 0 1 250 zj 100 0 27500 σj=cj-zj 0 0 -c' 1 0 c' 1 c' 1 c' 1 c' 1 -c' 1+100 c' 1-100 50 50 50 50 -50 50 -50 3、从σ5≤0,得 c' 1 ≤100 0≤c' 1≤100,若c' 1超出取值范围,必存在检验数>0,可通过迭代来得到新 的最优解

§1 单纯形表的灵敏度分析 Ck x为非基变量)Ck十△Ck 当△c2Ok,即△c2Zk时,Xk变为入基变量。由△C3≤50, 最优解不变。 C3 :0→50 剩余单位台时数设备:从不获利到获利50元时 若有人出50元买1个设备台时,厂家则不必为生产|、 从而设各业鱼柔痰里欧的婆备余时白样可知后杜A 的对偶价格为40心,你
§ 1 单纯形表的灵敏度分析 当Δck≥−σk,即Δck≥zk时,xk变为入基变量。由Δ c3 ≤50 , 最优解不变。 k k k x k c c c 为非基变量 剩余单位台时数设备:从不获利到获利50元时 从而设备台时数的对偶价格为z3=50元。同样可知原料A 的对偶价格为z4=0元,原料B的对偶价格为 z5=50 元。 c3 : 0 →50 若有人出50元买1个设备台时,厂家则不必为生产Ⅰ、 Ⅱ产品而使用完所有的设备台时

§1 单纯形表的灵敏度分析 由最终单纯形表对于不同约束类型的对偶价格的取值如下表: 约束类型 对偶价格的取值 ≤ 等于该约束条件对应的松弛变量的z,值 ≥ 等于该约束条件对应的剩余变量的相反数 等于该约束条件对应的人工变量的z,值 从对偶价格的定义可知,当对偶价格为正,将改进目标函数值, 当对偶价格为负,将“恶化”目标函数值
§ 1 单纯形表的灵敏度分析 由最终单纯形表对于不同约束类型的对偶价格的取值如下表: 从对偶价格的定义可知,当对偶价格为正,将改进目标函数值, 当对偶价格为负,将“恶化”目标函数值。 约束类型 对偶价格的取值 ≤ 等于该约束条件对应的松弛变量的zj值 ≥ 等于该约束条件对应的剩余变量zj的相反数-zj = 等于该约束条件对应的人工变量的zj值

§1 单纯形表的灵敏度分析 在求目标函数最大值的线性规划中,对偶价格等于影子价格; 求目标函数最小值时,影子价格为对偶价格的相反数。 影子价格的取值 约束类型 求目标函数最大值 求目标函数最小值 等于该约束条件对应的松弛变 等于该约束条件对应的松弛变 量的z,值 量2,的相反数- 等于该约束条件对应的剩余变 等于该约束条件对应的剩余变 量z的相反数- 量的z,值 等于该约束条件对应的人工变 等于该约束条件对应的人工变 量的z值 量z的相反数
§ 1 单纯形表的灵敏度分析 在求目标函数最大值的线性规划中,对偶价格等于影子价格; 求目标函数最小值时,影子价格为对偶价格的相反数。 约束类型 影子价格的取值 求目标函数最大值 求目标函数最小值 ≤ 等于该约束条件对应的松弛变 量的zj值 等于该约束条件对应的松弛变 量zj的相反数-zj ≥ 等于该约束条件对应的剩余变 量zj的相反数-zj 等于该约束条件对应的剩余变 量的zj值 = 等于该约束条件对应的人工变 量的zj值 等于该约束条件对应的人工变 量zj的相反数-zj

§1 单纯形表的灵敏度分析 二、约束方程中常数项的灵敏度分析b→bk+△b: >由于进行行初等变换,最终单纯形表系数矩阵不变 >基变量系数cB不变 =j=CB'P) >2都不变 >σ都不变,基变量都不变 使其新的最优解的基变量(最优基)都不受, 价格不变的
§ 1 单纯形表的灵敏度分析 求使所得新的解仍可行(≥0)的bj的变化范围,即 使其新的最优解的基变量(最优基)都不变,且其对偶 价格不变的。 二、约束方程中常数项的灵敏度分析 k k k b b b Ø由于进行行初等变换,最终单纯形表系数矩阵不变 Ø基变量系数cB不变 Øzj都不变 j B j z c p Øσj都不变,基变量都不变