
管理运筹学 第三章线性规划在工商 管理中的应用
管理运筹学 第三章 线性规划在工商 管理中的应用

第三章 线性规划在工商管理中的应用 在对线性规划的求解及灵敏度分析的基本概念、 基本原理有所了解之后,我们来研究线性规划 在工商管理中的应用,解决工商管理中的实际 问题
第三章 线性规划在工商管理中的应用 在对线性规划的求解及灵敏度分析的基本概念、 基本原理有所了解之后,我们来研究线性规划 在工商管理中的应用,解决工商管理中的实际 问题

本章内容 ㄖ 人力资源分配的问题 生产计划的问题 套裁下料问题 配料问题 投资问题
人力资源分配的问题 生产计划的问题 套裁下料问题 配料问题 本章内容 1 2 3 4 5 投资问题
§1 人力资源分配的问题 例1.某昼夜服务的公交线路每天各时间段内所需司机和 乘务人员数如下: 班次 时间 所需人数 1 6:00-10:00 60 2 10:00-14:00 70 3 14:00-18:00 60 4 18:00-22:00 50 5 22:00-2:00 20 6 2:00-6:00 30 设司机和乘务人员分别在各时间段开始时上班,并连续工作 公小时问该公交线路应怎样安排司机和乘务人员,既能满 备司机和乘务人员的人数最少?
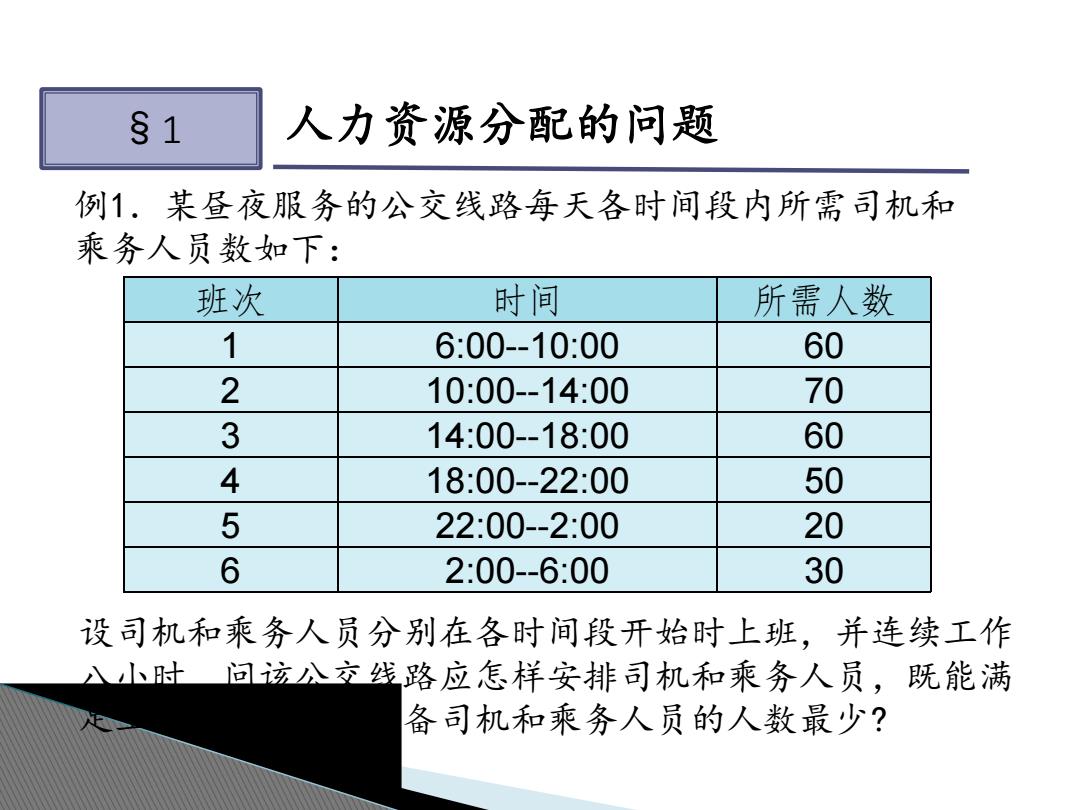
例1.某昼夜服务的公交线路每天各时间段内所需司机和 乘务人员数如下: §1 人力资源分配的问题 设司机和乘务人员分别在各时间段开始时上班,并连续工作 八小时,问该公交线路应怎样安排司机和乘务人员,既能满 足工作需要,又使配备司机和乘务人员的人数最少? 班次 时间 所需人数 1 6:00--10:00 60 2 10:00--14:00 70 3 14:00--18:00 60 4 18:00--22:00 50 5 22:00--2:00 20 6 2:00--6:00 30

§1 人力资源分配的问题 解:设x:表示第ⅰ班次时开始上班的司机和乘务人员人 数,建立如下的数学模型: 目标函数:MinX1+2+名+4+5+6 约束条件: 1+X6 ≥ 60(班次1所需人数) X1+2 ≥70 2+X ≥ 60 X3+4 ≥ 50 X4+X5 ≥20 X5+X6 ≥30 X1,2,3,4,5,6≥0
x1 + x6 ≥ 60(班次1所需人数) §1 人力资源分配的问题 设 xi 表示第i班次时开始上班的司机和乘务人员人 数, 建立如下的数学模型: Min x1 + x2 + x3 + x4 + x5 + x6 x1 + x2 ≥ 70 x2 + x3 ≥ 60 x3 + x4 ≥ 50 x4 + x5 ≥ 20 x5 + x6 ≥ 30 x1,x2,x3,x4,x5,x6 ≥ 0 解: 目标函数: 约束条件: