《管理运筹学》课程教学资源（课件讲义）第五章 单纯形法的灵敏度分析与对偶

管理运筹学 第五章单纯形法的灵敏度分析与对偶

管理运筹学 第五章 单纯形法的灵敏度分析与对偶

本章内容 1 单纯形表的灵敏度分析 2 线性规划的对偶问题 3 对偶规划的基本性质 4 对偶单纯形法种特殊情况

单纯形表的灵敏度分析 线性规划的对偶问题 对偶规划的基本性质 对偶单纯形法种特殊情况 本章内容 1 2 3 4

§1 单纯形表的灵敏度分析 一、 目标函数中变量系数Ck灵敏度分析Ck→Ck+△Ck 1、在最终的单纯形表里，x是非基变量 >由于进行行初等变换，约束方程增广矩阵不变 >基变量系数cB不变 zi=CB'Pj >都不变，包括k Ck→Ck+△Ck Ok=Ck-Zk Ck+△Ck-2k=Ok十△Ck ok+AC:≤0

§ 1 单纯形表的灵敏度分析 一 、目标函数中变量系数 ck 灵敏度分析 1、在最终的单纯形表里，xk是非基变量 Ø由于进行行初等变换，约束方程增广矩阵不变 Ø基变量系数cB不变 Øzj都不变，包括zk j B j z  c  p k k k c  c  c k k c   0 k k   c  k k k k k k k k   c  z c  c  z    c k k k c  c  c 若要原来的最优解不变

§1 单纯形表的灵敏度分析 2.在最终的单纯形表中，x是基变量 >由于进行行初等变换，约束方程增广矩阵不变 >基变量系数c变化 >对所有的z都变化，包括z

§ 1 单纯形表的灵敏度分析 2．在最终的单纯形表中，xk 是基变量 Ø由于进行行初等变换，约束方程增广矩阵不变 Ø基变量系数cB变化 Ø对所有的zj都变化，包括zk j B j z  c  p 假设cB =(cB1 , cB2 ,…, ck ,…,cBm ) (cB1 , cB2 ,…, ck+ck ,…,cBm )

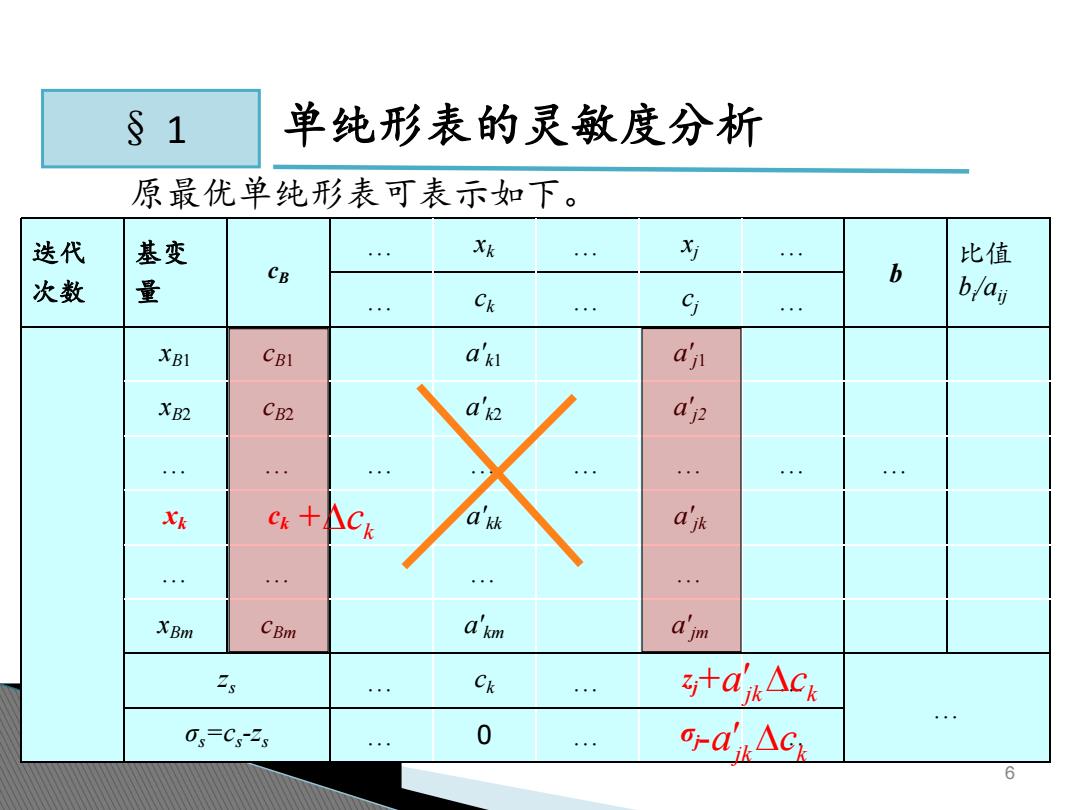
§1 单纯形表的灵敏度分析 原最优单纯形表可表示如下。 迭代 基变 X 5 比值 CB b 次数 量 Ck S b/ai XBI CBI a'k aj XB2 CB2 d'2 a 式k c+Ck a a'jk XBm CBm a'km djm Ck 汁a△ck 0,=C-2g 0 o-dAck 6

6 § 1 原最优单纯形表可表示如下。 单纯形表的灵敏度分析 迭代 次数 基变 量 cB … xk … xj … b 比值 bi … c /aij k … cj … xB1 cB1 a' k1 a' j1 xB2 cB2 a' k2 a' j2 … … … … … … … … xk ck a' kk a' jk … … … … xBm cBm a' km a' jm zs … ck … zj … … σs=cs-zs … 0 … σj … + k c + jk k a  c - jk k a  c