
管理运筹学 第四章单纯形法
管理运筹学 第四章 单纯形法
本章内容 1 单纯形法的基本思路和原理 2 单纯形法的表格形式 求目标函数值最小的线性规划问题的单 3 纯形表解法 几种特殊情况
单纯形法的基本思路和原理 单纯形法的表格形式 求目标函数值最小的线性规划问题的单 纯形表解法 几种特殊情况 本章内容 1 2 3 4
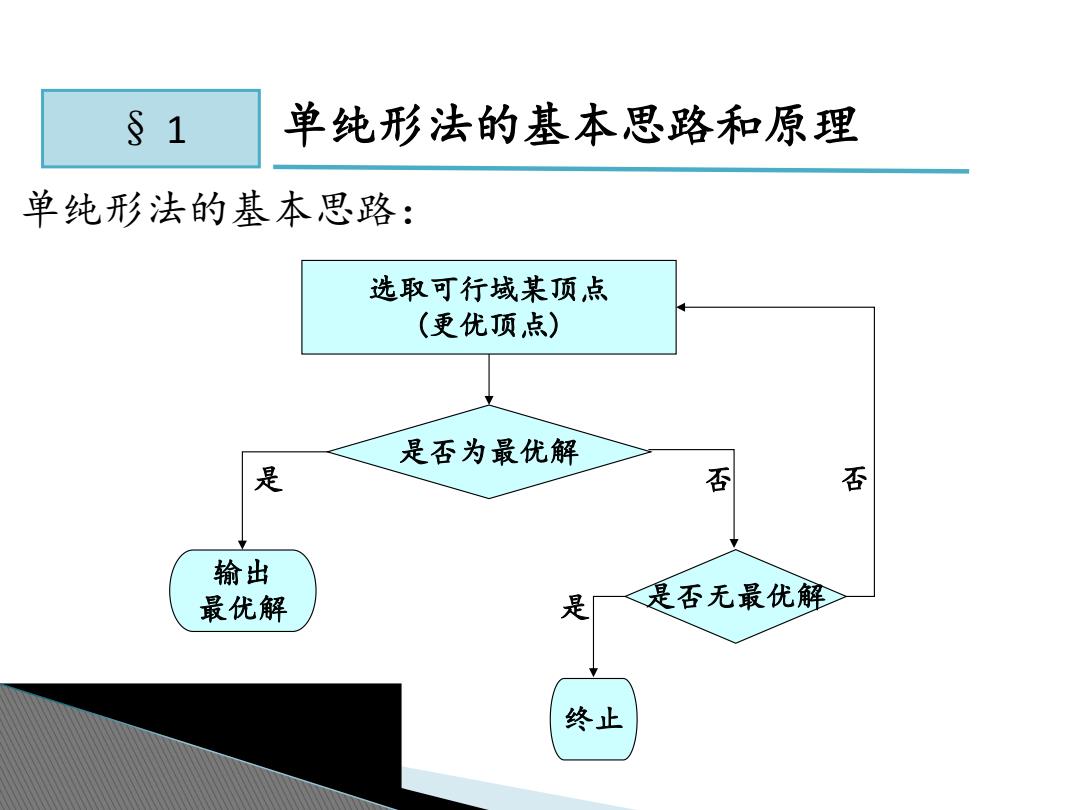
§1 单纯形法的基本思路和原理 单纯形法的基本思路: 选取可行域某顶点 (更优顶点) 是否为最优解 是 否 否 输出 最优解 是 <是否无最优解 终止
§ 1 单纯形法的基本思路和原理 单纯形法的基本思路: 是 否 选取可行域某顶点 (更优顶点) 是否为最优解 输出 最优解 终止 是 是否无最优解 否

§1 单纯形法的基本思路和原理 一、 找出一个初始基本可行解 下面通过第二章例1的求解来介绍单纯形法。 在加上松弛变量之后得到此线性规划的标准形式。 目标函数:max50x1+100x2 约束条件:x1+x2+51=300, 2x1+x2+52=400, x2+S3=250, x,≥0(=1,2),S≥0(=1,2,3)
§ 1 单纯形法的基本思路和原理 一 、找出一个初始基本可行解 下面通过第二章例1的求解来介绍单纯形法。 在加上松弛变量之后得到此线性规划的标准形式。 目标函数:max 50x1+100x2 约束条件:x1+x2+s1=300, 2x1+x2+s2=400, x2+s3=250, xi ≥0(i=1,2),sj≥0(j=1,2,3)

§1 单纯形法的基本思路和原理 该线性规划问题约束方程的系数矩阵为: 711100 A=(p1,P2,P3,P4,P)=21 010 01001 其中卫,为系数矩阵A第j列的向量.A的秩为3,方程 组变量个数大于A的秩,从方程组的无数组解中找一 个初始可行解
§ 1 单纯形法的基本思路和原理 该线性规划问题约束方程的系数矩阵为: 其中 pj为系数矩阵 A 第 j 列的向量.A 的秩为3,方程 组变量个数大于 A 的秩,从方程组的无数组解中找一 个初始可行解。 1 2 3 4 5 1 1 1 0 0 ( , , , , ) 2 1 0 1 0 0 1 0 0 1 A p p p p p